Принятие решений в условиях полной неопределенности

Неопределенность, связанную с отсутствием информации о вероятностях состоянии среды (природы), называют «безнадеж­ной» или «дурной».

В таких случаях для определения наилучших решении ис­пользуются следующие критерии: максимакса, Вальда, Сэвиджа, Гурвица. Альтернативные подходы, в частности принципы Байеса - Лапласа, рассматриваются в разд. 6.2.1.

Применение каждого из перечисленных критериев проиллю­стрируем на примере матрицы выигрышей (3.1) или связанной с ней матрицы рисков (3.2).

Критерий максимакса. С его помощью определяется страте­гия, максимизирующая максимальные выигрыши для каждого состояния природы. Это критерий крайнего оптимизма. Наилуч­шим признается решение, при котором достигается максималь­ный выигрыш, равный .

Нетрудно увидеть, что для матрицы А наилучшим решением будет А₁, при котором достигается максимальный выигрыш - 9.

Следует отметить, что ситуации, требующие применения такого критерия, в экономике в общем нередки, и пользуются им не только безоглядные оптимисты, но и игроки, поставленные в безвыходное положение, когда они вынуждены руководствовать­ся принципом «или пан, или пропал».

Максиминный критерий Вальда. С позиций данного крите­рия природа рассматривается как агрессивно настроенный и сознательно действующий противник типа тех, которые проти­водействуют в стратегических играх (см. гл. 2). Выбирается ре­шение, для которого достигается значение .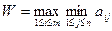

Для платежной матрицы А (3.1) нетрудно рассчитать:

• для первой стратегии (i = 1) ;

• для второй стратегии (i =2) ;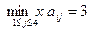

• для третьей стратегии (i =3) .

Тогда , что соответствует второй стратегии A₂ игрока 1.

В соответствии с критерием Вальда из всех самых неудач­ных результатов выбирается лучший (W = 3). Это перестрахо­вочная позиция крайнего пессимизма, рассчитанная на худший случай. Такая стратегия приемлема, например, когда игрок не столь заинтересован в крупной удаче, но хочет себя застраховать от неожиданных проигрышей. Выбор такой стратегии определя­ется отношением игрока к риску.

Критерий минимаксного риска Сэвиджа. Выбор стратегии аналогичен выбору стратегии по принципу Вальда с тем отличи­ем, что игрок руководствуется не матрицей выигрышей А (3.1), а матрицей рисков R (3.2):

Для матрицы R (3.2) нетрудно рассчитать:

• для первой стратегии (i =1) ;

• для второй стратегии (i =2) ;

• для третьей стратегии (i =3) .

Минимально возможный из самых крупных рисков, равный 4, достигается при использовании первой стратегии А₁.

Критерий пессимизма-оптимизма Гурвица. Этот критерий при выборе решения рекомендует руководствоваться некоторым сред­ним результатом, характеризующим состояние между крайним пес­симизмом и безудержным оптимизмом. Согласно этому критерию стратегия в матрице А выбирается в соответствии со значением

При p = 0 критерий Гурвица совпадает с максимаксным кри­терием, а при р = 1 - с критерием Вальда. Покажем процедуру применения данного критерия для матрицы А (3.1) при р = 0,5:

• для первой стратегии

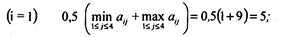
• для второй стратегии

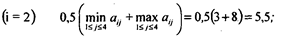
• для третьей стратегии

 

Тогда , т.е. оптимальной является вторая стратегия А₂.

Применительно к матрице рисков R критерий пессимизма-оптимизма Гурвица имеет вид:

При р = 0 выбор стратегии игрока 1 осуществляется по ус­ловию наименьшего из всех возможных рисков ( ); при р = 1 - по критерию минимаксного риска Сэвиджа.

В случае, когда по принятому критерию рекомендуется к использованию несколько стратегий, выбор между ними может делаться по дополнительному критерию, например в расчет могут приниматься средние квадратичные отклонения от средних вы­игрышей при каждой стратегии. Данная идея отвечает подходу, рассмотренному в разд.1.2 (см. рис. 1.1). Еще раз подчеркнем, что здесь стандартного подхода нет. Выбор может зависеть от склонности к риску ЛПР.

В заключение приведем результаты применения рассмотрен­ных выше критериев на примере следующей матрицы выигры­шей:

Для игрока 1 лучшими являются стратегии:

• по критерию Вальда – А₃,

• по критерию Сэвиджа – А₂ и А₃,

• по критерию Гурвица (при р = 0,6) – А₃;

• по критерию максимакса – А₄.

Поскольку стратегия А₃, фигурирует в качестве оптимальной по трем критериям выбора из четырех испытанных, степень ее надежности можно признать достаточно высокой для того, что­бы рекомендовать эту стратегию к практическому применению.

Таким образом, в случае отсутствия информации о вероят­ностях состоянии среды теория не дает однозначных и матема­тически строгих рекомендации по выбору критериев принятия решений. Это объясняется в большей мере не слабостью тео­рии, а неопределенностью самой ситуации. Единственный ра­зумный выход в подобных случаях - попытаться получить до­полнительную информацию, например, путем проведения ис­следований или экспериментов. В отсутствие дополнительной информации принимаемые решения теоретически недостаточ­но обоснованы и в значительной мере субъективны. Хотя при­менение математических методов в играх с природой не дает абсолютно достоверного результата и последний в определен­ной степени является субъективным (вследствие произвольно­сти выбора критерия принятия решения), оно тем не менее создает некоторое упорядочение имеющихся в распоряжении ЛПР данных: задаются множество состояний природы, альтер­нативные решения, выигрыши и потери при различных сочета­ниях состояния «среда - решение». Такое упорядочение пред­ставлений о проблеме само по себе способствует повышению качества принимаемых решений.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: