Пересечение поверхностей многогранников

При пересечении двух многогранников линия пересечения поверхностей представляет собой ломаную линию.

Если ребра двух призм взаимно перпендикуляр­ны (рис. 62, а), то линия пересечения призм строится следующим образом.

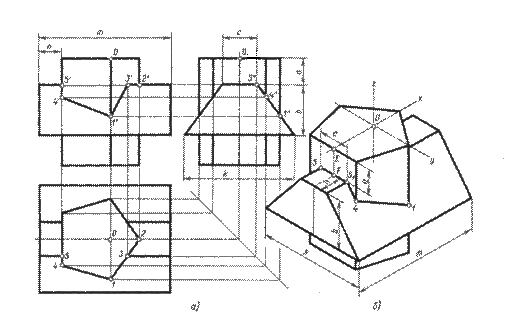
Рис. 62

Горизонтальная и профильная проекции линии пересечения совпадают соответственно с горизон­тальной проекцией пятиугольника (основания одной призмы) и с профильной проекцией четы­рехугольника (основания другой призмы). Фрон­тальную проекцию ломаной линии пересечения строят по точкам пересечения ребер одной призмы с гранями другой.

Например, взяв горизонтальную 1 и про­фильную 1" проекции точки 1 пересечения ребра пятиугольной призмы с гранью четырех­угольной (рис. 62, а) и пользуясь известным приемом построения, с помощью линии связи можно легко найти фронтальную проекцию 1' точки 1, принадлежащей линии пересечения призм.

Изометрическая проекция двух пересекающих­ся призм (рис. 62, б) может быть построена по координатам соответствующих точек.

Например, изометрическую проекцию двух точек 5 и 5', симметрично расположенных на левой грани пятиугольной призмы, строят так. Принимая для удобства построений за начало координат точку О, лежащую на верхнем основа­нии пятиугольной призмы, откладываем влево от О по оси х отрезок ОЕ, величину которого берут с комплексного чертежа на фронтальной или го­ризонтальной проекции. Далее из точки Е вниз параллельно оси z откладываем отрезок EF, рав­ный а, и, наконец, от точки F влево и вправо параллельно оси у откладываем отрезки F5 и F5', равные с/2.

Далее от точки F параллельно оси х откладыва­ем отрезок п, взятый с комплексного чертежа. Через его конец проводим прямую, параллельную оси у, и откладываем на ней отрезок, равный с. Вниз параллельно оси z откладываем отрезок, равный b, и параллельно у — отрезок, равный к.

В результате получаем изометрию основания че­тырехугольной призмы.

Точки 1 и 4 на ребрах пятиугольной призмы можно построить, используя только одну коорди­нату z.

Линию пересечения поверхностей четыреху­гольной призмы с четырехугольной пирамидой (рис. 63, а) строят по точкам пересечения ребер одного многогранника с гранями другого многог­ранника.

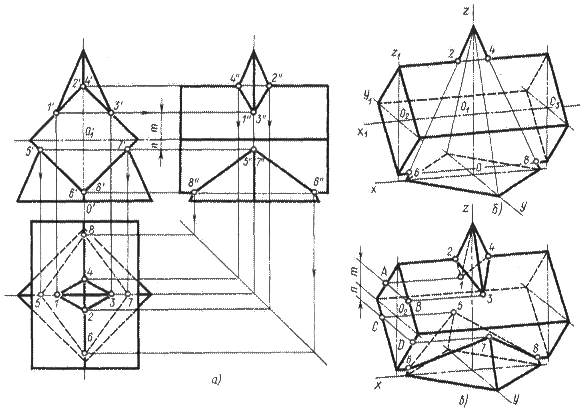
Рис. 63

Например, проекции точек 1 и 3 искомой ли­нии пересечения находят следующим образом. Фронтальные проекции 1' и 3' очевидны. Про­фильные проекции 1" и 3" и горизонтальные 1 и 3 находят с помощью линий связи. Аналогично находят точки 2 и 4.

На рис. 63, б и в показана последовательность построения диметрической проекции. Сначала строят пирамиду. Для построения призмы от точ­ки О откладывают отрезок OO₁, взятый с фрон­тальной проекции комплексного чертежа (О'О'₁ ), и получают точку О₁ (рис. 63, б). Через точку O₁  проводят параллельно оси х ось симметрии призмы и по ней от точки O₁ откладывают вправо и влево половины высоты призмы. Через точки О₂ и О₃ проводят прямые, параллельные осям у и z, на которых откладывают соответственно половину и целую длину диагоналей четырехугольника основания призмы. Соединив концы диагоналей прямыми, получают диметрическую проекцию основания призмы.

Диметрические проекции точек пересечения 2, 4, 6, 8 ребер призмы и пирамиды получаются без дополнительных построений (рис. 63, в).

Диметрические проекции точек пересечения 1, 3, 5, 7 ребер пирамиды с гранями призмы находят по координатам известным способом.

В этом примере диметрические проекции точек 1, 3, 5 и 7 можно построить иначе. От середины левого основания призмы — точки О₂ — отклады­ваем вверх и вниз по оси z соответственно отрезки m и п, взятые с комплексного чертежа. Через концы отрезков т и п проводят прямые, парал­лельные оси у, до пересечения с контуром основа­ния призмы в точках А, В, С и D. Через эти точ­ки проводят прямые, параллельные оси х, до пе­ресечения с ребрами пирамиды. В результате по­лучают искомые точки 1, 3, 5 и 7.