Способы построения проекций точек пересечения прямой линии с многогранниками и кривыми поверхностями

СПОСОБЫ ПОСТРОЕНИЯ ПРОЕКЦИЙ ТОЧЕК ПЕРЕСЕЧЕНИЯ ПРЯМОЙ ЛИНИИ С МНОГОГРАННИКАМИ И КРИВЫМИ ПОВЕРХНОСТЯМИ

При выполнении чертежей часто приходится решать задачи на по­строение точек пересечения прямой линии с поверхностью геометриче­ского тела.

Пусть требуется построить проек­ции точек пересечения фронтальной прямой F с поверхностью треуголь­ной призмы (рис. 51).

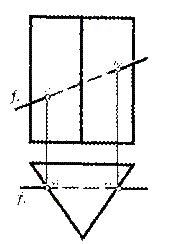
Рис. 51

Боковая поверхность призмы — проецирующая и перпендикулярна к горизонтальной плоскости проек­ции П₁. Поэтому горизонтальные проекции точек, в которых прямая F(f_1, f₂) пересекает многогранник, на горизонтальной проекции призмы уже имеются. Они будут совпадать с проекциями тех граней призмы, в которых лежат. Отмечаем  горизон­тальные проекции а₁ и b₁ точек А и В и с помощью линий связи находим их фронтальные проекции а₂ и b_2. На чертеже линии обведены с уче­том видимости отдельных участков прямой.

На рис. 52 показан пример по­строения точек пересечения прямой общего положения L с поверхностью призмы на полном изображении.

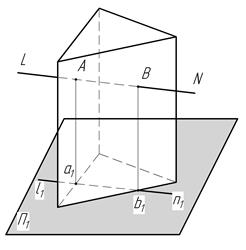
Рис. 52

Аналогично строят точки пересе­чения прямой L с поверхностью ци­линдра (рис. 53).

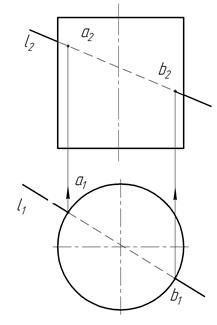
Рис. 53

В случае пересечения прямой с поверхностями пирамиды (рис. 54), конуса и другими, которые не явля­ются проецирующими, поступают так.

 

Рис. 54

Через заданную прямую прово­дят вспомогательную проецирую­щую плоскость, например фронталь­но-проецирующую, и находят линию пересечения заданной поверхности с этой плоскостью.

Фронтальная проекция вспомога­тельной плоскости Р и заданной ли­нии F(f_1, f₂) на чертеже (рис. 55) совпадают.

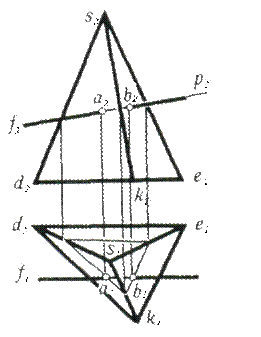
Рис. 55

 Совпадает с ними в пре­делах очерка поверхности и проек­ция линии сечения. Находят гори­зонтальную проекцию линии сече­ния. В данном случае это треугольник. В том месте, где стороны тря угольника пересекают горизонтальную проекцию f₁ заданной линии, будут находиться горизонтальные проекции а₁ и b₁ точек А и В пересечения прямой F с поверхностью пирамиды.  Точка А принадлежит грани DSK, а точка В — грани KSE. По горизон­тальным проекциям а₁ и b₁ точек на ходят фронтальные — а₂ и b₂.

Если нужно определить точки пересечения прямой с поверхностью конуса (рис. 56), сферы (рис. 57), поступают аналогично.

 

   

      

 

 

 

  

 

 

 

          

 

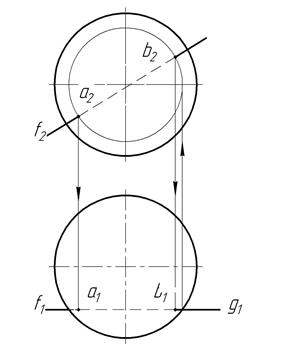
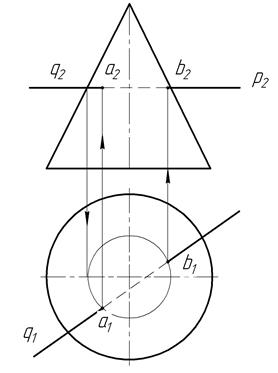
          Рис. 56                                                           Рис. 57           

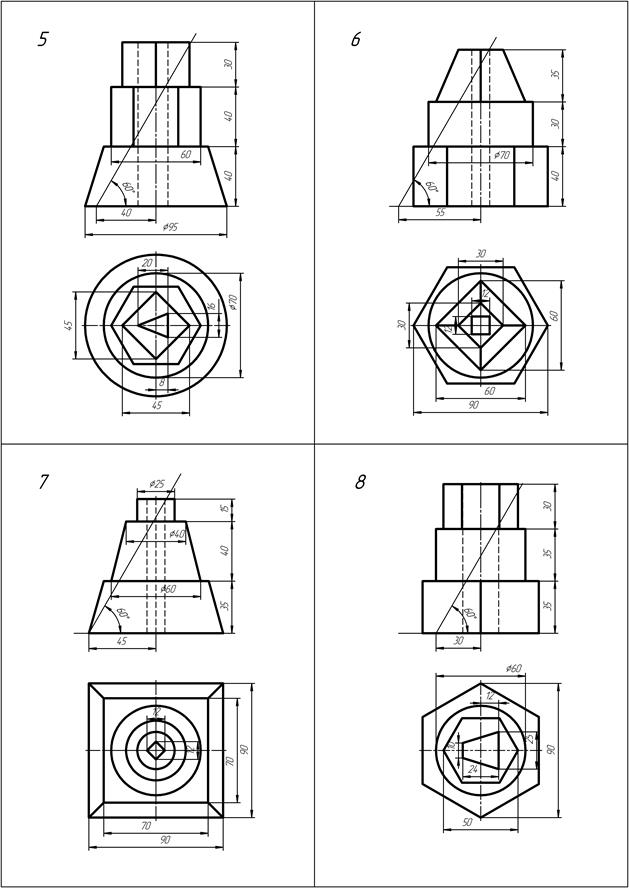
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 3 (лист 5)

Выполнить графическую работу на формате А3 по представленному образцу на рис. 58. Варианты заданий даны на (стр. 55-57).

 

	Рис. 58

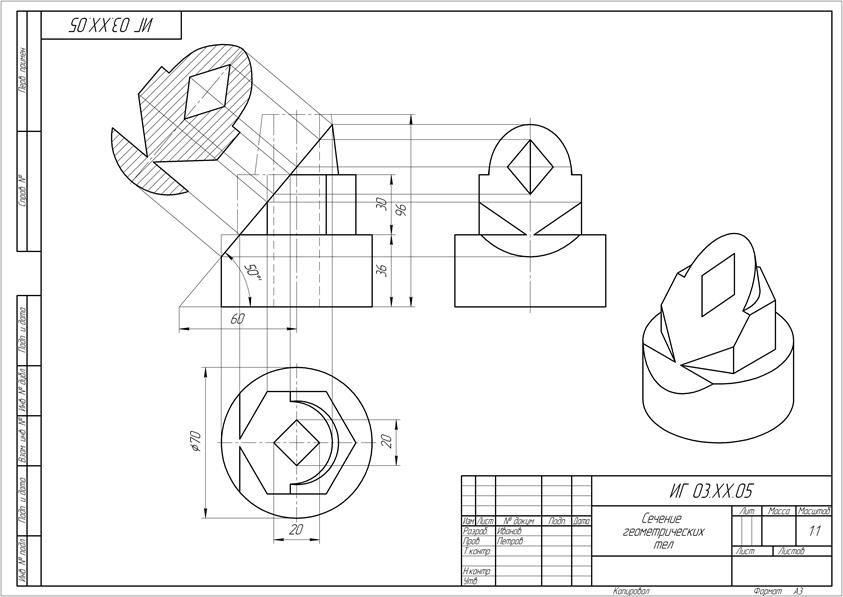
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ К РГР № 3

 

 

 

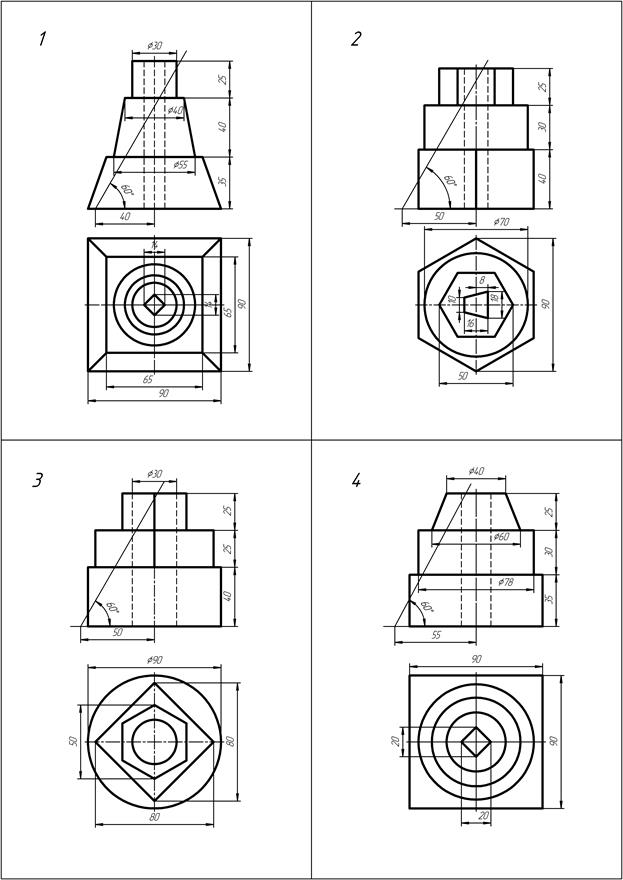
ОБЩИЕ ПРАВИЛА ПОСТРОЕНИЯ ЛИНИЙ

ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ

 

Метод построения линий пересечения повер­хностей тел заключается в проведении вспомога­тельных секущих плоскостей и нахождении от­дельных точек линий пересечения данных повер­хностей в этих плоскостях.

Построение линии пересечения поверхностей тел начинают с нахождения очевидных точек. Например, на рис. 59, где изображены линии пересечения призмы с конусом, такими точками являются точки  А и В. Затем определяют харак­терные точки, расположенные, например, на очерковых образующих поверхностей вращения или крайних ребрах, отделяющих видимую часть линий перехода от невидимой. На рис. 59 это точки С и D. Они располагаются на крайних реб­рах верхней горизонтальной грани призмы.

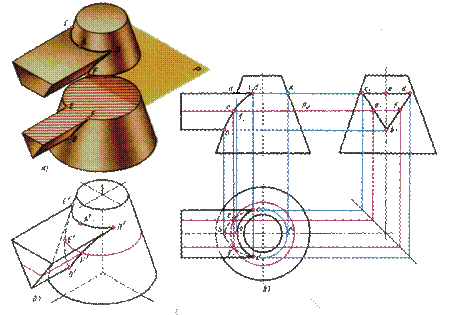
Рис. 59

Все остальные точки линии пересечения назы­ваются промежуточными (например, точки Е и F). Обычно их определяют с помощью вспомога­тельных параллельных секущих плоскостей (рис. 59, а).

В качестве вспомогательных плоскостей выби­рают такие плоскости, которые пересекают обе заданные поверхности по простым линиям — пря­мым или окружностям, причем окружности до­лжны располагаться в плоскостях, параллельных плоскостям проекций.

В данном примере плоскость Р рассекает конус по окружности (рис. 59, в), с помощью которой находят горизонтальные проекции точек e₁ и f₁.

Во всех случаях, перед тем как строить линию пересечения поверхностей на чертеже, необходи­мо представить себе эту линию в пространстве (рис. 59, б).

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: