Кривые поверхности. Построение проекций линии сече­ния цилиндра плоскостью. Построение проекций линии сече­ния конуса плоскостью

Кривые поверхности

Построение проекций линии сече­ния цилиндра плоскостью

При пере­сечении цилиндра вращения плос­костью, параллельной оси вращения, получается пара прямых (рис. 46, а). Если секущая плоскость пер­пендикулярна к оси вращения, в ре­зультате сечения цилиндра этой плоскостью получится окружность (рис. 46, б). В общем случае, когда секущая плоскость наклонена к оси вращения цилиндра, в сечении полу­чается эллипс (рис. 47).

 

 

 

 

 

 

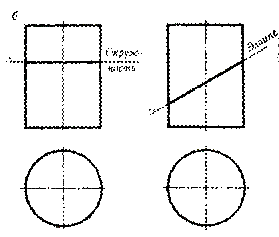
                                     Рис. 46                                     Рис. 47                                               

На рис. 48 показано построение проекций линии сечения цилиндра фронтально-проецирующей плос­костью Q (q₂) когда в сечении полу­чается эллипс.

Рис. 48

Фронтальная проекция линии се­чения в этом случае совпадает с фронтальной проекцией q₂  плоско­сти, а горизонтальная — с горизон­тальной проекцией боковой поверх­ности цилиндра. Профильная проек­ция линии строится по двум имею­щимся проекциям — горизонтальной и фронтальной. Чтобы облегчить по­строение, можно провести на поверх­ности цилиндра несколько образую­щих. Для этого делят его горизон­тальную проекцию на несколько час­тей. Затем с помощью линий связи находят фронтальные и профильные проекции образующих. Проекции то­чек, принадлежащих линии сечения, переносят при помощи линий связи с фронтальной проекции на соответствующие проекции образующих. Через найденные точки по лекалу проводят кривую линию. На черте­же должно быть найдено такое ко­личество точек, принадлежащих ли­нии сечения, чтобы точнее построить эту кривую линию.

 

Построение проекций линии сече­ния конуса плоскостью

 В зависимо­сти от направления секущей плоско­сти в сечении конуса вращения мо­гут получиться различные линии, на­зываемые линиями конических сече­ний.

Так, если секущая плоскость про­ходит через вершину конуса, в его сечении получается пара прямых (рис. 49, а).

Рис. 49

 В результате пересече­ния конуса плоскостью, перпендикулярной к оси конуса, получается окружность (рис. 49, б). Если се­кущая плоскость наклонена к оси вращения конуса и не проходит че­рез его вершину, в сечении конуса могут получиться эллипс, парабола или гипербола (рис. 49, в, г и д), в зависимости от величины угла наклона секущей плоскости к оси конуса.

Эллипс получается в том случае, когда угол 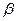 между секущей плос­костью Р(р₂) и осью вращения боль­ше, чем угол  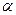между осью вращения и образующей конуса (рис. 49, в), т. е. когда плоскость пересекает все образующие данного конуса.

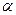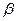Если углы и  равны, т. е. секу­щая плоскость параллельна одной из образующих конуса, в сечении получается парабола (рис. 49, г). В этом случае секущая плоскость Р(р₂) пересекает все образующие, кроме одной, которой она парал­лельна.

Если секущая плоскость Р(р₂), направленная под углом к оси вра­щения конуса, пересечет его так, что угол 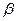 будет меньше угла 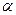, то в се­чении получится гипербола (рис. 49, д). В этом случае секущая плос­кость параллельна двум образую­щим конуса. Гипербола имеет две ветви, так как коническая поверх­ность двуполостная. Как кривая конического сечения, гипербола по­лучается и в частном случае при Р = 0, когда секущая плоскость Р(р₂) параллельна оси конуса.

На рис. 50  дано построение про­екций линии сечения конуса фрон­тально-проецирующей плоскостью Р, когда в сечении получается эл­липс.

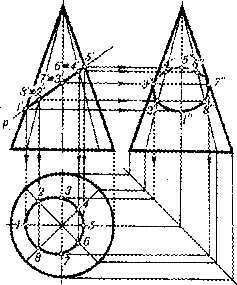
Рис. 50

Фронтальная проекция линии се­чения совпадает с фронтальной про­екцией р₂ плоскости. Две другие про­екции линии сечения находят с по­мощью линий связи. Для этого не­обходимо сначала разделить окруж­ность основания конуса на произ­вольное число равных частей (на чертеже она разделена на восемь) и провести образующие на всех трех проекциях конуса. Проекции точек линии сечения находятся на соответ­ствующих проекциях образующих. Построенные точки соединяют по лекалу.

 

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: