 |
Проекции конуса. Проекции шара
|
|
|
|
ПРОЕКЦИИ КОНУСА
Наглядное изображение прямого кругового конуса показано на рис. 39, а. Боковая поверхность конуса получена вращением отрезка BS вокруг оси, пересекающей отрезок в точке S. Последовательность построения двух проекций конуса показана на рис. 39, б и в.

Рис. 39
Сначала строят две проекции основания. Горизонтальная проекция основания — окружность. Фронтальной проекцией будет отрезок горизонтальной прямой, равный диаметру этой окружности (рис. 39, б). На фронтальной проекции из середины основания восставляют перпендикуляр и на нем откладывают высоту конуса (рис. 39, в). Полученную фронтальную проекцию вершины конуса соединяют прямыми с концами фронтальной проекции основания и получают фронтальную проекцию конуса.
Если на поверхности конуса задана одна проекция точки А (например, фронтальная проекция на рис. 40, а), то две другие проекции этой точки определяют с помощью вспомогательных линий — образующей, расположенной на поверхности конуса и проведенной через точку А, или окружности, расположенной в плоскости, параллельной основанию конуса.
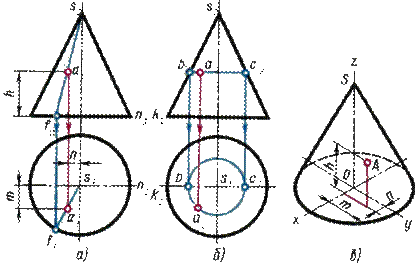
Рис. 40
В первом случае (рис. 40, а) проводят фронтальную проекцию s2a2f2 вспомогательной образующей. Пользуясь вертикальной линией связи, проведенной из точки f2, расположенной на фронтальной проекции окружности основания, находят горизонтальную проекцию s1f1 этой образующей, на которой с помощью линии связи, проходящей через а2, находят искомую точку а1.
Во втором случае (рис. 40, б) вспомогательной линией, проходящей через точку А, будет окружность, расположенная на конической поверхности и параллельная плоскости П1. Фронтальная проекция этой окружности изображается в виде отрезка b2с2 горизонтальной прямой, величина которого равна диаметру вспомогательной окружности. Искомая горизонтальная проекция а1 точки А находится на пересечении линии связи, опущенной из точки а2, с горизонтальной проекцией вспомогательной окружности.
|
|
|
Если заданная фронтальная проекция b2 точки В расположена на контурной (очерковой) образующей SK, то горизонтальная проекция точки находится без вспомогательных линий (рис. 40, б).
В изометрической проекции точку А, находящуюся на поверхности конуса, строят по трем координатам (рис. 40, в): хА = n, уА = m, zA = h. Эти координаты последовательно откладывают по направлениям, параллельным изометрическим осям. В рассматриваемом примере от точки О по оси х отложена координата хa = n; из конца ее параллельно оси у проведена прямая, на которой отложена координата уА = m; из конца отрезка, равного m, параллельно оси z проведена прямая, на которой отложена координата zA = h. В результате построений получим искомую точку А.
ПРОЕКЦИИ ШАРА
На рис. 41, а изображена половина шара, сферическая поверхность этого шара образована вращением четверти окружности АВ вокруг радиуса АО.
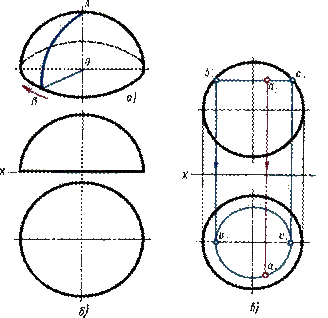
Рис. 41
Проекции этой фигуры приведены на рис. 41, б. Горизонтальная проекция — окружность радиуса, равного радиусу сферы, а фронтальная — полуокружность того же радиуса.
Если точка А расположена на сферической поверхности (рис. 41, в), то вспомогательная линия b2с2, проведенная через эту точку параллельно горизонтальной плоскости проекций, проецируется на горизонтальную плоскость проекций окружностью. На горизонтальной проекции вспомогательной окружности находят с помощью линии связи искомую горизонтальную проекцию а1 точки А.
Величина диаметра вспомогательной окружности равна фронтальной проекции b2с2.
На практике часто приходится выполнять чертежи деталей, форма которых представляет собой геометрическое тело, усеченное одной или несколькими плоскостями. Условное рассечение предмета используется также для выявления его геометрической формы и внутреннего очертания.
|
|
|
|
|
|


