Общие сведения о пересечении поверхности плоскостью

ОБЩИЕ СВЕДЕНИЯ О ПЕРЕСЕЧЕНИИ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ

При пересечении любого тела с плоскостью получается некоторого вида плоская фигура, называемая сечением. Под сечением понимают ту часть секущей плоскости, кото­рая находится внутри рассеченного тела и ограничена линией сечения. Линией сечения тела плоскостью яв­ляется контур этого сечения.

Плоскости, с помощью которых получается сечение, называют секу­щими.

Фигура сечения многогранника — многоугольник, число сторон которо­го равно числу граней, пересекаемых плоскостью. Вершинами этого мно­гоугольника являются точки пере­сечения ребер с секущей плоскостью, а сторонами — линии пересечения граней с секущей плоскостью. Плос­кие сечения многогранников — зам­кнутые фигуры.

В пересечении кривой поверхности плоскостью в общем случае получа­ется плоская кривая линия (окруж­ность, эллипс и т. п. ). При пересе­чении линейчатых поверхностей плоскостями могут получаться, в частности, и прямые линии, если се­кущая плоскость направлена вдоль образующих (цилиндра, конуса и др. ).

Основным способом построения точек линии пересечения поверхно­сти с плоскостью является способ вспомогательных секущих плоскостей. Вспомогательная плоскость пересекает секущую плос­кость по прямой, а заданную поверх­ность по некоторой кривой или пря­мой линии. Точки пересечения этих линий и будут искомыми точками, принадлежащими поверхности и се­кущей плоскости.

Построение проекций линии сече­ния поверхности плоскостью значи­тельно упрощается, если секущая плоскость проецирующая. В этом случае одна из проекций линии сече­ния уже имеется на чертеже: она совпадает с проекцией плоскости. Остается лишь найти другие проек­ции этой линии.

 

ПОСТРОЕНИЕ ЧЕРТЕЖЕЙ МНОГОГРАННИКОВ

 И КРИВЫХ ПОВЕРХНОСТЕЙ, ПЕРЕСЕЧЕННЫХ ПРОЕЦИРУЮЩЕЙ ПЛОСКОСТЬЮ

Многогранники

Как было уже указано, в сечении многогранника плоскостью получается многоугольник.

 Его можно построить двумя способами.

Первый способ. Находят вершины многоугольника как точки пересечения ребер многогранника с секущей плоскостью.

Второй способ. Находят сто­роны многоугольника как линии пе­ресечения граней многогранника с секущей плоскостью.

Построение проекций линии сече­ния призмы плоскостью. На рис. 42 показано построение проекций линии сечения прямой пятиугольной приз­мы фронтально-проецирующей плос­костью Р.

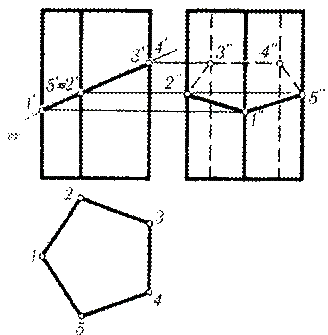
Рис. 42

Фронтальная проекция линии сече­ния совпадает с фронтальной проек­цией р₂ секущей плоскости, а горизонтальная — с горизонтальной проекцией боковой поверхности приз­мы. Профильная проекция линии сечения находится с помощью линий связи, проведенных из точек 1', 2', 3', 4' и 5' до пересечения с профильными проекциями соответствующих ребер призмы в точках 1", 2", 3", 4" и 5" . На рис. 42 линия сечения показана с учетом видимости ее отдельных частей.

На рис. 43 изображена усеченная часть призмы, оставшаяся после сечения геометрического тела плоскостью и удаления верхней отсеченной части.

 

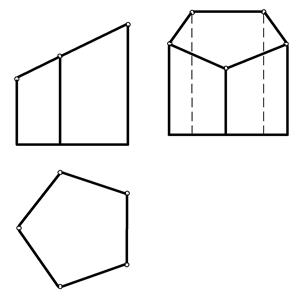
Рис. 43

 

Построение проекций линии сечения пирамиды плоскостью

На рис. 44 в наглядном изображении показано сечение пирамиды секущей плоскостью, а на рис. 45 показана схема построения фигуры сечения треугольной пирамиды фронтально-проецирующей плоскостью Р.

            

 

              

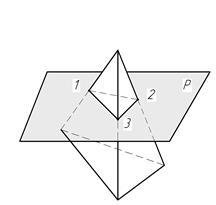
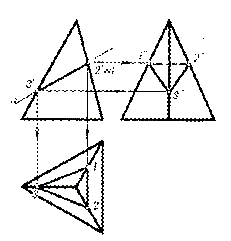
                      Рис. 44                                               Рис. 45

Фронтальная проекция линии сечения совпадает с фронтальной проекцией р₂ плоскости. Горизонтальные и профильные проекции точек принадлежащих линии сечения, находят с помощью линий связи, проведенных из точек 1', 2' и 3' до пересечения их с горизонтальными и  профильными проекциями ребер (рис. 45). Последовательность построения этих проекций точек чертеже пирамиды показана стрелками.

 

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: