 |
Классическое определение вероятности события. Геометрическая вероятность.
|
|
|
|
Вопросы контроля
1. Определение случайного события. Пример.
2. Определение достоверного и невозможного события. Пример.
3. Определение несовместных событий. Пример.
4. Определение полной группы событий. Пример.
5. Определение суммы двух событий. Пример.
6. Определение произведения событий. Пример
7. Определение противоположных событий. Пример
8. Определение частоты события, ее свойства.
9. Статистическое определение вероятности события его достоинства и недостатки.
10. Классическое определение вероятности события, его достоинства и недостатки.
11. Геометрическая вероятность события.
Задачи
1. Образуют ли полную группу события, какие являются равновозможными, несовместными?
· Опыт: бросание двух правильных монет. а) А – выпадение двух гербов, В – выпадение двух цифр; б) С – на первой монете выпадение герба, D – на второй монете выпадение цифры; в) E – выпадение одного герба, F – выпадение одной цифры.
· Опыт: извлечение двух карт из колоды игральных карт. а) А – обе карты червы, В – одна из карт туз; б) С – одна из карт девятка, D – вторая карта не девятка.
· Опыт: возможное совершение покупки двумя покупателями. а) А – хотя бы один покупатель совершил покупку, В – ни один из покупателей не совершил покупки; б) С – совершена ровно одна покупка, В – произведено две покупки.
2. Сколько четырехбуквенных слов (слово – произвольный набор букв) можно образовать из букв слова "сапфир"? Сколько из них не содержат буквы "р"? Сколько таких, которые начинаются с буквы "с" и оканчиваются буквой "р"?
3. Сколько пятибуквенных слов, каждое из которых содержит 2 гласные и 3 согласные можно образовать из букв слова "сочетание"?
|
|
|
4. Предприятие может предоставить работу по одной специальности четырем женщинам, по другой специальности – пяти мужчинам и по третьей специальности – трем работникам независимо от их пола. Сколькими способами можно заполнить эти места, если имеется 18 претендентов, среди которых 8 женщин и 10 мужчин?
5. Какое число различных парных нарядов можно назначить из бригады в 12 человек? Сколькими способами можно составить такой наряд, если один из двух членов бригады должен быть назначен старшим?
6. Сколько различных линий можно провести через 8 точек, из которых никакие три не лежат на одной прямой?
7. Имеется три различных флага. На флагштоке поднимается сигнал, состоящий не менее чем из двух флагов. Сколько различных сигналов можно поднять на флагштоке (порядок флагов учитывается)?
8. Пассажирский поезд состоит из двух багажных вагонов, четырех плацкартных и трех купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале, а купированные – в конце.
9. Позывные радиостанции должны начинаться с буквы 
. Скольким радиостанциям можно присвоить различные позывные, если позывные состоят: а) из трех букв, причем эти буквы могут повторяться; б) из четырех различных букв?
10. Сколько различных перестановок можно образовать из всех букв слова "Миссисипи"?
11. Кубик, все грани которого окрашены, распилен на 1000 кубиков одинакового размера. Полученные кубики тщательно перемешаны. Определить вероятность того, что наудачу извлеченный кубик будет иметь ровно две окрашенные грани, три окрашенные грани.
12. На карточках написаны буквы: «а», «е», «к», «р». Карточки перемешиваются и раскладываются в ряд. Какова вероятность того, что получится слово «река»?
13. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
|
|
|
14. Подсчитать вероятность того, что в наудачу выбранном телефонном номере, состоящем из 4 цифр, все цифры окажутся различными? (Предполагается наличие произвольного номера, в частности 0000.)
15. Из 30 экзаменационных билетов наудачу извлекается один. Какова вероятность того, что номер вытянутого билета есть число, кратное пяти?
16. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором 3 вопроса.
17. Группа студентов из 15 юношей и 5 девушек выбирает по жребию хозяйственную команду в составе четырех человек. Какова вероятность того, что в составе этой команды окажутся два юноши и две девушки?
18. Из 33 карточек с буквами русского алфавита наудачу выбирается пять. Какова вероятность, что из них можно составить слово "буква"?
19. 
человек рассаживаются в ряд в случайном порядке. Какова вероятность, что два определенных лица окажутся рядом? Найти соответствующую вероятность, если те же лица садятся за круглый стол (места за круглым столом пронумерованы).
20. Найдите вероятность того, что наудачу выбранное двузначное число не содержит ни одной двойки
21. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди извлеченных деталей: а) нет бракованных; б) нет годных; в) ровно 3 годных.
22. Из тщательно перемешанного полного набора 28 костей домино наудачу извлечена кость. Найти вероятность того, что вторую наудачу извлеченную кость можно приставить к первой, если: а) первая кость оказалась дублем; б) первая кость – не дубль.
23. Устройство состоит из пяти элементов, из которых 2 изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.
24. Точка брошена наудачу внутрь круга радиуса 
. Какова вероятность того, что расстояние точки от центра круга окажется меньше 
?
25. Плоскость разграфлена параллельными прямыми, находящимися друг от друга на расстоянии 
. На плоскость наудачу брошена монета радиуса 
. Найти вероятность того, что монета не пересечёт ни одной из прямых.
26. Какова вероятность того, что сумма двух наугад взятых положительных чисел, каждое из которых не больше 1, не превзойдет единицы, а их произведение будет не больше 
?
|
|
|
27. Два студента условились встретиться в определенном месте между 12 и 13 часами дня. Пришедший первым ждет второго в течении 1/3 часа, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода (в промежутке от 12 до 13 часов).
28. Наудачу взяты два положительных числа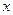 
и 
, каждое из которых не превышает двух. Найти вероятность того, что произведение 
будет не больше 
, а частное 
не больше 2.
|
|
|
