Аксиоматика Колмогорова. Теоремы сложения и умножения.

Вопросы контроля

1. Аксиоматическое построение вероятности события

2. Теорема сложения

3. Условная вероятность события

4. Теорема произведения

Задачи

1. Покупатель проходит мимо трех расположенных подряд стеллажей с товарами и совершает или не совершает покупку. Вероятность покупки товара на первом стеллаже 0,7 и уменьшается на 0,1 при каждом последующем стеллаже. Какова вероятность получить ровно две покупки?

2. Вероятность совершения покупки первым покупателем равна 0,7, а вторым – 0,8. Какова вероятность того, что будет совершена хотя бы одна покупка, если они совершаются независимо друг от друга?

3. Устройство состоит из трех элементов, работающих независимо. Вероятность безотказной работы (за время ) первого, второго и третьего элементов соответственно равны 0,6, 0,7 и 0,8. Найти вероятность того, что за время безотказно будут работать: а) только один элемент; б) только два элемента; в) все три элемента.

4. В урне 5 белых и 4 черных шара. Из нее вынимаются подряд два шара. Найти вероятность того, что оба шара белые.

5. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.

6. Брошены три игральные кости. Найти вероятности следующих событий: а) на каждой из выпавших граней появится пять очков; б) на всех выпавших гранях появится одинаковое число очков.

7. Имеется две урны, в первой 2 белых и 3 черных шара, во второй – 4 белых и 2 черных. Из каждой урны вынимается по одному шару. Найти вероятность того, что шары будут: а) одного и того же цвета; б) разного цвета.

8. В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятность отказов первого, второго и третьего элементов соответственно равны . Найти вероятность того, что сигнал цепь а) пройдет, б) не пройдет.

9. По каналу связи передается 5 сообщений. Каждое из них (независимо от других) с вероятностью 0,2 искажается. Найти вероятность следующих событий: а) 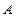– все сообщения переданы без искажений; б) – все сообщения будут искажены; в) 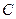– не менее двух сообщений будет искажено.

10. Реклама растворимого кофе «Гранд» предается по каналам ОРТ, РТР, НТВ. Вероятность того, что потребитель увидит эту рекламу на канале ОРТ, равна 0,1; на РТР - 0,15 и на канале НТВ – 0,05. Найти вероятность того, что потребитель увидит эту рекламу: а) по всем трем каналам; б) хотя бы по одному из этих каналов.

11. Аналитики торговой компании считают, что покупатели, обладающие дисконтной картой этой компании, обратятся в магазины этой компании с вероятностью 0,9. Если это произойдет, то покупатель совершает покупку с вероятностью 0,7. Найти вероятность того, что покупатель обладающий дисконтной картой этой компании совершит покупку.

12. В городе имеется четыре коммерческих банка, оценка надежности которых 0,95; 0,93; 0,9; 0,87 соответственно. Администрацию города интересуют ответы на вопросы: а) какова вероятность того, что в течении года обанкротятся три банка; б) хотя бы один банк.

13. Инвестор полагает, что в следующем периоде вероятность роста акций компании А будет 0,7. Вероятность того, что цены поднимутся на акции компаний А и В равна 0,28. Вероятность роста акций хотя бы одной из этих компаний равна 0,82. Найти вероятность роста акций компании В.

14. Компания имеет два независимых источника электроэнергии для использования в случае аварийного отключения постоянного источника электроэнергии. Вероятность того, что, что первый из этих резервных источников будет доступен и исправен равна 0,85; второй – 0,8. Найти вероятность того, что не произойдет отключения электроэнергии, если выйдет из строя постоянный источник.