Формула полной вероятности, асимптотические формулы

Вопросы контроля

1. Формула полной вероятности

2. Формула Байеса

3. Формула Бернулли

4. Формула наивероятнейшего числа

5. Локальная формула Лапласа

6. Интегральная формула Лапласа

7. Формула отклонения частоты от вероятности

Задачи

1. В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.

2. Имеется две партии изделий по 12 и 10 штук, причем в первой партии одно изделие бракованное, а во второй партии два изделия бракованные. Изделие, взятое наудачу из первой партии, переложено во вторую, после чего выбирается наудачу изделие из второй партии. Определить вероятность извлечения бракованного изделия из второй партии.

3. Пусть в условиях задачи 2 известно, что извлеченное из второй партии изделие – бракованное. Определить вероятность того, что при этом из первой партии было извлечено так же бракованное изделие.

4. Три станка автомата выпускают однотипные детали одного и того же количества. Вероятность появления бракованной детали для каждого станка равна 0,1, 0,05, 0,07 соответственно. Все детали произведенные станками помещаются в один ящик. Из него наудачу выбирают деталь, какова вероятность взятия стандартной детали.

5. В условиях предыдущей задачи, взятая деталь оказалась стандартной. Какова вероятность того, что ее выпустил второй станок.

6. Что вероятнее выиграть у равносильного противника: 1) три партии из четырех или пять из восьми? 2) не менее трех партий из четырех или не менее пяти партий из восьми?

7. Имеется 5 станций, с которыми поддерживается связь. Время от времени связь прерывается из-за атмосферных помех. Вследствие удаленности станций друг от друга перерыв связи с каждой из них происходит независимо от остальных с вероятностью 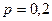. Найти вероятность того, что в данный момент времени будет иметься связь не более чем с двумя станциями.

8. Прибор состоит из 8 однородных элементов, но может работать при наличии в исправном состоянии не менее 6 из них. Каждый из элементов за время работы прибора выходит из строя независимо от других с вероятностью 0,2. Найти вероятность того, что прибор откажет за время .

9. При технологическом процессе 85% всей произведенной продукции высшего сорта. Найти наивероятнейшее число изделий высшего сорта в партии из 150 изделий.

10. Вероятность получения с конвейера изделий 1 сорта равна . Определить вероятность того, что из взятых на проверку 600 изделий 530 будут 1 сорта. Определить наивероятнейшее число изделий первого сорта.

11. Вероятность того, что деталь не прошла проверку отдела технического контроля 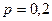. Найти вероятность того, что среди 400 случайным образом отобранных деталей окажется непроверенных от 70 до 100 деталей.

12. Вероятность производства стандартной детали равна 0,75. Найти вероятность того, что из 100 деталей стандартных будет: а) не менее 70 и не более 80 раз; б) не более 70 раз.

13. В НИИ земледелия проверяется всхожесть кукурузы. Сколько семян необходимо посеять, чтобы с вероятностью 0,99 можно было ожидать что частота всхожести отклонения от 0,95 по абсолютной величине меньше чем на 0,01?

14. Группа студентов, сдающая экзамен, состоит из 5 отличников, 10 хороших студентов и 15 слабых студентов. Отличник всегда получает оценку "отлично", хороший студент – "отлично" и "хорошо" с равными вероятностями, слабый студент – "хорошо", "удовлетворительно" и "не удовлетворительно" с равными вероятностями. Какова вероятность того, что наугад вызванный студент получил оценку: а) "отлично"; б) "хорошо"?

15. Вероятности того, что во время работы ЭВМ произойдет сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах относятся как 3:2:5. Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти, в остальных устройствах соответственно равны 0,8; 0,9; 0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен.

16. Устройство состоит из трех независимо работающих основных элементов, оно отказывает, если отказывает хотя бы один элемент. Вероятность отказа каждого элемента за время равна 0,1. Найти вероятность безотказной работы устройства за время , если а) работают только основные элементы; б) включен один резервный элемент; в) включены два резервных элемента. Предполагается, что резервные элементы работают в том же режиме, что и основные, вероятность отказа каждого резервного элемента 0,1 и устройство отказывает, если работает менее трех элементов.

17. Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна 0,8. Найти вероятность того, что событие появится: а) не менее 75 раз и не более 90 раз; б) не менее 75 раз; в) не более 74 раз.

18. Вероятность появления события в каждом из 21 независимых испытаний равна 0,7. Найти вероятность того, что событие появится в большинстве испытаний.

19. Отдел технического контроля проверяет партию из 10 деталей. Вероятность того, что деталь стандартна, равна 0,75. Найти наивероятнейшее число деталей, которые будут признаны стандартными.

20. Вероятность появления события в каждом из 900 независимых испытаний равна 0,5. Найти вероятность того, что относительная частота появления события отклоняется от его вероятности по абсолютной величине не более, чем на 0,02.

21. Вероятность того, клиент банка не вернет заем в период экономического роста, равна 0,05; в период экономического кризиса 0,15. Вероятность того, что начнется период экономического, роста равна 0,67. Найти вероятность того, что случайно выбранный клиент банка не вернет полученный кредит.

22. Психологами установлено, что мужчины и женщины по разному реагируют на жизненные обстоятельства. Исследования показали, что 70% женщин позитивно реагируют на изучаемые обстоятельства и 40% мужчин негативно реагируют на эти же обстоятельства. Произведен опрос 40 женщин и 10 мужчин. Случайно извлеченная анкета содержит негативную реакцию. Определить вероятность того, что ее заполнял мужчина.

23. Нефтеразведочная экспедиция проводит исследования для определения вероятности наличия нефти на месте предполагаемого бурения. Предыдущие исследования показали, что вероятность наличия нефти на проверяемом участке 0,45. На завершающем этапе разведки проводится сейсмический тест. Если на проверяемом участке есть нефть, то тест покажет ее наличие в 87%. Если нефти нет то тест в 8% ошибочно укажет ее наличие. Тест показал наличие нефти. Найти вероятность того, что нефть действительно присутствует на проверяемом участке.

24. Фирма собирается заключить контракт на поставку оборудования в один из заводов. Если основной конкурент фирмы не будет претендовать на заключения контракта, то вероятность получения контракта равна 0,55, в противном случае 0,25. Вероятность того, что конкурент выдвинет свои предложения по заключению контракта, равна 0,45. Определить вероятность заключения контракта фирмой.

25. Дилер, торгующий ценными бумагами, в среднем продает 70% имеющихся у его бумаг. Сколько должно быть у него ценных бумаг, что бы можно было утверждать с вероятностью 0,996, что доля проданных бумаг отклонится от70% не более чем на 0,04 (по абсолютной величине)?

 

 

Случайные величины

Вопросы контроля

1. Понятие случайной величины, дискретные, непрерывные.

2. Закон распределения, ряд распределения. Полигон, многоугольник распределения

3. Функция распределения, ее свойства

4. Плотность распределения случайной величины, ее свойства

	-2
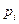
	0,1	0,3	0,4

Задачи

1. Дискретная случайная величина задана рядом распределения

Построить многоугольник распределения, функцию распределения и ее график.

2. В магазин в течении часа заходят 3 покупателя. Каждый из них совершает одну покупку с вероят­ностью 0,6;0,7;0,8 соответственно. Составить ряд распределения случайной величины выра­жающей число покупок. Построить полигон этой случайной величины, функцию распределения этой величины и ее график.

3. В лотерее из 50 билетов 4 выигрышных по 25, 50, 60 и 70 рублей. Некто покупает 4 билета. Составить ряд распределения случайной величины выражающей сумму выигрыша. Построить многоугольник распределения, функцию распределения, график функции распределения.

4. Задана непрерывная случайная величина своей функцией распределения 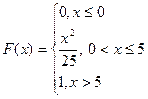. Найти плотность распределения случайной величины.

5. Непрерывная случайная величина задана плотностью распределения 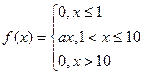. Найти параметр , интегральную функцию распределения.

6. Случайная величина задана интегральной функцией 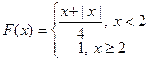. Найти дифференциальную функцию .

7. Задана плотность распределения случайной величины х: Найти: функцию распределения F(x); .

8. Случайная величина задана функцией распределения 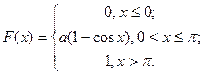Найти , .

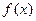9. Функция распределения случайной величины x задана выражением: Найти коэффициент , плотность вероятности 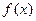и .

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: