 |
Проверка статистических гипотез
|
|
|
|
Вопросы контроля знаний
1. Определение статистической гипотезы
2. Виды гипотез
3. Определение статистического критерия
4. Определение допустимой и критической областей критерия
5. Определение ошибки первого рода. Определение уровня значимости
6. Определение ошибки второго рода. Определение мощности критерия
7. Правило отбора критерия
8. Критерии о числовых характеристиках генеральной совокупности
9. Критерии проверки равенства числовых характеристик генеральной совокупности
Решить задачи
1. Некоторая компания, производящая средства для похудания, утверждает, что при приеме ее продукции в сочетании со специальной диетой позволяет сбросить в неделю, в среднем 450 грамм. Для проведения экспертизы случайным образом отобрано 50 человек. После проведения эксперимента обнаружено, что в среднем еженедельный сброс веса составил 435 грамм, исправленное среднеквадратическое отклонение составило 135 грамм. Проверить гипотезу от том, что средняя еженедельная потеря веса составляет 450 грамм. Принять уровень значимости равный 0,01.
2. Компания по производству безалкогольных напитков предполагает выпустить на рынок новую модификацию популярного напитка, в котором сахар будет замене сукразитом. Компания хотела бы быть уверенной, что не менее 75% ее потребителей предпочтут новую модификацию напитка. Новый напиток был предложен на пробу 1000 человек, и 743 человека сказали, что новый напиток вкуснее старого. Может ли на уровне значимости 0,05 компания принять новый напиток в производство.
3. Производитель некоторой продукции утверждает, что 96% его продукции не имеют дефектов. Случайная выборка из 50 изделий показала, что 46 изделий не имеют дефектов. Проверить на уровне значимости 0,05 справедливость претензий производителя.
|
|
|
4. Компания по производству весов для торговых предприятий утверждает, что точность весов, измеряющих продукты питания весом до 10 кг, составляет 2 грамма. В торговое предприятие поступила на пробу опытная партия из 10 таких весов. По результатам взвешиваний одного продукта получили, что исправленное средне квадратическое отклонение равно 2,2 грамма. Проверить справедливость утверждения компании на уровне значимости 0,05 и 0,01.
5. В магазин поступила новая партия видеомагнитофонов. Для проверки случайным образом было отобрано 10 видеомагнитофонов. Среднее время бесперебойной работы составило 10100 часов. Средне квадратическое отклонение бесперебойной работы видеомагнитофона по данным компании производителя составляет 3000 часов. Модно ли на уровне доверия 95% принять гипотезу о том, что среднее время бесперебойной работы равно 1050 часов.
6. Фирма посредник рассылает рекламные каталоги возможным заказчикам. Как показал опыт, вероятность заказа товара, при условии получения каталога, равна 0,11. Фирма разослала 1200 каталогов новой улучшенной формы и получила 135 заказов. На уровне доверия 95% и 99% существенна ли новая форма каталога или нет.
7. Заключение страховых договоров в 150 филиалах страховых компаний составило 25000 штук в регионе А. В регионе В, в 200 филиалах составило 35000. Средне квадратические отклонения количества заключенных страховых полисов в регионах А и В, равны соответственно 10000 и 15000. Проверить на уровне значимости 0,05 существенно ли различаются регионы по количеству заключенных страховых договоров.
8. Компания по производству зубной пасты утверждает, что новый вид пасты для детей лучше, чем другие пасты. Для проверки было отобрано 450 детей, пользующиеся новой пастой и 330 детей, пользующихся другими пастами для контрольной группы. У 33 детей из опытной группы были обнаружены новые признаки кариеса, у детей из контрольной группы новые признаки кариеса обнаружены в 27 случаях. На уровне значимости 0,05 и 0,01 проверить обоснованность утверждений компании по производству нового вида зубной пасты.
|
|
|
9. Крупный коммерческий банк заказал маркетинговое исследование по выявлению эффекта «премирования» (канцелярские принадлежности) для стимула при открытии счета в банке. Для проверки случайным образом было отобрано по 150 посетителей, получивших премию и не получивших. В результате оказалось, что среди посетителей, которым не предлагалась премия 76% и среди посетителей, которым предлагалась премия, 87% открывали счета в данном банке, в течении 4 месяцев. На уровне значимости 0,05 и 0,01 проверить существенно премирование или нет.
10. Доля убыточных предприятий в 2000 году в России в среднем составила 35%. В одном из регионов России 38%. В 200 году в этой области было 8346 предприятий. На уровне значимости 0,05 и 0,01 проверить, существенны ли различия в удельном весе убыточных предприятий в данном регионе по сравнению с общероссийским или нет.
11. В 2000 году доля предприятий государственной формы собственности в одном из регионов Российской Федерации составила 3%. Среди 2500 машиностроительных и металлургических предприятий этого региона она оказалась равной 2,8%. На уровне значимости 0,05 и 0,01 проверить существенно ли различие удельного веса государственной формы собственности для всех предприятий в целом и для предприятий машиностроения и металлургии.
12. Вступительный экзамен по математике проводился на финансовом и экономическом факультетах. Среди 230 абитуриентов финансового факультета выдержало экзамен 60 человек, среди 300 абитуриентов экономического факультета выдержало экзамен 85 человек. На уровнях значимости 0,05 и 0,01 проверить, различен ли уровень подготовки абитуриентов на этих факультетах или нет.
13. Инвестиционная компания не осуществляет вложении в ценные бумаги если среднеквадратическое отклонение годового дохода более чем 0,23%. Эта компания провела 80 наблюдений по активу А и получила, что среднеквадратическое отклонение годовой доходности составило 0,24%. На уровне доверия выяснить допустимы ли вложения в актив А на уровне значимости 0,05; 0,01?
|
|
|
14. В рекламе утверждается, что средне месячный доход по акциям компании А превышает доход по акциям компании В более чем на 0,3%. В течении года средне месячный доход по акциям этих компаний составил 0,67% и 0,65% соответственно. Средне квадратические отклонения одинаковы. На уровне значимости 0,05 и 0.01 проверить справедливость рекламы.
Проверка статистических гипотез
Вопросы контроля знаний
1. Определение статистической гипотезы. Виды гипотез
2. Определение статистического критерия, допустимой и критической областей критерия
3. Определение ошибки первого рода, уровня значимости; ошибки второго рода. Определение мощности критерия
4. Правило отбора критерия, лемма Неймана-Пирсона
5. Основные типы критериев
6. Критерий согласия Пирсона
7. Критерии проверки однородности генеральных совокупностей
Решить задачи
1. Некоторое предприятие решило перейти на выпуск продукции в 2 смены. Для проверки целесообразности введения второй смены было проведено 11 обследований первой и 13 обследований второй смены на предмет средней производительности труда. Средняя производительность труда приведена в выборках. Для первой смены 33, 27, 36, 37, 39, 42, 41, 45, 43, 47, 46; для второй смены 35, 33, 31, 35, 37, 39, 37, 46, 43, 41, 43, 46, 48. Используя критерий Вилкоксона на уровне значимости 0,1проверить целесообразность введения второй смены.
2. Эффективность откорма свиней по двум рационам оценивается по выборкам объемов 9 и 13 соответственно. Первый рацион: 120,135,129,127,131,133,133,135,131. Второй рацион: 115, 125, 117, 119, 121, 125, 123, 127, 129, 127, 131, 135, 133. Используя критерий Вилкоксона на уровне значимости 0.05 проверить одинаковую эффективность этих рационов.
3. В двух городах А и Б России с одинаковым количеством жителей, провели обследование на предмет количества поездок жителями городов в общественном транспорте. В первом городе было опрошено 25 человек. Во втором 30. Получены результаты город А: 73, 32, 31, 30, 25, 26, 27, 12, 14, 15, 18, 21, 35, 38, 41, 42, 46, 48, 61, 59, 58, 57, 75, 65, 68. Город В: 29, 25, 23, 27, 19, 21, 16, 13, 11, 15, 23, 24, 32, 34, 33, 36, 35, 38, 37, 40, 39, 45, 47, 56, 58, 65, 75, 73, 71. В городе А решили увеличить парк общественного транспорта по сравнению с городом В. На уровне значимости 0.05 проверить целесообразность увеличения парк общественного транспорта с помощью критерия Вилкоксона.
|
|
|
4. В течении недели на бирже присутствовало 400 инвесторов. Известно количество совершенных ими сделок. Результаты приведены в таблице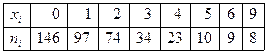 
. На уровне значимости 0,05 проверить гипотезу о том, что количество сделок имеет закон распределения Пуассона.
5. Имеется выборка из 80 значений некоторого показателя качества продукции выпускаемой фирмой.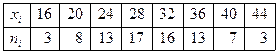 
. На уровне значимости 0,05 проверить гипотезу о нормальности распределение рассматриваемого признака качества
6. В течение минуты каждую секунду регистрировалось число попавших в счетчик Гейгера частиц. Проверить с уровнем значимости 
гипотезу о том, что число регистрируемых ежесекундно счетчиком Гейгера частиц имеет распределение Пуассона с параметром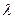 
, равным выборочному среднему. 
.
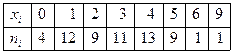7. В течении рабочего дня произведено 100 наблюдений за рабочими одного предприятия. Подсчитано количество бракованных деталей, произведенных каждым рабочим. Результаты записаны в таблице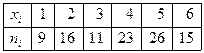 
. Проверить с уровнем значимости 
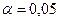гипотезу о том, что количество бракованных деталей имеет распределение: 
.
|
|
|
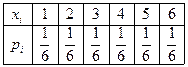