 |
Правила действий с обыкновенными дробями.
|
|
|
|
Пирютко О.Н.
Ошибки на экзаменах по математике
Оглавление
Предисловие. 3
Раздел 1. 4
Вычислительные ошибки. 4
Раздел 2. 26
Ошибки в тождественных преобразованиях. 26
Раздел 3. 35
Ошибки при решении уравнений. 35
Раздел 4. 64
Ошибки при решении неравенств. 64
Раздел 5. 93
Функции и их свойства. 93
Раздел 6. 108
Логические ошибки. 108
Раздел 7. 114
Рациональные решения. 114
Раздел 8. 154
Задания тестов. 154
Предисловие
Книга адресована школьникам для подготовки к конкурсным экзаменам.
В ней классифицированы ошибки, которые допускают абитуриенты на вступительных экзаменах в Вузы, указаны причины таких ошибок, приведена теория и алгоритмы, исключающие возможность их появления.
Книга ориентирована на школьников различных уровней подготовленности.
В первых пяти главах рассматриваются как грубые ошибки, которые допускаются при слабой подготовленности абитуриентов, так и ошибки, которые могут допустить школьники с высокими оценками по математике в экзаменационных заданиях.
Как правило, такие ошибки допускаются в заданиях, которых нет в школьных учебниках, но для их решения нужны только знания школьной программы.
Кроме того, в книге уделено внимание особенностям подготовки к тестам. В разделе «Рациональные решения» предлагаются приемы решения задач, которые способствуют успешному решению тестовых заданий.
Задачи этого раздела решены несколькими способами, среди которых и наиболее короткие и рациональные, знание методов таких решений особенного актуально в условиях тестирования.
Ошибки на экзаменах по математике
Раздел 1
Вычислительные ошибки
Действия с обыкновенными и десятичными дробями
|
|
|
1. Грубые Оошибки допускаются при выполнении действий с обыкновенными дробями:
а) 
, правильное решение: 
б) 
, правильное решение: 
в) 
правильное решение:
.
2. При выполнении совместных действий с десятичными и обыкновенными дробями довольно часто обыкновенные дроби заменяются их десятичными приближениями, тогда результат выполнения всех действий оказывается приближенным, а не точным.
Например, 
. 0,6- приближенное значение суммы.
. 
- точное значение суммы.
3. При упрощении выражений, содержащих бесконечные периодические дроби, следует эту бесконечную десятичную дробь не округлять, а записать в виде обыкновенной дроби, так как результат округления есть приближенное значение бесконечной периодической дроби.
Например:
а), 0,(6) =0,66666…= 
1, 24(65)=
б) =1,24+0,0065+ 0,000065+0,00000065+…=1 
=
=1 
4. При выполнении действий с десятичными дробями:
а) 2,6 2,60
1,17 - неправильно; правильно будет: 1,17
1,57 1,43
б) 1,9 ∙ 0,01 ≠ 0,19; правильно будет: 1,9∙ 0,01 = 0,019;
в) 7,6: 0,02 ≠ 38; правильно будет: 7,6: 0,02=380.
Для справки
Правила действий с обыкновенными дробями.
обыкновенная дробь, a, b – натуральные числа.
а – числитель дроби, b – её знаменатель;
если а<b, то дробь называется правильной: 
- правильные дроби.
если а≥b, то дробь называется неправильной: 
- неправильные
дроби.
смешанным числом называется число, состоящее из целой и
дробной частей:
- смешанные числа
1. а) Чтобы смешанное число записать в виде неправильной дроби,
надо:
1. целую часть умножить на знаменатель, к полученному произведению прибавить числитель;
2. результат записать в числителе новой дроби;
3. в знаменателе новой дроби записать прежний знаменатель.
Примеры:
, 
.
b) Чтобы выделить целую часть из неправильной дроби, надо:
1) разделить числитель на знаменатель: получится частное и
остаток;
2) частное записать в целую часть;
|
|
|
3) остаток записать в числитель новой дроби;
4) в знаменателе новой дроби записать прежний знаменатель.
Примеры:
;
.
2. а) Сокращение дробей – это деление числителя и знаменателя дроби на одно и то же число, не равное нулю, т.е. это деление числителя и знаменателя на их наибольший общий делитель.
Примеры:
(замечаем, что числитель и знаменатель дроби делятся на одно и то же число 4 и делим числитель и знаменатель на это число).
. 
.
b) Приведение дробей к общему знаменателю.
Чтобы привести две дроби к общему знаменателю, надо:
1) разложить знаменатель каждой дроби на простые множители;
2) умножить числитель и знаменатель первой дроби на недостающие
множители из разложения второго знаменателя;
3) умножить числитель и знаменатель второй дроби на недостающие множители из первого разложения.
Примеры: приведите дроби к общему знаменателю 
.
Разложим знаменатели на простые множители: 18=3∙3∙2, 15=3∙5
умножили числитель и знаменатель дроби на недостающий множитель 5 из второго разложения.
числитель и знаменатель дроби на недостающие множители 3 и 2 из первого разложения.
= 
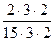, 90 – общий знаменатель дробей .
3. а) Сложение и вычитание дробей с разными знаменателями:.
Ччтобы сложить (вычесть) дроби с разными знаменателями, надо:
1. записать их с общим знаменателем;
2. сложить (вычесть) числители получившихся дробей, результат записать в числитель новой дроби;
3. в знаменатель новой дроби записать общий знаменатель.
Примеры:
b) Умножение дробей.
Чтобы умножить дроби, надо:
1. перемножить их числители и результат записать в числитель новой дроби;
2. перемножить знаменатели и результат записать в знаменатель новой дроби;
3. сократить (если можно) полученную дробь.
Примеры:
Деление дробей.
Чтобы разделить одну дробь на другую, надо:
1. Делимое (первую дробь) оставить без изменения;
2. делитель (вторую дробь) заменить на обратную ей (поменять числитель и знаменатель местами);
3. выполнить умножение первой дроби на вторую по правилу 5.
Примеры:
.
|
|
|
