 |
Два неравенства называются равносильными, если множества их решений совпадают
|
|
|
|
Решение линейных неравенств вида ax>b, ax<b, ax≥b,ax≥b,b<ax<c.
ax>b (1)
Если a>0, то неравенство (1) равносильно неравенству x> b/a, x  (b/a;+∞).
(b/a;+∞).
Если a<0, то неравенство (1) равносильно неравенству x<b/a, x  (-∞; b/a).
(-∞; b/a).
Eсли a=0, то 0x>b, если b<0, то x  (-∞; +∞),
(-∞; +∞),
если b>0, то решений нет,
если b = 0, то решений нет.
ax<b (2)
Если a>0, то неравенство (1) равносильно неравенству x<b/a, x  (-∞; b/a). Если a<0, то неравенство (1) равносильно неравенству x> b/a, x
(-∞; b/a). Если a<0, то неравенство (1) равносильно неравенству x> b/a, x  (b/a;+∞).
(b/a;+∞).
Eсли a=0, то 0x<b, если b<0, то решений нет,
если b>0, x  (-∞; +∞),
(-∞; +∞),
если b = 0, то решений нет.
ax≤b (3)
Если a>0, то неравенство (1) равносильно неравенству x< b/a, x  (-∞; b/a]. Если a<0, то неравенство (1) равносильно неравенству x > b/a, x
(-∞; b/a]. Если a<0, то неравенство (1) равносильно неравенству x > b/a, x  [b/a;+∞).
[b/a;+∞).
Eсли a=0, то 0x≤b, если b<0, то решений нет,
если b>0, x  (-∞; +∞),
(-∞; +∞),
если b = 0, x  (-∞; +∞).
(-∞; +∞).
ax≥b(4)
Если a>0, то неравенство (1) равносильно неравенству x > b/a, x  [b/a;+∞). Если a<0, то неравенство (1) равносильно неравенству x< b/a, x
[b/a;+∞). Если a<0, то неравенство (1) равносильно неравенству x< b/a, x  (-∞; b/a].
(-∞; b/a].
Eсли a=0, то 0x≥b, если b>0, то решений нет,
если b<0, x  (-∞; +∞),
(-∞; +∞),
если b = 0, x  (-∞; +∞).
(-∞; +∞).
b<ax<c (5)
Если a>0, то неравенство (1) равносильно неравенству b/a<x<c/a, x  (b/a;c/a). Если a<0, то неравенство (1) равносильно неравенству c/a<x< b/a, x
(b/a;c/a). Если a<0, то неравенство (1) равносильно неравенству c/a<x< b/a, x  (c/a; b/a).
(c/a; b/a).
Если a=0, то b<0x<c, если b<0, c>0, то x  (-∞; +∞),
(-∞; +∞),
если b>0, c>0 или b<0, c<0 или b>0, c<0, то решений
нет.
30. Решите неравенство:  .
.
Упражнение 4
Решите неравенство (x-9)2(x+6)(x+5)2 ≤ 0.
Ответ: (-∞; -3)U(1;+∞) – неверный.
Правильный ответ (-∞; -3)U(1; 5) U (5;+∞). Ошибка заключается в том, что при решении этого неравенства методом интервалов не исключено число 5, при этом значении x неравенство обращается в равенство.
| Задание 5 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите
неравенство
 . .
| (-∞; -3) U(1;+∞) | Число 5 из интервала (1;+∞) не является решением. | (-∞; -3)U (1; 5) U (5;+∞). | При решении этого неравенства методом интервалов из множества решений не исключено число 5, при этом значении x неравенство обращается в равенство. |
| Решение |  1.Нули числителя x=5.
2. Нули знаменателя
x=1, x=-3.
3.Отмечаем найденные точки на оси.
4.Определяем знак функции, стоящей в левой части неравенства в каждом из полученных интервалов.
1.Нули числителя x=5.
2. Нули знаменателя
x=1, x=-3.
3.Отмечаем найденные точки на оси.
4.Определяем знак функции, стоящей в левой части неравенства в каждом из полученных интервалов.
 5. Записываем ответ в соответствии со знаком неравенства:
(-∞; -3)U(1; 5) U (5;+∞).
5. Записываем ответ в соответствии со знаком неравенства:
(-∞; -3)U(1; 5) U (5;+∞).
|
|
|
|
Упражнение 5
Решите неравенство: 
| Задание 6 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Укажите наименьшее натуральное число, которое удовлетворяет неравенству: │1-x│>2 | В определении границ интервала | Ошибка в том, что число 3 не принадлежит интервалу (3; +∞), наименьшее натуральное число, принадлежащее этому интервалу это 4. | ||
| Решение | │1-x│>2  │1-x│2>22 │1-x│2>22  (1-x-2)(1-x+2) > 0 (1-x-2)(1-x+2) > 0
  (-1-x)(3-x) > 0 (-1-x)(3-x) > 0  x x  (-∞; -1) U(3; +∞), наименьшее натуральное число, которое принадлежит интервалу
(3; +∞)- это число 4. (-∞; -1) U(3; +∞), наименьшее натуральное число, которое принадлежит интервалу
(3; +∞)- это число 4.
| |||
| Для справки | Интервал (a; +∞) - это множество действительных чисел, строго больших a. |
Упражнение 6
Укажите наименьшее натуральное число, которое удовлетворяет неравенству: │x + 5│>2.
Для справки
Чтобы решить неравенство методом интервалов (например,
х² + х > 6), надо:
1) перенести все слагаемые в левую часть так, чтобы правая часть оказалась равной нулю (получим: х² + х – 6 > 0);
2) найти область определения функции, стоящей в левой части (для данной функции y= х² + х – 6 х – любое число);
3) приравнять левую часть к нулю и решить полученное уравнение (х² + х – 6 = 0, D = 25, x1=2, x2= -3);
4) отметить на числовой прямой область определения и полученные решения уравнения, в результате прямая разобьётся на некоторое число промежутков (на 3):
|
|
|
 |


-3 2
5) в каждом из получившихся промежутков выбрать по точке
(возьмём в первом промежутке -4, во втором 0, в третьем 3);
6) вычислить значение функции, стоящей в левой части неравенства пункта 1 (х² + х – 6 > 0), в каждой из выбранных точек (в точке х=-4 х² + х – 6=6, в точке х=0 х² + х – 6 =-6, в точке х=3 х² + х – 6=6);
7) над каждым из промежутков на числовой прямой поставить знак ‘+’, если вычисленное значение в соответствующей точке положительно, и знак ‘-’ - если отрицательно (в первом и третьем промежутке получились положительные значения, во втором – отрицательное):


 + - +
+ - +
-3 2
в ответе записать промежутки, знак которых совпадает со знаком неравенства
(-∞; -3) или (2; +∞)).
31.Решите неравенство:  . Ответ: [2;+∞) – неверный правильный ответ: [2;+∞) и x =1. Ошибка заключается в том, что при решени этого неравенства методом интервалов пропущена точка х =1, в которой значение функции, стоящей в левой части неравенства равно нулю, при этом знак второго множителя не имеет значения.
. Ответ: [2;+∞) – неверный правильный ответ: [2;+∞) и x =1. Ошибка заключается в том, что при решени этого неравенства методом интервалов пропущена точка х =1, в которой значение функции, стоящей в левой части неравенства равно нулю, при этом знак второго множителя не имеет значения.
| Задание 7 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите
неравенство
 . .
| [2;+∞) | Потеряно решение х =1 | [2;+∞) и x =1. | Ошибка заключается в том, что при решени этого неравенства методом интервалов пропущена точка х =1, в которой значение функции, стоящей в левой части неравенства равно нулю, при этом знак второго множителя не имеет значения |
| Решение |  .
1.Найдем область определения функции, стоящей в левой части неравенства: подкоренное выражение должно быть неотрицательным x2-3x+2≥0,
решение этого неравенства (- ∞; 1] .
1.Найдем область определения функции, стоящей в левой части неравенства: подкоренное выражение должно быть неотрицательным x2-3x+2≥0,
решение этого неравенства (- ∞; 1]  [ 2;+∞),
2.Найдем нули функци x=1, x=2(x=1,5 не входит в указанную область определения).
Определяем знаки функции y = [ 2;+∞),
2.Найдем нули функци x=1, x=2(x=1,5 не входит в указанную область определения).
Определяем знаки функции y =  на каждом из промежутков (- ∞; 1] и [2;+∞). В ответе запишем значения x, при которых значения функции y =
на каждом из промежутков (- ∞; 1] и [2;+∞). В ответе запишем значения x, при которых значения функции y =  неотрицательны, т.е. [2;+∞) и x =1. неотрицательны, т.е. [2;+∞) и x =1.
|
Упражнение 7
Решите неравенство: 
| Задание 8 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите неравенство 0,2x-3 >1. | (3; +∞) | Не изменен знак неравенства | (-∞;3). | Ошибка в том, что показательная функция y = 0,2x – убывающая, поэтому при переходе от значений функции к значениям аргумента знак неравенства изменяется |
| Решение | 0,2x-3 >1  x-3 < 0 x-3 < 0  x <3 x <3  x x  (-∞;3). (-∞;3).
| |||
| Для справки |
Если a >1, то неравенство af(x)> ag(x) равносильно неравенству
f(x) > g(x), (неравенство af(x)< ag(x) равносильно неравенству f(x)< g(x))
Если 0< a<1, то неравенство af(x)> ag(x) равносильно неравенству
f(x) < g(x), (неравенство af(x)< ag(x) равносильно неравенству f(x)> g(x)) |
|
|
|
Упражнение 8
Решите неравенство 0,1x-4 ≤ 1.
| Задание 9 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите неравенство 0,1x >0,01. | (2; +∞) | Не изменен знак неравенства | (-∞;2) | Ошибка в том, что при решении неравенства неверно использовалось свойство монотонности функции y = 0,1x. Показательная функция y = 0,1x – убывающая, поэтому, если 0,1x >0,12, то x<2. |
| Решение | 0,1x >0,01, так как показательная функция y = 0,1x – убывающая, то x<2, то x  (- ∞; 2) (- ∞; 2)
|
Упражнение 9
Решите неравенство 0,5x <0,25.
| Задание 10 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите неравенство (⅓)2x-8∙(⅓) x -9>0 | (-2; +∞) | Не решено неравенство (1/3)x >9 | (-∞;-2) | Неравенство y2 -8y – 9>0. не решено относительно y. |
| Решение | (⅓)2x -8∙(⅓) x -9>0, пусть (1/3)x =y, тогда данное неравенство будет иметь вид:
y2 -8y – 9>0,
решим это неравенство методом итервалов, получим y>9 или y <-1.
Возвращаясь к замене, получим (1/3)x >9 или(1/3)x <-1.
Решение первого неравенства: x < -2, x  (-∞;-2) (основание показательной функции 1/3 <1), второе неравенство решений не имеет.
Ответ: (-∞;-2). (-∞;-2) (основание показательной функции 1/3 <1), второе неравенство решений не имеет.
Ответ: (-∞;-2).
|
Упражнение 10
Решите неравенство: 0,04x + 0,2x - 2 ≤ 0.
32. Решите неравенство: log2x < 3. Ответ: (-∞;8) – неверный. Правильный
ответ: (0;8). Ошибка в том, что не учтена область определения логарифмической функции y = log2x, D(og2x) = (0; +∞), решение данного неравенства – пересечение промежутков (-∞;8) и (0; +∞).
| Задание 11 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите неравенство log2x < 3 | (-∞;8) | Не учтена область определения логарифмической функции | (0;8) | Не учтена область определения логарифмической функции y = log2x, D(log2x) = (0; +∞), решение данного неравенства – пересечение промежутков (-∞;8) и (0; +∞). |
| Решение | log2x < 3  
|
|
|
|
Упражнение 11
log0,5x > -1
33. Решите неравенство log0,5x >3. Ответ: (1/8; + ∞) – неверный.
Правильный ответ: (0;1/8).
Ошибка в том, что логарифмическая функции y = log0,5x – убывающая, поэтому при переходе от значений функции к значениям аргумента знак неравенства изменяется.
| Задание 12 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите неравенство log 0,5x >3 | (1/8; + ∞) | Не изменен знак неравенства | (0;1/8) | Логарифмическая функции y = log0,5x – убывающая, поэтому при переходе от значений функции к значениям аргумента знак неравенства изменяется. |
| Решение | log 0,5x >3  
| |||
| Для справки | Неравенство loga f(x)> loga g(x) равносильно неравенству f(x)> g(x), при a>1 и дополнительных условиях g(x)>0, f(x)>0. Неравенство loga f(x)> loga g(x) равносильно неравенству f(x)< g(x),при 0<a<1 и дополнительных условиях g(x)>0, f(x)>0. |
Для справки
Неравенство loga f(x)> loga g(x) равносильно неравенству f(x)> g(x),при
a>1 и дополнительных условиях g(x)>0, f(x)>0.
Неравенство loga f(x)> loga g(x) равносильно неравенству f(x)< g(x),при
0<a<1 и дополнительных условиях g(x)>0, f(x)>0.
Упражнение 12
log0,1x ≤2.
34.Решите неравенство 0,2x-3 >1. Ответ: (3; +∞) – неверный. Правильный ответ (-∞;3). Ошибка в том, что показательная функция y = 0,2x – убывающая, поэтому при переходе от значений функции к значениям аргумента знак неравенства изменяется.
Для справки
Если a >1, то неравенство af(x)> ag(x) равносильно неравенству
f(x) > g(x), (неравенство af(x)< ag(x) равносильно неравенству f(x)< g(x))
Если 0< a<1, то неравенство af(x)> ag(x) равносильно неравенству
f(x) < g(x), (неравенство af(x)< ag(x) равносильно неравенству f(x)> g(x))
35. Решите уравнение lgx + lg(x - 3) > 1. Решение x + x -3 > 10, x > 6,5 и ответ (6,5;+ ∞) - неверны. Ошибка в том, что сумма логарифмов равна не логарифму суммы, а логарифму произведения, поэтому нужно сравнивать не сумму а произведение аргументов с числом 10, т.е. x (x -3) > 10 с учетом области определения получим правильный ответ: (5;+ ∞).
| Задание13 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите неравенство lgx + lg(x - 3) > 1 | (6,5;+ ∞) | Неверно применяются свойст ва логарифмов | (5;+ ∞). | Сумма логарифмов равна не логарифму суммы, а равна логарифму произведения, поэтому нужно сравнивать не сумму, а произведение аргументов с числом 10. |
| Решение | lgx + lg(x - 3) >1     x x  (5;+ ∞). (5;+ ∞).
|
Упражнение 13
Решите неравенство lg(x - 4) + lg(x +4) < 1
| Задание 14 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите неравенство sin x >0,5. | x> 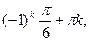

| неверно определен промежуток изменения для x | 
 ), ),

| Решение тригонометрических неравенств не аналогично решению линейных неравенств (3х =6, х=2. 3х >6, x > 2). |
| Решение | Так как период функции y = sinx равен 2π, то рассмотрим решение неравенства
sin x > 0,5 на этом периоде, например, на отрезке [0;2π].
1.Отметим ординату, равную 0,5.
2.На единичной окружности отметим две точки, ординаты которых равны 0,5.  3.Запишем угол, соответствующий одной из этих точек из отрезка [0;2π], это угол
3.Запишем угол, соответствующий одной из этих точек из отрезка [0;2π], это угол  .
4.Двигаясь от этой точки по окружности вверх (проходим через точку .
4.Двигаясь от этой точки по окружности вверх (проходим через точку  ), называем угол, соответствующий второй точке.
5. Второй угол будет ), называем угол, соответствующий второй точке.
5. Второй угол будет  .
6.x .
6.x 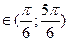 , с учетом периодичности функции y = sinx получим ответ: , с учетом периодичности функции y = sinx получим ответ:   . .
| |||
| Для справки | Алгоритм решения неравенства sinx >a (sinx <a),│a│<1 с помощью единичной окружности: 1.Отметить ординату, равную a. 2. Найти на окружности две точки, у которых такая ордината. 3.Записать угол, соответствующий одной из таких точек. 4. Определить в соответствии со знаком неравенства по какой из двух дуг окружности нужно двигаться к другой отмеченной точке. 5. Называя промежуточные углы, определить угол, соответствующий второй отмеченной точке. 6. Записать ответ от меньшего угла к большему, добавляя период. |
|
|
|
Упражнение 14
Решите неравенство: cosx <  .
.
6.
| Задание 15 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите неравенство cosx < 0,5. | 
| неверно определен промежуток изменения для x |  
| Ошибка в выборе интервала между двумя значениями аргумента, в которых значение функции равно 0,5. |
| Решение | Так как период функции y = cosx равен 2π, то рассмотрим решение неравенства cosx < 0,5 на этом периоде., например, на [0;2π].
1. Отметим абсциссу 0,5.
2. На единичной окружности отметим две точки, у которых такие абсциссы.
3. Запишем угол, соответствующий одной из этих точек из отрезка [0;2π], это угол  .
4. Двигаясь по окружности вверх через точки .
4. Двигаясь по окружности вверх через точки  , назовем угол, соответствующий второй точке.
5. Это угол , назовем угол, соответствующий второй точке.
5. Это угол 
 6. x
6. x  , с учетом периодичности функции y = cosx получим ответ: , с учетом периодичности функции y = cosx получим ответ:  
| |||
| Для справки | Алгоритм решения неравенства cosx >a (cosx <a),│a│<1 с помощью единичной окружности: 1.Отметить абсциссу, равную a. 2. Найти на окружности две точки, у которых такая абсцисса. 3.Записать угол, соответствующий одной из таких точек. 4. Определить в соответствии со знаком неравенства по какой из двух дуг окружности нужно двигаться к другой отмеченной точке. 5. Называя промежуточные углы, определить угол, соответствующий второй отмеченной точке. 6. Записать ответ от меньшего угла к большему, добавляя период. |
Упражнение 15
Решите неравенство sinx <- 0,5.
| Задание16 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите неравенство tg x ≥ 1 | 
| Число 2πk, k  не принадлежит множеству решений неравенства не принадлежит множеству решений неравенства
| 
| Ошибка в том, что при решении неравенства не учтена область определения функции у = tg x. |
| Решение | Так как функция y = tg x периодическая с периодом π и определена для всех x  R/ R/  , то рассмотрим решение неравенства на периоде, например, на интервале (-π/2;π/2). На этом интервале функция y= tg x возрастает, а значение,равное 1 принимает при x = π/4, следовательно, решение на этом периоде есть интервал [ π/4; π/2).
C учетом периода, решение данного неравенства – это серии промежутков вида: , то рассмотрим решение неравенства на периоде, например, на интервале (-π/2;π/2). На этом интервале функция y= tg x возрастает, а значение,равное 1 принимает при x = π/4, следовательно, решение на этом периоде есть интервал [ π/4; π/2).
C учетом периода, решение данного неравенства – это серии промежутков вида:  . .
|
Упражненеие 16
Решите неравенство tg x ≤ 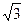
| Задание 17 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите
неравенство
 . .
| [0; 1) | Пропущены решения: (-∞;0). | (-∞;1). | При решении рассмотрен лишь случай, когда правая часть неравенства неотрицательна. |
| Решение |     x x  (-∞; 1) (-∞; 1)
| |||
| Для справки | Неравенство вида  равносильно следующей совокупности неравенств: равносильно следующей совокупности неравенств: 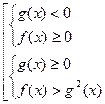
|
Упражнение 17
Решите неравенство:  .
.
| Задание18 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите неравенство (x-5)· log2 (x/2)<0. | (-∞;2) U (2;5). | Интервал (-∞;2) не является решением данного неравенства. | (2;5) | Не учтена область определения функции y=(x-5)log2 (x/2) |
| Решение | (x-5)log2 (x/2)< 0. Решим неравенство методом интервалов. 1. D((x-5)log2 (x/2)) =(0; + ∞). 2. Нули функции y = (x-5)log2 (x/2): x=5, x=2. 3.Отмечаем на оси D((x-5)log2 (x/2)) и нули функции. 4. Определяем знак в каждом из промежутков (0;2), (2;5), (5; + ∞). 5. Выбираем промежуток в соответствии со знаком данного неравенства: (2;5) | |||
| Для справки | Чтобы решить неравенство методом интервалов надо: 1.Привести неравенство к виду f(x) = 0 2.Найти область определения функции y=f(x) 3.Найдите нули функци y=f(x) 4.Отметить на оси OX нули функции и область ее определения 5.Определить знак функции f(x) в каждом из промежутков, на которые нули функции и область ее определения разбивают ось. 6. Записать ответ в соответствии со знаком неравенства. |
Упражнение 18
Решите неравенство: (x+1)log0,5 (x-4) < 0.
| Задание 19 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите неравенство:

| 
| x = πn,

|  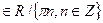
| При решени не учтена область определения дроби. |
| Решение |  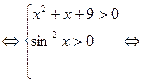  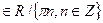
| |||
| Для справки | Дробь 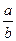 определена при условии: b ≠ 0. определена при условии: b ≠ 0.
|
Упражнение 19
Решите неравенство: 
| Задание 20 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите неравенство:

| 
| Не при всех x  определены подкоренные выражения определены подкоренные выражения
| [1;3] | При решении не учтена область определения арифметического корня. |
| Решение | Поскольку по определению арифметического квадратного корня каждый из корней суммы  неотрицателен, то эта сумма положительна (каждый корень обращается в ноль при разных значениях x) для всех x, удовлетворяющих системе: неотрицателен, то эта сумма положительна (каждый корень обращается в ноль при разных значениях x) для всех x, удовлетворяющих системе:  .
Решение этой системы и будет решением данного неравенства. .
Решение этой системы и будет решением данного неравенства.
| |||
| Для справки | Арифметическим квадратным корнем из числа a называется неотрицательное число, квадрат которого равен a. Область определения функции
y =  есть множество неотрицательных чисел, т.е. есть множество неотрицательных чисел, т.е.
 . .
|
Упражнение 20
Решите неравенство 
| Задание 21 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите неравенство 
| x 
| При x=1 левая часть неравенства равна нулю | x 
| Числитель дроби, стоящей в левой части неравенства больше нуля или равен ему при x=1, это значение не было исключено из решения |
| Решение | Знаменатель дроби  трехчлен с положительным первым коэфффициентом и отрицательным дискриминантом, значит при всех x он принимает положительные значения. Числитель этой дроби, больше нуля при всех x, кроме 1. Значит решения данного неравенства: x трехчлен с положительным первым коэфффициентом и отрицательным дискриминантом, значит при всех x он принимает положительные значения. Числитель этой дроби, больше нуля при всех x, кроме 1. Значит решения данного неравенства: x 
| |||
| Для справки | │x│≥ 0, равенство выполняется, если x = 0. |
Упражнение 21
Решите неравенство 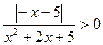
| Задание 22 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите неравенство: lg sinx + lg cosx < 0 | x 
| Не при всех x определены логарифмы в левой части неравенства | (2πn;π/2+2πn), n 
| Не найдена область определения левой части неравенства |
| Решение | Найдем область определения функции, стоящей в левой части
данного неравенства: 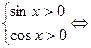 x x   .При этих значениях x sin x и cosx больше нуля и меньше 1, а поскольку основание логарифма 10>1, то по свойству логарифмической функции с таким основанием каждый из логарифмов отрицателен, следовательно, решения неравенства - это все x из найденной области определения, т.е. .При этих значениях x sin x и cosx больше нуля и меньше 1, а поскольку основание логарифма 10>1, то по свойству логарифмической функции с таким основанием каждый из логарифмов отрицателен, следовательно, решения неравенства - это все x из найденной области определения, т.е.  . .
| |||
| Для справки | Знаки логарифмической функции y = logax с основанием a >1: если x >1, то logax >0; если 0 < x <1, то logax < 0. |
Упражнение 22
Решите неравенство lоg 0,5sinx + lоg0,5cosx > 0
| Задание23 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите неравенство:

| x 
| При x=1 левая часть неравенства равна нулю | x 
| Не учтено, что неравенство не- строгое |
| Решение |    │x-1│>0 │x-1│>0  x x 
|
Упражнение 23
Решите неравенство:

| Задание 24 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите неравенство logx+2(5- -│x-3│) ≥ 0 | (-2;7] | x =-1- не решение данного неравенства | (-2;-1)U(-1;7]. | Ошибка в том, что при решении неравенства не учтено, что x = -1 не входит в область определения функции y = logx+2(5-│x-3│. |
| Решение | logx+2(5-│x-3│)≥ 0  
 
| |||
| Для справки | Неравенство loga b > 0 равносильно нервенству (a-1)(b-1) > 0 при условии b>0, a>0, a ≠ 1. |
Упражнение 24
Решите неравенство: logx +3(5x-3)≥ 0
| Задание25 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите неравенство:

| [-2- 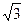 ;-1] ;-1] 
| отрезок [-2- 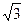 ;
-1] – не решения данного неравенства ;
-1] – не решения данного неравенства
| 
| Не учтено необходимое условие, при котором данное неравенство имеет решение: 1+2x ≥ 0 |
| Решение |
  
 
    
|
Упражнение 25
Решите неравенство: │x2 -7│< -x -5.
| Задание26 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите неравенство:
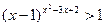
| (1;2)U(2; +∞). | Ошибка в том, что не все решения найдены. | (1;2)U(2; +∞) U { -1, -2, -3…}. | Решения (1;2)U(2; +∞) найдены при условии, что x-1>0, x ≠1. По определению степени с целым показателем основание этой степени может быть и отрицательным, и равным 1. |
| Решение |    
|
Упражнение 26
Решите неравенство  .
.
| Задание27 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите неравенство: sin(πcosx) > 0. | Решений нет. | При некоторых x неравенство верно. |  , , 
| Причина ошибки в том, что решение неравенства
2πk < π cosx < π +2πk (1), k  - это объединение решений этого неравенства для каждого k - это объединение решений этого неравенства для каждого k  ,а не общие решения для всех k ,а не общие решения для всех k  . Для k = 0 неравенство (1) имеет решения. . Для k = 0 неравенство (1) имеет решения.
|
| Решение | Так как функция y = cosx периодическая с периодом 2π, то
рассмотрим решение на периоде, например, на отрезке [-π;π]. Положительные значения функция y = sin (πcosx) принимает, если
2πk < π cosx < π +2πk, k  или 2k < cosx < 1+2k, k или 2k < cosx < 1+2k, k  .
При k = 0, 0 < cosx < 1, на [-π;π] косинус принимает положительные значения для .
При k = 0, 0 < cosx < 1, на [-π;π] косинус принимает положительные значения для  или с учетом периода или с учетом периода  , ,  При остальных целых │k│≥1 неравенство k < cosx < 1 +2k, решений не имеет.
При остальных целых │k│≥1 неравенство k < cosx < 1 +2k, решений не имеет.
|
Упражнение 27
Решите неравенство: cos(πcosx) > 0.
| Задание28 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите неравенство:
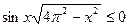
|  . .
| Потеряно решение x =-2π. | 
| Решения данного неравенства - не только значения x из отрезков, в которых sinx ≤ 0, но и отдельные значения x, при которых sinx = 0, a 4π2 – x2 ≥ 0. |
| Решение | 1. Найдем область определения функции 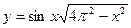 :
4π2 – x2 ≥ 0 :
4π2 – x2 ≥ 0 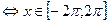 2.Найдем нули функции
2.Найдем нули функции 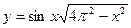 : sinx = 0 или
4π2 – x2 =0 для : sinx = 0 или
4π2 – x2 =0 для  , x =-2π; -π, 0, π; 2π.
3. Отметим область определения и нули функции на оси ox.
4. В каждом из интервалов определим знаки функции , x =-2π; -π, 0, π; 2π.
3. Отметим область определения и нули функции на оси ox.
4. В каждом из интервалов определим знаки функции 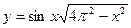 5.Запишем ответ в соответствии со знаком неравенства:
5.Запишем ответ в соответствии со знаком неравенства: 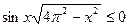 : : 
|
Упражнение 28
Решите неравенство: - 
| Задание29 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите неравенство: │1+log2 x│sin2πx ≤1 |

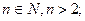 [0,25;0,5]
[0,25;0,5]
| Потеряно решение x = 1 |

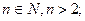 [0,25;0,5],
x=1.
[0,25;0,5],
x=1.
| Решения 
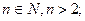 [0,25;0,5] найдены при условии, что основание > 0, │1+log2x│≠1. По определению степени с целым показателем основание этой степени может быть и нулем, и равным 1.
[0,25;0,5] найдены при условии, что основание > 0, │1+log2x│≠1. По определению степени с целым показателем основание этой степени может быть и нулем, и равным 1.
|
| Решение |
│1+log2 x│sin2πx ≤1
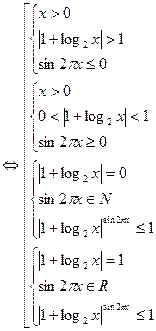  
|
Упражнение 29
Решите неравенство:
│1+ lg x│сos0,5πx ≥ 1.
Ответы к упражнениям
1. а)Ответ (-∞; -4] неправильный.
Ошибка в том, что при делении обеих частей неравенства на отрицательное число -2,5 знак неравенства не был изменен.
Правильный ответ: [-4;+∞).
б).Ответ: (4;+∞) – неправильный.
Для решения этого неравенства надо обе его части разделить на -1 и при этом изменить знак неравенства (≥ на ≤).
|
|
|


