Далее приводятся примеры задач с несколькими решениями. Решения с номером 1 встречаются во многих учебных пособиях, приводятся абитуриентами на экзаменах. Решения с номером 2 или 3 – рациональные.

 

6. Решите уравнение:

 

Решение1

 

Найдем нули многочленов, стоящих под знаком модуля:

 

x- 3 = 0, x =3. 2x + 1= 0, x = -0,5.

 

Эти точки разбивают ось OX на три промежутка. Решим данное уравнение

на каждом из промежутков.

 

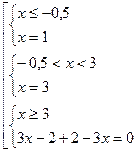
x .

Ответ: x

 

 

Решение 2

 

.

Ответ: x

 

Для справки:

Свойство модулей: │a│+ │b│≥ a + b, равенство достигается при условии

a ≥ 0, b ≥ 0.

 

7. Решите уравнение: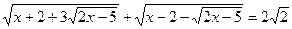

 

Решение 1

Сделаем замену: тогда

Выразим переменную x через y. x = (y² +5)/2. Подставим в исходное уравнение:

Приведя подобные слагаемые и умножив обе части уравнения на , получим равносильное уравнение

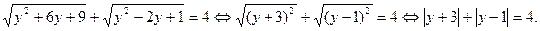
Воспользуемся тем, что y ≥0. Тогда уравнение примет вид По определению модуля 0 ≤ y ≤ 1. Вернемся к подстановке: тогда . Ответ: [2,5;3].

 

Решение 2

 

Выделим под знаком корней квадраты двучленов, предварительно

умножим и разделим подкоренные выражения на 2:

 

, далее , ,

, откуда .

, по свойству модуля числа будем иметь: , решение этого неравенства:

 

8. Решите уравнение:

 

(1)

 

 

Решение 1

 

Все корни исходного уравнения содержатся среди корней совокупности уравнений:

 

, которые запишем в виде

 

.

Корни полученной совокупности уравнений содержаться среди корней совокупности уравнений:

 

Решая полученные уравнения, найдем: x₁ =3, x₂ = , x₃ = ,

x₄ = . Подстановкой в исходное уравнение убеждаемся, что подходит только x₁ =3.

 

Ответ: 3

 

 

Решение 2

 

Уравнение (1) имеет решение, если его правая часть неотрицательна, т.е. 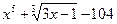≥ 0. Поскольку функция y = возрастающая, то

она принимает положительные значения при x, не меньших двух (при x =2 y= ), и - навярняка при x ≥3 (при x = 3, , т.е. решения уравнения (1) необходимо удовлетворяют условию x > 2.

При этих x = , и уравнение (1) сводится к решению уравнения (2) при x > 2.

Корни уравнения (2) содержатся среди решений совокупности двух уравнений:

 

(3)

Первое уравнение совокупности имеет решение x = 3, а второе - x = .

Очевидно, что x = 3 – корень уравнения (2), а следовательно, и (1). Второй корень следует проверить.

Проверка: = ,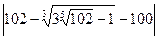

= , полученные числовые равенства неверны, так как при x =3, а <3, т.е. <0; значит, число - не корень данного уравнения.

 

Ответ: x =3

 

 

9. Найдите сумму корней уравнения sinx + cosx = 1, принадлежащих промежутку [0;π].

 

Решение 1

Умножим обе части урвнения на , получим sinx + cosx = .

Заменим на sinπ/4 и cos π/4: cos π/4sinx + sin π/4cosx = или по формуле синуса суммы sin(x+ π/4) = . Далее по формуле для решения простейшего тригонометрического уравнения будем иметь:

x+ π/4 = (-1)^k π/4 +πk, k 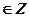, x = - π/4 + (-1)^k π/4 +πk, k 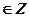. Найдем, какие из

корней этой серии принадлежат отрезку [0;π].

 

При k=0:

x = - π/4 + (-1)⁰ π/4, x = 0;

при k=1: x = - π/4 + (-1)¹ π/4 + π = π/2;

при k=2: x = - π/4 + (-1)² π/4 + 2π = 2 π.

Корни 0 и π/2 принадлежатотрезку [0;π]. Их сумма равна π/2.

Ответ: π/2.

 

Решение 2

Используем свойства функций y =sinx и y = cosx на [0;π].

Так как множество значений этих функций отрезок [-1;1], а для х из (π/2; π] значения cosx отрицательны, то на этом интервале уравнение sinx + cosx = 1

не имеет решений. В интервале (0; π/2) решений нет, поскольку значения синуса и косинуса на этом интервале численно равны катетам прямоугольного треугольника, гипотенуза которого равна 1. Остается проверить x=0 и x= π/2. Эти значения являются решениями данного уравнения на отрезке [0;π]. Их сумма равна π/2.

 

Ответ: π/2.

 

10. Решите уравнение:

 

(1)

 

Решение 1

Возведя обе части уравнения в квадрат, получим равносильное уравнение

(2). После возведения этого уравнения в квадрат, перейдем к уравнению (3), являющемуся следствием уравнения (2). Сделав замену переменной

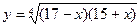получим уравнение u² - 32u +112 =0.

Решения этого уравнения u₁= 4, u₂= 28.

Следовательно, приходим к совокупности двух уравнений ,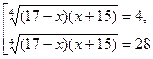

которая является следствием уравнения (3).

Первое уравнение совокупности имеет единственное решение x=1.

А второе – решений не имеет. Подставив в исходное уравнение x=1, убеждаемся что он является корнем исходного уравнения.

Ответ: 1.

Решение 2

Заметим, что сумма подкоренных выражений равна 32, поэтому целесообразна такая замена:

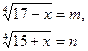тогда а m + n = 4 и данное уравнение равносильно системе

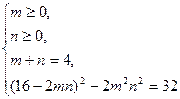
Последнее уравнение имеет решения mn = 28 или mn = 4, учетом с

уравнения m + n = 4. Получаем, m =n =2.

откуда x=1.

 

 

Решение 3

 

Пременим к левой части уравнения неравенство между средним арифметическим и средним квадратичным двух неотрицательных чисел:

 

. Равенство достигается при условии равенства слагаемых, т.е. 17-x = 15+x, откуда x =1.

 

Для справки:

Неравенство между средним арифметическим и средним квадратичным двух положительных чисел: , a > 0, b>0.

 

11. Найдите, при каких значениях р уравнение 1+ рsinx = р² – sin²x имеет решения.

Решение 1

 

Обозначив sinx через y, получим уравнение 1+ рy= р² –y² или

 

y² + py – p² +1= 0.

 

Тогда, c учетом множеств значений sinx и cosx, задача сведется к следующей:

при каком значении p хотя бы один корень данного уравнения принадлежит промежутку [-1;1]?

 

Это условие выполняется в двух случаях:

 

1. Ровно один корень принадлежит этому промежутку.

2. Оба корня принадлежат этому промежутку.

 

Рассмотрим сначала случаи, когда корень уравнения равен 1 или -1, т.е. 1+ p - p² +1 = 0 или 1- p - p² +1 = 0, откуда p = -2, -1, 1,2.

Теперь условия 1. и 2. будем рассматривать на интервале (-1;1).

Условие 1. выполняется тогда и только тогда, когда значения квадратного трехчлена y² + py – p² +1 на концах интервала (-1;1) разных знаков, т.е.

 

(p²-p-2) (p²+p-2) < 0.

Решая это неравенство, получим

 

Для второго случая должны выполняться следующие условия:

значения квадратного трехчлена в точках x = 1 и x =1 должны быть положительны; дискриминант квадратного трехчлена неотрицателен; абсцисса вершины параболы также принадлежала промежутку(-1;1).

Все эти условия запишем в виде системы:

 

Объединяя все найденные решения, получим ответ:

 

 

Решение 2

 

Обозначив sinx через y, получим уравнение 1+ рy= р² –y² или

 

y² + py – p² +1= 0.

 

Тогда, c учетом множеств значений sinx и cosx, задача сведется к следующей:

при каком значении p хотя бы один корень данного уравнения принадлежит промежутку [-1;1]? Сформулируем и решим противоположную задачу:

при каком значении p ни один корень данного уравнения не принадлежит промежутку [-1;1]?

 

Это условие выполняется тогда и только тогда, когда значение квадратного трехчлена y² + py – p² +1 в точках x =-1 и x = 1 отрицательны, т.е. найдем значения p, удовлетворяющие системе:

 

 

Логическая ошибка допускается, если в качестве значений p,

при которых хотя бы один корень данного уравнения принадлежит промежутку [-1;1], берутся все p, принадлежащие интервалу (-2;2).

Причина в том, что отрицанием условия «ни один корень данного уравнения не принадлежит промежутку [-1;1]» будет объединение двух условий: либо корней нет вообще, либо хотя бы один корень данного уравнения принадлежит промежутку [-1;1].

Поскольку нужен ответ на второй вопрос, то исключим из интервала (-2;2). те значения параметра p, при которых корни уравнения y² + py – p² +1= 0.

не существуют, т.е. D < 0. D = 5p² -4<0 .

Получим ответ

 

12. Решите уравнение (1)

 

Решение 1

 

Проведем цепочку равносильных преобразований

 

 

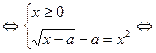
Решая первое уравнение последней системы как квадратное относительно a, получим равносильную систему:

 

 

Решение 2

 

Левую часть данного выражения можно рассматривать как функцию

y = f(f(x)), где f(x) = .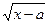

Тогда данное уравнение (1) имеет вид f(f(x)) = x Поскольку функция

f(x) = 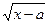монотонно возрастает, то уравнение (1) равносильно уравнению

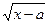= x (2). (cм. справку).

Возведем обе части уравнения (2) в квадрат и решим полученное уравнение x² – x + a = 0 (3) относительно x.

D = 1-4a ≥ 0 при a ≤ 0,25 поэтому уравнение (3) имеет корни

x_1,2 = 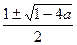при a ≤ 0,25. Уравнение (2) имеет корни уравнения (3), если они удовлетворяют условию x ≥ 0. При a < 0 такой корень только один

x = , при 0≤a < 0,25 корней два, при a = 0,25 корень равен 0,5.

Окончательно получаем ответ: при x = ,

при 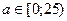x_1,2 = ,

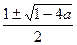при a = 0,25 x =0,5,

при решений нет.

Для справки

Уравнение f(f(x))= x равносильно на области определения функции f(x) уравнению f(x) = x, если функция y = f(x) строго возрастающая на области определения.

 

Доказательство:

Если x_o – корень уравнения f(x) = x, то f(x_o) = x_o – верное числовое равенство. Покажем, что f(f(x_o))= x_o - тоже верное числовое равенство, т.е. x_o – корень уравнения f(f(x))= x.

Так как f(x_o) = x_o верное числовое равенство, а функция y = f(x) строго возрастающая, то верно и равенство f(f(x_o)) = f(x_o). Поскольку f(x_o) = x_o, то f(f(x_o)) = x_o- верное числовое равенство, таким образом, x_o – корень уравнения f(f(x))= x.

Покажем обратное: если x_o- корень уравнения f(f(x))= x, т.е. f(f(x_о))= x_о – верное числовое равенство, то f(x_o) = x_o – тоже верное числовое равенствао, т.е. x_o- корень уравнения f(x) = x.

Предположим, что это не так, т.е. f(x_o) ≠ x_o. Пусть f(x_o) > x_o.

Тогда, так как функция f(x) сторого возрастающая, получим f(f(x_o)) > f(x_o).

По предположению f(x_o) > x_o, тогда по свойству числовых неравенств

f(f(x_o)) > x_o, что противоречит данному условию f(f(x_о))= x_о.

 

Пусть f(x_o) <x_o.

Тогда, так как функция f(x) сторого возрастающая, получим f(f(x_o)) < f(x_o).

По предположению f(x_o) < x_o, тогда по свойству числовых неравенств

f(f(x_o)) < x_o, что противоречит данному условию f(f(x_о))= x_о.

Таким образом, остается только случай равенства f(f(x_о))= x_о.

Итак, каждый корень уравнения f(x) = x является корнем уравнения f(f(x))= x и обратно: каждый корень уравнения f(f(x))= x является корнем уравнения

f(x) = x. Таким образом, уравнения f(f(x))= x и f(x) = x равносильны.

Замечание.

Утверждение, аналогичное приведенному, неверно в случае, если функция

f(x) – убывающая. Например, пусть f(x) = -x убывающая функция на всей област определенеия. Тогда уравнение f(x) = x имеет вид x = -x и имеет единственный корень x = 0. Уравнение f(f(x))= x имеет вид

x = x и имеет бесчисленное множество корней.

 

 

13. Решите уравнение:

(1)

 

Решение 1

Перепишем исходное уравнение в виде: .

 

Возведем в куб левую и правую части уравнения:

x-1 = 1- , которое с учетом О.Д.З. переменной

 

равносильно системе

 

Ответ:1

 

Решение 2

 

Заметим, что число x = 1- корень данного уравнения

Расмотрим функцию f(x) = (2)

 

На всей области определения [0; +∞) функция возрастает и непрерывна.

По теореме о промежуточном значении функции каждое свое значение функция принимает только один раз, значит x=1 – единственный корень данного уравнения.

Ответ:1

 

14. Решите уравнение

 

(1)

 

Решение 1

Перепишем уравнение в виде . Возведя обе части в куб, получим равносильное уравнение

(2)

Воспользовавшись тем,что по условию , получим уравнение (3), которое является следствием уравнения (2).

Возведя обе части уравнения (3) в третью степень, получим:

(x+1)(x+2)(x+3)=-(x+2)³

корни последнего уравнения -2, .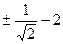

Подстановкой убеждаемся, что корнем является только x = -2.

 

Ответ: x=-2

 

 

Решение 2

 

Заметим, что x = -2 – корень данного уравнения.

 

Расмотрим функцию f(x) = 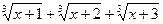(2)

 

На всей области определения (-∞; + ∞) функция возрастает и непрерывна.

По теореме о промежуточном значении функции, каждое свое значение функция принимает только один раз, значит x = -2 – единственный корень данного уравнения.

 

Ответ: x = -2

 

15. Решите уравнение

 

 

Решение 1

Полагаем у= . Тогда

Итак, =2 х=2.

Ответ: x = 2

 

Решение 2

 

Заметим, что x = 2 – корень данного уравнения.
Расмотрим функцию f(x) = (2)

На всей области определения [-2; +∞) функция возрастает и непрерывна.

По теореме о промежуточном значении функции каждое свое значение данная функция принимает только один раз, значит x = 2 – единственный корень данного уравнения.

Ответ: x = 2

 

 

 

16. Решите неравенство:

 

log_x+2 (9x²+15x-6) <2

 

Решение 1

Неравенство равносильно совокупности двух систем:

 

 

Решение 2

 

Данное неравенство равносильно системе:

 

 

Для справки

 

Знак выражения log_a t₁- log_a t₂ совпадает со знаком выражения (a-1)(t₁-t₂) при условии, что a > 0, a ≠ 1, t₁>0, t₂>0. Покажем это:

 

1.Пусть a >1, тогда функция y= log_a t – возрастающая и если t₁>t₂>0, то

log_a t₁- log_a t₂ > 0, а если t₂>t₁>0, то log_a t₁- log_a t₂ < 0. При a >1 a-1> 0 и если t₁>t₂, то (a-1)(t₁-t₂) > 0, а если t₂>t₁, то (a-1)(t₁-t₂) <0, т.е. знак выражения

log_a t₁- log_a t₂ совпадает со знаком выражения (a-1)(t₁-t₂).

 

2. Пусть 0 <a <1, тогда функция y= log_a t - _{_} убывающая и если t₁>t₂>0, то

log_a t₁- log_a t₂ , 0, а если t₂ > t₁>0, то log_a t₁- log_a t₂ > 0. При a <1 a-1< 0 и если t₁>t₂, то (a-1)(t₁-t₂) <0, а если t₂>t₁, то (a-1)(t₁-t₂) >0, т.е. знак выражения

log_a t₁- log_a t₂ совпадает со знаком выражения (a-1)(t₁-t₂).

 

 

17. При каких значениях параметра a неравество 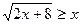и уравнение

равносильны?

 

Решение 1

Решим неравенство 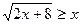. При x < 0 решениями неравенства будут все x, принадлежащие области допустимых значений: 2x + 8 ≥0, т.е.[-4;0).

При x ≥ 0 возведем обе части неравенства в квадрат: 2x + 8 ≥ x².

Откуда x² -2x-8 ≤ 0 или (x-4)(x+2) ≤ 0, тогда x . Объединив полученные результаты, получаем x . Значит решением уравнения должны быть любые значения x, изпромежутка [-4;4].

Найдем «подозрительные» значения параметра a, потребовав чтобы уравнение обращалось в верное равенство при некотором «удобном» значении x из отрезка [-4;4].

Положив x=0, получим │a│+4 = 8, откуда a = ± 4. Таким образом, если уравнение и имеет решением отрезок [-4;4], то только при a = ± 4.Провери эти значения a. При a = 4 уравнение имеет вид 2│x+4│=8, т.е.x₁=0; x₂ =-8,

Cледовательно, a = 4 не является решением задачи.

При a = -4 имеем .

Решая последнее уравнение методом интервалов, получим:

a)при x <-4: -x + 4 - x- 4 = 8: x= -4 (-∞; -4), т.е. если x < -4, то уравнение решений не имеет.

б)при x : -x + 4 + x+4 = 8. Так как полученное равенство является тождеством, то решением является весь отрезок.

в) при x >4: x - 4 + x + 4 = 8: x =4 (4;+ ∞), т.е. если x >4, то уравнение решений не имеет.

Итак, при a = -4 решением уравнения является отрезок [-4;4], т.е. a=-4 – решение задачи.

Ответ: a =-4

 

Решение 2

 

Решим неравенство 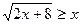. Для этого построим графики функций

f(x) = 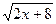, и g(x) = x.

График f(x) = получен параллельным переносом графика функции y = на 4 единицы влево вдоль оси оX.

График g(x) = x- прямая, проходящая через начало координат.

Ясно, что решениями неравенства будут те значения x, для которых первый график расположен выше второго, т.е. x .

График левой части уравнения , т.е. функции h(x) =│x+a│+│x+4│ представляет собой объединение двух лучей и отрезка

длины │a-4│, параллельного оси OX и проходящего через точку (0; │a-4│), Для того, чтобы решением данного уравнения был отрезок

необходимо, чтобы │a-4│=8, а для того, чтобы отрезок имел концы в точках -4 и 4 достаточно, чтобы a = -4.

Ответ: a =-4

 

18. Найдите количество целых решений неравенства

log_2+x (6-│x│) ≥ 0

 

Решение 1

Перепишем данное неравенство, заменив значение 0 на log_2+x 1, получим

log_2+x (6-│x│) ≥ log_2+x1.

Следует учитывать, что логарифмическая функция y = log_a x возрастает

при a >1 и убывает при 0 < a <1. Поэтому от исходного неравенства перейдем к двум системам:

или

 

Целыми числами неравенства являются: 0,1,2,3,4,5.

Ответ: 6.

 

Решение 2

 

Заметим, что целые числа из области определения функции

y = log_2+x (6-│x│) – это числа от нуля до шести (включая ноль и не включая шесть). Действительно, условия x + 2 > 0, x+2 ≠ 1, 6-│x│> 0 определяют эти целые числа. При этих x функция y = log_2+x (6-│x│) убывает, а так как при x=5 значение функции равны нулю, то при x < 5 log_2+x (6-│x│) > 0.

Т.е. целые решения – это целые числа из области определения функции:

0;1;2;3;4;5;

Ответ: 6

 

 

19. Решите уравнение:

.

В ответ запишите количество корней на промежутке

[0;2π]

 

 

Решение 1

,

 

Таким образом, система уравнений распадается на две системы:

, или ,

,

 

,

 

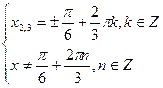Используя тригонометрический круг единичного радиуса, найдем корни уравнения, принадлежащие заданному в условии промежутку [0; 2π]

Такими корнями являются числа В ответе запишем количество корней.

Ответ: 3

 

Решение 2

 

Заметим, что отрезок [0;2π] имеет длину периода функции, стоящей в левой части данного уранения. Поэтому решим уравнение на этом периоде.

 

 

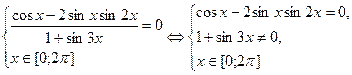
К произведению 2sinx·sin2x

применим формулу произведения синусов: 2sinxsin2x = сosx-cos3x, получим систему,равносильную предыдущей:

Ответ: 3

 

20. Решить уравнение

 

2

 

Решение 1

 

Используя метод возведения обеих частей уравнения в одну и туже степень, решим данное иррациональное уравнение:

О.Д.З. x

 

Проверка:

Значит, значение x =7 является корнем уравнения.

 

Ответ: 7

 

Решение 2

Заметим, что функция y =2 возрастает на всей области определения, поэтому, если данное уравнение имеет корень, то только один.

Поищем его среди целых чисел, не больших 7. Как раз 7 – подходит, по теореме о корне – 7 – единственный корень данного уравнения.

Ответ: 7

 

21. Дано двузначное число. Число его единиц на 3 меньше числа десятков. Произведение этого числа на число, записанное теми же цифрами в обратном порядке, равно 574. Найдите это число.

 

Решение1

Пусть x – цифра десятков этого числа, y – цифра единиц, тогда по условию

задачи получаем уравнение x - y =3. Данное число имеет вид 10 x + y,

число, записанное этими же цифрами, но в обратном порядке имеет вид

10 y + x. Тогда по условию задачи имеем уравнение:

(10 x + y) (10 y + x)=574. Имеем систему:

 

Решая эту систему, получим x = 4, y = 1.

 

Ответ: 41

 

Решение 2

Представим число 574 в виде произведения двух двузначных чисел.

574 = 2·7·41= 14·41 – и это единственный способ разложения этого числа на

произведение двух двузначных чисел. При этом число единиц у 41 на 3 меньше числа десятков. Значит, число 41 – искомое.

Ответ: 41

 

 

22. Найти натуральные числа, образующие арифметическую прогрессию, если произведение трех и четырех первых ее членов равны соответственно 6 и 24.

 

Решение 1

По условию задачи a₁ a₂ a₃ = 6, a₁ a₂ a₃a₄ = 24. Разделим второе уравнение на первое, получим, что четвертый член равен a₄ = 4, или 4 = a₁+3d, откуда

a₁ = 4 - 3d. Подставим выражение для a₁ в первое уравнение, получим:

(4-3d)(4-2d) (4-d) =6 или (4-3d)(2-d) (4-d) =3 или -3d³ +22d² -48d +29 = 0,

решая это уравнение, получим d = 1. Тогда a₁ = 4 - 3d =1, a₂ =2, a₃ = 3.

Ответ: 1; 2;3.

Решение 2

Очевидно, что число 6 может быть представлено в виде произведения трех натуральных чисел только двумя различными способами: 1·2·3 и 1·1·6.

Но числа 1, 1, 6 не являются членами арифметической прогрессии, а числа 1,2,3, записанные в указанном порядке, являются членами арифметической прогрессии. Как видно, второе условие, касающееся произведения четырех

членов является даже лишним.

Ответ: 1; 2;3.

 

23. После деления некоторого двузначного числа на сумму его цифр в частном получается 7 и в остатке 6. После деления этого двузначного числа на произведение его цифр в частном получается 3 и в остатке 11. Найдите это двузначное число.

 

Решение 1

Пусть x – число десятков искомого числа, y – число единиц. Тогда данное

число имеет вид: 10x + y. Так как после деления некоторого двузначного числа на сумму его цифр в частном получается 7 и в остатке 6, то

10x + y = 3x·y + 11

 

После деления этого двузначного числа на после деления этого двузначного числа на произведение его цифр в частном получается 3 и в остатке 11, то

10x + y = 7(x+y) + 6.

Решим систему:

Так как x и y – это цифры числа, то подходят только значения x=8; y=3.

Искомое число 83.

Ответ: 83.

Решение 2

Обозначим x и y соответственно число десятков и число единиц данного числа, тогда по второму условию 10x + y = 3xy + 11. Из этого равенства выразим x = , так как x и y – это цифры числа, то у может принимать только значения 0, 1, 2, 3. Подставляя в это равенство указанные значения, получим, что только при y = 3, получается натуральное число x=8.

Следовательно, 83- искомое число. Как видно, первое условие

является даже лишним.

Ответ: 83.

 

 

24. Два велосипедиста выехали одновременно из пунктов A и B навстречу друг другу и встретились в 70 км от А. Продолжая движение с теми же скоростями, они достигли конечных пунктов и, отдохнув равное время, вернулись назад. Вторая встреча произошла в 90 км от B. Найдите расстояние от A до B.

Решенеие 1

Пусть расстояние между городами S. Cорость первого велосипедиста x,

второго - y. Время движения первого велосипедиста до первой встречи

второго . По условию задачи получаем уравнение: .

Расстоянине, пройденное первым велосипедистом до второй встречи равно

s+90, а вторым – 2s - 90 Время движения первого велосипедиста до

второй встречи второго . По условию задачи получаем уравнение: . Из каждого уравнения выразим отношения:

и 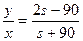. Далее .

Решая это уравнение, получим s = 0, s =120. По условию задачи подходит только корень s=120.

Ответ: 120 км

 

 

Решение 2

 

К моменту первой встречи оба велосипедиста вместе проехали расстояние AB, а к моменту второй встречи – вместе проехали расстояние, втрое большее,чем AB. Так как скорости велосипедистов не менялись, то и каждый из них до второй встречи проехал расстояние, втрое большее, чем AB. Так как первый велосипедист до первой встречи прехал 70 км, следовательно, первый велосипедист до второй встречи проехал расстояние

70·3 =210 (км). А так как вторая встреча произошла в 90 км от B, то расстояние от A до B равно 210 – 90 = 120(км).

Ответ: 120 км.

 

25. Найдите четырехзначное число по следующим данным:

cумма квадратов крайних цифр равна 13, сумма квадратов средних цифр равна 85; если из искомого числа вычесть 1089, то получится число, написанное теми же цифрами в обратном порядке.

 

Решение 1

Пусть x, y, z, t – цифры тычяч, сотен, десятков и единиц соответственно данного числа, тогда данное число имет вид 1000 x+ 100y + 10z +t.

По условию задачи составим уравнения: x² + t² =13, y² +z² = 85,

1000 x+ 100y + 10z +t – 1089 =1000 t+ 100z + 10y +x.

Последнее уравнение приведем к виду: 111(x-t) +10(y-z) = 121.

Ясно, что 0 < x-t ≤ 2, т.е. x-t =1, откуда x = t + 1 или x-t =2.

Рассматривая эти два случая с двумя другими уравнениями системы, получим x = 3, t = 4, y = 7, z = 6. Тогда искомое число 3762.

Ответ: 3762.

 

 

Решение 2

 

Учитывая, что цифры числа – неотрицательные целые числа, не большие, чем 9, получим, что такими крайними цифрами могут быть только 2 и 3,

(только 2²+3² =13), а средние 9 и 2 или 7и 6. По условию цифра тысяч больше цифры единиц, а цифра сотен больше цифры десятков. Значит искомое число 3922 или 3762.

 

Непосредственная проверка последнего условия показывает, что ему удовлетворяет только второе число.

Ответ: 3762.

 

26. Упростите выражение:

tg20˚+tg40˚+√3tg20˚tg40˚

 

Решение 1

tg20˚+tg40˚+√3tg20˚tg40˚ =

=

 

Решение 2

Заметим, что из формулы тангенса суммы

tg20˚+tg40˚=tg(20˚+40˚)(1-3tg20˚tg40˚), тогда

tg20˚+tg40˚+√3tg20˚tg40˚ = tg(20˚+40˚)(1-tg20˚tg40˚)+√3tg20˚tg40˚ =

 

tg(60˚)(1-tg20˚tg40˚)+√3tg20˚tg40˚ = √3 -√3tg20˚tg40˚ +√3tg20˚tg40 =√3.

 

27. Если 4^x + 4^-x =3, то величина 64^x + 64^-x равна

 

1) 27; 2) 18; 3) 9; 4)24; 5)36

Решение 1

Чтобы н

⇐ Предыдущая123456

Поделиться:

Воспользуйтесь поиском по сайту: