 |
Ошибки в тождественных преобразованиях выражений, содержащих логарифмы.
|
|
|
|
1. Если n  N, то logab2n ≠2nlogab.
N, то logab2n ≠2nlogab.
Ошибка в том, что равенство logab2n =2nlogab справедливо только для b>0. Если b<0, то
logab2n =2nloga (-b).
Вообще говоря, справедливо равенство: logab2n =2nloga ׀ b ׀.
2. log2 22x ≠1+ log2 2x.,
Правильное решение:
log2 22x = (log22+ log2 x)2 =(1+ log2 x)2 = 1+ 2log2 x+ log2 2x.
3.  .,
.,
Пправильное решение:  , так как по формуле перехода от одного основания к другому получим:
, так как по формуле перехода от одного основания к другому получим:  , а затем применим основное логарифмическое тождество.
, а затем применим основное логарифмическое тождество.
.
4.Упростите выражение:  при условии, что x >y.
при условии, что x >y.
 .
.
Правильное решение:
 =
=
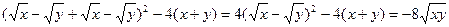
4.
Раздел 32
Ошибки при решении уравнений
| Задание 1 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите уравнение  . .
| числа 1 и 2 - корни | 2 – посторонний корень | корень уравнения - число 1. | Неверно применяется условие равенства произведения двух множителей нулю: произведение двух множителей равно нулю, если хотя бы один из множителей равен нулю, а другой при этом не теряет смысла. |
| Решение | 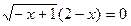   x=1 x=1
| |||
| Для справки | Условие равенства нулю произведения нескольких множителей: для того,чтобы произведение нескольких множителей равнялось нулю, достаточно, чтобы хотя бы один из них равнялся нулю, а другие при этом не теряли смысла. |
Упражнение 1
Решите уравнение:  .
.
| Задание 2 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите уравнение 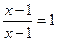 . .
| x 
| x=1- не корень уравнения | 
| Не учтено условие существования дроби 
|
| Решение | 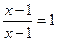  
| |||
| Для справки |
|
1.Решите уравнение  . Ответ: числа 1 и 2 корни уравнения – неверный. Правильное решение – корень уравнения только число 1.
. Ответ: числа 1 и 2 корни уравнения – неверный. Правильное решение – корень уравнения только число 1.
|
|
|
Число x = 2 не является корнем уравнения, так как при x = 2 выражение
 не определено. Неверно применяется условие равенства произведения двух множителей нулю: произведение двух множителей равно нулю, если один из множителей равен нулю, а другой при этом не теряет смысла.
не определено. Неверно применяется условие равенства произведения двух множителей нулю: произведение двух множителей равно нулю, если один из множителей равен нулю, а другой при этом не теряет смысла.
Упражнение 2
Решите уравнение  .
.
2.Решите уравнение 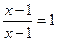 . Ответ: х - любое число – неверный.
. Ответ: х - любое число – неверный.
Правильный ответ  , так как при x=1 дробь
, так как при x=1 дробь  не определена.
не определена.
| Задание 3 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите уравнение  . .
| x=1 | x=1- не корень уравнения | Корней нет | Не учтено условие существование дроби 
|
| Решение |   x x  Ø Ø
|
Упражнение 3
Решите уравнение  .
.
3.Решите уравнение  . Ответ: х =1 – неверный, так как при x =1
. Ответ: х =1 – неверный, так как при x =1
дробь  не определена. Неверно применено условие равенства дроби нулю: дробь равна нулю, если числитель этой дроби равен нулю, а знаменатель не равен нулю.
не определена. Неверно применено условие равенства дроби нулю: дробь равна нулю, если числитель этой дроби равен нулю, а знаменатель не равен нулю.
Правильный ответ: корней нет.
| Задание 4 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите уравнение  . .
| Корни: 3;0;-3 | x = 0- не корень уравнения | Корни: 3;-3 | Не учтено условие существования дроби 
|
| Решение |    
|
Упражнение 4
Решите уравнение  .
.
4.Решите уравнение  Ответ: 0; 3 - неверный.
Ответ: 0; 3 - неверный.
Правильный ответ: 3, -3, так как при x = 0 дробь 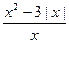
не определена - знаменатель этой дроби равен нулю.
| Задание 5 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите уравнение 
| Корни: 2; 3 | x=2- не корень уравнения | Корень уравнения x = 3 | Не учтено условие существования корня |
| Решение: |   x =3 x =3
|
Упражнение 5
Решите уравнение  .
.
5. Решите уравнение  . Ответ: 2; 3 - неверный. Правильный ответ: 3, так как при x = 2 дробь
. Ответ: 2; 3 - неверный. Правильный ответ: 3, так как при x = 2 дробь  не определена – корень из отрицательного числа не существует.
не определена – корень из отрицательного числа не существует.
6. Решите уравнение: (x-3)(x2 +1) =2(x-3)
, ответ: 1; -1 – неверный.
Правильный ответ: 3; 1; -1.Ошибка в том, что был потерян корень при делении обеих частей уравнения на выражение x-3, которое обращается в ноль при х=3, а значит число 3 служит корнем уравнения (x-3)(x2 +1) =2(x-3).
|
|
|
| Задание 6 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите уравнение (x-3)(x2 +1) =2(x-3) | Корни:-1; 1 | Потерян корень уравнения x=3 | Корни уравнения: -1;1;3 | Потерян корень при делении обеих частей уравнения на выражение x-3, которое обращается в ноль при х = 3, число 3 служит корнем уравнения (x-3)(x2 +1) =2(x-3). |
| Решение: | (x-3)(x2 +1) =2(x-3)  ((x-3)(x2 -1=0) ((x-3)(x2 -1=0) 
|
Упражнение 6
Решите уравнение: (x-6)(x2 - 3) =(x-6).
7. Решите уравнение: ׀x-10 ׀(log2(x-3)) = 2(x-10).
Ответ: 7; 10; 3,25 – неверный.
Правильный ответ: 10; 3,25. Ошибка в том, что корень 7 был найден при
условии x > 10 и этому условию не удовлетворяет.
| Задание 7 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите уравнение │x-10│· ·(log2(x -3)) =2(x-10) | Корни: 7; 10; 3,25 | Число 7-не корень | Корни уравнения: 10; 3,25. | Корень 7 был найден при условии x > 10 и этому условию не удовлетворяет. |
| Решение: | │x-10│ (log2(x -3)) =2(x-10)   
|
Упражнение 7
Решите уравнение: ׀x - 1׀(log2(x-2)) = x-1.
8. Решите уравнение x2 + ׀x-1 ׀= 3, ответ:  , -1, 2 – неверный. Правильный ответ -1;
, -1, 2 – неверный. Правильный ответ -1;  . Ошибка в том, что при снятии модуля получаются уравнения, корни которых должны удовлетворять условиям: в одном случае x ≥ 1; в другом случае x <1, корень
. Ошибка в том, что при снятии модуля получаются уравнения, корни которых должны удовлетворять условиям: в одном случае x ≥ 1; в другом случае x <1, корень  был найден при условии x ≥ 1 и этому условию не удовлетворяет.
был найден при условии x ≥ 1 и этому условию не удовлетворяет.
| Задание 8 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите уравнение x2 + ׀x-1 ׀= 3 | Корни:
 ;
-1; 2 ;
-1; 2
|  -
не корень -
не корень
| Корни уравнения:
-1;  . .
| Корень  был найден при условии x ≥ 1 и этому условию не удовлетворяет, а корень 2 найден при условии x <1 и этому условию не удовлетворяет был найден при условии x ≥ 1 и этому условию не удовлетворяет, а корень 2 найден при условии x <1 и этому условию не удовлетворяет
|
| Решение | x2 + ׀x-1 ׀= 3  
|
Упражнение 8
Решите уравнение x2 + ׀x+1 ׀= 2.
9. Решите уравнение 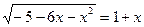 (1). Ответ: -1; 2 – неверный.
(1). Ответ: -1; 2 – неверный.
Правильный ответ: -1. Ошибка в том, что x =2 – посторонний корень,
получен при решении уравнения 5-x2 = (1-x)2 (2), неравносильного данному.
Следует проверить условие 1-x ≥ 0, поскольку только при этом условии
уравнения (1) и (2) равносильны.
| Задание 9 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите уравнение

| Корни: -1; 2 | 2- не корень | Корень уравнения: -1 | x =2 – посторонний корень, получен при решении уравнения 5-x2 = (1-x)2 неравносильного данному. |
| Решение |   5-x2 = (1-x)2 5-x2 = (1-x)2  .
Проверка: x=-1, .
Проверка: x=-1,  равенство верное, значит x=2 – корень данного уравнения.
x=2, равенство верное, значит x=2 – корень данного уравнения.
x=2,  равенство неверное, значит x=2 – не корень данного уравнения. равенство неверное, значит x=2 – не корень данного уравнения.
|
|
|
|
Упражнение 9
Решите уравнение 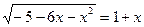
10. Решите уравнение (x-4) log2(1-x) = 0.
Ответ: 4; 0 – неверный.
Правильный ответ: корень уравнения - 0. Ошибка в том, что x = 4
не удовлетворяет условию существования логарифма:
1-x > 0, т.е. при х = 4 первый множитель равен нулю, а второй при этом
значении переменной не имеет смысла.
| Задание 10 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите уравнение (x-4) log2(1-x) = =0 | Корни: 4; 0 | 4- не корень | Корень уравнения 0 | x = 4 не удовлетворяет условию существования логарифма: 1-x > 0, при х = 4 первый множитель равен нулю, а второй при этом значении переменной не имеет смысла. |
| Решение |
(x-4) log2(1-x) = 0 
|
Упражнение 10
Решите уравнение (x2-4) log2(2-x) = 0.
11. Решите уравнение  . Ответ: x =1 – неверный. Решение: переход от данного уравнения к уравнению
. Ответ: x =1 – неверный. Решение: переход от данного уравнения к уравнению  не равносилен. Корни первого уравнения 1 и -1, а второе уравнение имеет только один корень 1, так как по определению степени с дробным показателем основание степени положительно и не равно 1. Правильный ответ: 1 и -1.
не равносилен. Корни первого уравнения 1 и -1, а второе уравнение имеет только один корень 1, так как по определению степени с дробным показателем основание степени положительно и не равно 1. Правильный ответ: 1 и -1.
| Задание 11 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите уравнение

| Корень: | Потерян корень x=-1 | Корни уравнения: 1 и -1 | Переход от данного уравнения к уравнению  не равносилен. Корни данного уравнения 1 и -1, а второе уравнение имеет только один корень 1, так как по определению степени с дробным показателем основание степени положительно.
. не равносилен. Корни данного уравнения 1 и -1, а второе уравнение имеет только один корень 1, так как по определению степени с дробным показателем основание степени положительно.
.
|
| Решение |  
|
Упражнение 11
Решите уравнение  .
.
12. Решите уравнение 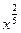 =1. Ответ: х = 1; -1 неверный. Правильное решение
=1. Ответ: х = 1; -1 неверный. Правильное решение
x =1, так как по определению степени с дробным показателем основание
степени положительно и не равно 1
.
| Задание 12 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите уравнение
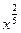 =1 =1
| Корни: 1 и -1. | x=-1- не корень | Корень уравнения: 1 | Переход от данного уравнения к уравнению  не равносилен. Корень данного уравнения =1, так как по определению степени с дробным показателем основание степени положительно. а второе уравнение имеет корени 1 и -1. не равносилен. Корень данного уравнения =1, так как по определению степени с дробным показателем основание степени положительно. а второе уравнение имеет корени 1 и -1.
|
| Решение: | 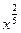 =1 =1 
|
|
|
|
Упражнение 12
Решите уравнение 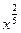 =4.
=4.
13. Решите уравнение  .
.
Ответ: x = 3 – неверный. Правильное решение: x = 3, x = -1, x = 1, так как корень x = 3 получен при условии x > 0, x ≠1,
но по определению степени с целым показателем основание степени может быть равным 1 и отрицательному числу. Проверяем 1, получаем 11-4 = 1, т.е.
1 – корень уравнения. Среди отрицательных чисел только -1 в четной степени равняется 1. Поэтому возможный отрицательный корень -1.
Проверим: получим (-1)-1-3 = 1, значит x = -1 – корень уравнения.
| Задание 13 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите уравнение
 . .
| Корень: | Потеряны корни 1 и -1 | Корни уравнения: -1; 1;3. | Корень x = 3 получен при условии x > 0, x ≠1, по определению степени с целым показателем основание степени может быть равным 1 и отрицательному числу |
| Решение | При условии x > 0, x ≠1, имеем  0, откуда x =3
По определению степени с целым показателем основание степени может быть равным 1 и отрицательному числу. Проверяем 1, получаем 11-4 = 1, т.е.
1 – корень уравнения. Среди отрицательных чисел только -1 в четной степени равняется 1. Поэтому возможный отрицательный корень -1.
Проверим: получим (-1)-1-3 = 1, значит x = -1 – корень уравнения. 0, откуда x =3
По определению степени с целым показателем основание степени может быть равным 1 и отрицательному числу. Проверяем 1, получаем 11-4 = 1, т.е.
1 – корень уравнения. Среди отрицательных чисел только -1 в четной степени равняется 1. Поэтому возможный отрицательный корень -1.
Проверим: получим (-1)-1-3 = 1, значит x = -1 – корень уравнения.
  
|
Упражнение 13
Решите уравнение  .
.
14. Решите уравнение x2 -1 = (x - 1)  .
.
Ответ: x = -5, x =1 неверные. Правильный ответ: уравнение не имеет
корней.
Ошибки: при x =1 не выполняется условие существования квадратного
корня x2 – 9 ≥ 0; при x = -5 левая часть уравнения положительна, а
правая – отрицательна.
| Задание 14 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите
уравнение
x2 -1 =
(x-1)  . .
| Корни: 1 и -5. | x=1 и x=-5 – посторонние корни | Корней нет | При x =1 не выполняется условие существования квадратного корня x2 – 9 ≥ 0; при x = -5 левая часть уравнения положительна, а правая – отрицательна. |
| Решение | x2 -1 = (x - 1)  
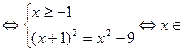 Ø Ø
|
Упражнение 14
Решите уравнение x2 -16 = (x - 4)  .
.
15. Решите уравнение: x2 -1 = (x - 1)  .
.
Ответ: x = 4 - неверный. Правильный ответ: корни уравнения 4 и 1. Потеря корня x = 1 произошла при делении обеих частей уравнения на x-1. Это выражение обращается в ноль при x =1, а поэтому х =1 корень данного уравнения
.
| Задание 15 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите уравнение
x2 -1 =
(x - 1)  . .
| Корень | Потерян корень x=1 | Корни уравнения 4 и 1 | Потеря корня x = 1 произошла при делении обеих частей уравнения на x-1. Это выражение обращается в ноль при x =1, х =1 корень данного уравнения. |
| Решение | x2 -1 = (x - 1) 

|
|
|
|
Упражнение 15
Решите уравнение: 4x2 -1 = (2x - 1)  .
.
16. Решите уравнение lg x2 = 4. Ответ x = 100 – неверный. Правильный ответ
x=100 и x = -100. Ошибка в применении формулы lg x2 = 2lgx. Эта
формула верна только при x > 0. Если же x < 0, то lg x2 = 2lg(-x), поэтому
второй корень получен из уравнения lg(-x) = 2, а первый из уравнения
lgx = 2.
| Задание | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите уравнение lg x2 = 4 | Корень: | Потерян корень x =-100 | Корни уравнения 100 и -100 | Ошибка в применении формулы lg x2 = 2lgx. Эта формула верна только при x > 0. Если же x < 0, то lg x2 = 2lg(-x), поэтому второй корень получен из уравнения lg(-x) = 2, а первый из уравнения lgx = 2. |
| Решение | lg x2 = 4  2lg│x│=4 2lg│x│=4  lg│x│=2 lg│x│=2  │x│=100 │x│=100  
|
Упражнение 16
Решите уравнение lg x2 = 6.
17. Решите уравнение sin x tg 0,5x = 0. Ответ: x = πn, n  неверный.
неверный.
Правильное решение x =2πn, n  . Ошибка в том, что при x = πn первый
. Ошибка в том, что при x = πn первый
множитель равен нулю, а второй при этом значении переменой не
определен, если n – нечетное целое число.
| Задание 17 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите уравнение sin x· ·tg0,5x= 0. | x = πn, n 
| Посторонние решния x=π(2k+1), n  . .
| x=2πn, n  . .
| Неверно применяется условие равенства произведения двух множителей нулю: при x = πn первый множитель равен нулю, а второй при этом значении переменой не определен, если n – нечетное целое число. |
| Решение | sin x tg0,5x = 0   x =2πn, n x =2πn, n  . .
|
Упражнение 17
Решите уравнение sin2x x tg x = 0.
18. Решите уравнение sinx =-2. Ответ  где
где  -
-
неверный.
Правильный ответ: это уравнение не имеет корней, так как множество
значений синуса отрезок [-1;1].
| Задание 18 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите уравнение sinx =-2 |  где где 
| Не существует arcsin(-2) | Уравнение не имеет корней | Это уравнение не имеет корней, так как множество значений синуса отрезок [-1;1]. |
| Решение | sinx =-2, так как E(sinx) = [-1;1], то данное уравнение не имеет решения. | |||
| Для справки | Уравнение sinx = a, x- неизвестная переменная, a-некоторое постоянное число.
а)Если a>1 или a< -1, то уравнение sinx = a не имеет решений.
Например, уравнения sinx = 4, sinx = -2,4 не имеют решений.
б)Ecли a= 1, то решение уравнения: x=  в) Ecли a= -1, то решение уравнения: x= -
в) Ecли a= -1, то решение уравнения: x= -  г) Ecли a= 0, то решение уравнения: x=
г) Ecли a= 0, то решение уравнения: x=  д) Ecли |a|
д) Ecли |a|  то x=(-1)narcsina+πn, n то x=(-1)narcsina+πn, n 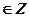 .
Например, решение уравнения sinx = 0,3 записывается в виде
x=(-1)narcsin0,3+πn, n .
Например, решение уравнения sinx = 0,3 записывается в виде
x=(-1)narcsin0,3+πn, n 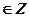 .
Уравнение соsx = a, x- неизвестная переменная, a-некоторое постоянное число.
а)Если a>1 или a< -1, то уравнение cosx = a не имеет решений.
Например, уравнения cosx = 1,4, sinx = -2,5 не имеют решений.
б)Ecли a = 1, то решение уравнения: x= .
Уравнение соsx = a, x- неизвестная переменная, a-некоторое постоянное число.
а)Если a>1 или a< -1, то уравнение cosx = a не имеет решений.
Например, уравнения cosx = 1,4, sinx = -2,5 не имеют решений.
б)Ecли a = 1, то решение уравнения: x=  в) Ecли a= -1, то решение уравнения: x=
в) Ecли a= -1, то решение уравнения: x=  г) Ecли a= 0, то решение уравнения: x=
г) Ecли a= 0, то решение уравнения: x=   д) Ecли a
д) Ecли a  то x= то x= 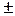 arccosa+2πn, n arccosa+2πn, n 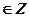 .
Например, решение уравнения cosx = 0,3 записывается в виде
x= .
Например, решение уравнения cosx = 0,3 записывается в виде
x= 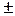 arccos0,3+2πn, n arccos0,3+2πn, n 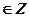 .
Уравнение tgx = a, x- неизвестная переменная, a-некоторое постоянное число.
Решение уравнения x=arctga + πn, n .
Уравнение tgx = a, x- неизвестная переменная, a-некоторое постоянное число.
Решение уравнения x=arctga + πn, n 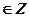 .
Например, решение уравнения tgx=3, будет x=arctg3 + πn, n .
Например, решение уравнения tgx=3, будет x=arctg3 + πn, n 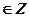 .
Замечание: если a=0, то x= πn, n .
Замечание: если a=0, то x= πn, n 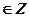 . .
|
Упражнение 18
Решите уравнение sin 5x = 5.
19. Решите уравнение sin2x – sinxcosx = 0. Ответ: x = π/4+πn, n  - неверный. Правильный ответ: x = π/4+πn, n
- неверный. Правильный ответ: x = π/4+πn, n  , x = πk, k
, x = πk, k  .
.
Ошибка – в делении обеих частей уравнения на sinx.
При x = πk, n  sinx = 0 и уравнение обращается в верное равенствот.е.
sinx = 0 и уравнение обращается в верное равенствот.е.
x = πk, k  - решение данного уравнения.
- решение данного уравнения.
| Задание 19 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите уравнение sin2x – sinxcosx = 0 | x = π/4+πn, n 
| Потеряно
решение
x = πk, k 
| x =π/4+πn, n  ,
x = πk, k ,
x = πk, k  . .
| в делении обеих частей уравнения на sinx.
При x = πk, n  sinx = 0 и уравнение обращается в верное равенствот.е.
x = πk, k sinx = 0 и уравнение обращается в верное равенствот.е.
x = πk, k  - решение данного уравнения. - решение данного уравнения.
|
| Решение | sin2x – sinxcosx=0 
|
Упражнение 19
Решите уравнение cos2x – sinxcosx = 0.
20. Решите уравнение: tg3x= tg 5x. Ответ x = πk/2, k  - неверный. Правильный ответ: x = πn, n
- неверный. Правильный ответ: x = πn, n  . Ошибка в том, что не при всех x из серии
. Ошибка в том, что не при всех x из серии
x = πk/2, k  определены tg3x и tg 5 x (иначе – не все корни из серии
определены tg3x и tg 5 x (иначе – не все корни из серии
x = πk/2, k  входят в ОДЗ данного уравнения). Следует исключить те значения x при которых соs3x и сos5x обращаются в ноль, это происходит при нечетных k. Исключая нечетные k, получим правильный ответ x = πn, n
входят в ОДЗ данного уравнения). Следует исключить те значения x при которых соs3x и сos5x обращаются в ноль, это происходит при нечетных k. Исключая нечетные k, получим правильный ответ x = πn, n  .
.
| Задание 20 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите уравнение tg3x= tg 5x | x = πk/2, k 
|
Постороннее решение
x =π/2+ πk, k 
| x = πn, n  . .
| Не при всех x из серии
x = πk/2, k  определены tg3x и tg5x (иначе – не все корни из серии
x = πk/2, k определены tg3x и tg5x (иначе – не все корни из серии
x = πk/2, k  входят в ОДЗ данного уравнения). входят в ОДЗ данного уравнения).
|
| Решение | tg3x= tg 5x   
   x = πn, n x = πn, n  . .
| |||
| Для справки | Условие равенства тангенсов двух углов:
tgα = tg β 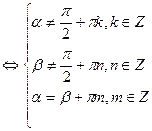
|
Упражнение 20
Решите уравнение: tg2x= tg 6x.
| Задание 21 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите уравнение сos4x = 0,5 | x= 
| Неверно найдено второе слагаемое | 
| Для отыскания x в левой части равенства только первое слагаемое разделили на 4. |
| Решение | сos4x = 0,5  4x = 4x =    ,
x = ,
x = 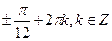
|
Упражнение 21
Решите уравнение tg 4x = 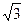
| Задание 22 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите уравнение cosx+sinx =1 | x = πn/2, n 
| Посторонние решения:
x = π+ 2πn, n  ,
x = -π/2+ 2πk, k ,
x = -π/2+ 2πk, k  . .
| x =2πn, n  ,
x = π/2+ 2πk, k ,
x = π/2+ 2πk, k  . .
| Метод решения заключался в возведении обеих частей уравнения в квадрат, т.е. от данного уравнения перешли к уравнению - следствию sin 2x = 0, не все корни которого являются корнями данного. |
| Решение | sin x + cos x = 1(1).Поскольку период функциии y= sin x + cosx равен 2π, то найдемрешения уравнения (1) на этом периоде, например на отрезке [0; 2π ] Поскольку │sinx│≤1 и │cosx│≤1, и для x из промежутка (π/2; 2π) по крайней мере, одна из функций (синус или косинус) неположительна и не принимает значения, равные 1, то в этом интервале рашений нет. На оставшемся отрезке [0; π/2 ] очевидные решения x = 0, x = π/2, других решений на интервале (0; π/2) нет, поскольку значения синуса и косинуса на этом интервале численно равны катетам прямоугольного треугольника, гипотенуза которого равна 1.
С учетом периода решения данного уравнения: x =2πn, n  , x= π/2+ 2πk, k , x= π/2+ 2πk, k  . .
|
Упражнение 22
Решите уравнение 3sin x + cos x = 1.
| Задание 23 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите уравнение 2sin x + cos x = 1. | x = π k,  . .
| На cos x разделили только левую часть данного уравнения. | x=(-1)k arcsin  - arctg 0,5 + πk, - arctg 0,5 + πk,  . .
| При решении уравнения 2sinx +cosx = 1 получают  , это не-верно.
Уравнение 2sinx +cosx = 1 – не однородное относительно sinx и cosx, поэтому деление на соsx, при том только левой части уравнения- грубая ошибка. , это не-верно.
Уравнение 2sinx +cosx = 1 – не однородное относительно sinx и cosx, поэтому деление на соsx, при том только левой части уравнения- грубая ошибка.
|
| Решение | 2sin x + cos x = 1    x=(-1)k arcsin
x=(-1)k arcsin  - arctg 0,5 + πk, - arctg 0,5 + πk,  . .
| |||
| Для справки | Уравнение вида asinx+bcosx=c
Чтобы решить уравнение такого вида (например,
3sin x + 4cos x =2), можно:
1.Записать его в виде sin(x +t) = 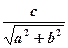 (в нашем случае
sin(x +t) = (в нашем случае
sin(x +t) =  , sin(x +t) = , sin(x +t) = 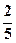 ).
2.Решить простейшее тригонометрическое уравнение:
sin(x +t) = ).
2.Решить простейшее тригонометрическое уравнение:
sin(x +t) = 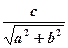 (в нашем случае sin(x +t) =
(в нашем случае sin(x +t) = 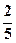 , x+t =(-1)karcsin 0,4 +πk, , x+t =(-1)karcsin 0,4 +πk,  ;
x = (-1)k arcsin 0,4 – t + πk, ;
x = (-1)k arcsin 0,4 – t + πk,  );
3. Определить t, t = arctg b/a (в нашем случае t = arctg4/3);
4. Записать ответ: x = (-1)k arcsin 0,4 – arctg4/3+πk, );
3. Определить t, t = arctg b/a (в нашем случае t = arctg4/3);
4. Записать ответ: x = (-1)k arcsin 0,4 – arctg4/3+πk,  . .
|
Упражнение 23
Решите уравнение sin x - cos x = -1.
21. Решите уравнение: log5(2-x) + log5(-2-x) =1. Ответ: x =  - неправильный
- неправильный
Правильный ответ x = -3.
Ошибка в том, что при переходе от уравнения log5(2-x) + log5(-2-x) =1 к
уравнению log5(2-x) (-2-x)=1 расширяется область определения уравнения
(в данном уравнении ОДЗ: x < -2, а после преобразования О.Д.З. расширяется x < -2, x > 2).
Поэтому x = 3 - посторонний корень.
| Задание 24 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите уравнение log5(2-x) + log5(-2-x) =1 | x = 
| Посторонний корень x=3 | x= -3. | При переходе log5(2-x) + log5(-2-x) =1 к уравнению log5(2-x) (-2-x)=1 расширяется область определения уравнения (в данном уравнении область определения x < -2, а после преобразования –расширяется: x < -2, x > 2). |
| Решение | log5(2-x) + log5(-2-x) =1  log5(2-x) (-2-x)=1 log5(2-x) (-2-x)=1  (2-x) (-2-x)=5 (2-x) (-2-x)=5  x2=9 x2=9  x= x=  3.
Проверка x=3. log5(-2-3) не определен, x=3 – не корень.
x=-3, log5(2-(-3)) + log5(-2-(-3)) =1 - равенство
верно, значит x =-3 – корень уравнения. 3.
Проверка x=3. log5(-2-3) не определен, x=3 – не корень.
x=-3, log5(2-(-3)) + log5(-2-(-3)) =1 - равенство
верно, значит x =-3 – корень уравнения.
|
Упражнение 24
Решите уравнение: log5(4-x2) + log0,2(2-x) =1.
22. Решите уравнение 2x 51/x =2·5. Ответ: x = 1- неверный. Правильный ответ:
корни уравнения: x =1 и x = log2210 -1. Ошибка заключается в том, что из равенства произведений степеней не следует равенство показателей этих степеней, например, 2log28 5 log51,25 =2·5.
| Задание 25 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
| Решите уравнение 2x 51/x=2·5 | x = 1 | Потерян корень log25. | x =1, x = log25 | Из равенства произведений степеней не следует равенство показателей этих степеней, например, 2log28 5 log51,25 =2·5 |
| Решение |
Прологарифмируем левую и правую части уравнения 2x 51/x =2·5
по основанию 2, получим уравненеие, равносильное данному: 
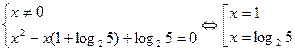
|
Упражнение 25
Решите уравнение 7x 41/x =7·4.
23. Решите уравнение  . Ответ: x = 4, x =284 – неверный.
. Ответ: x = 4, x =284 – неверный.
Правильный ответ: x =284. Ошибка появилась от того, что при возведении обеих частей данного уравнения в квадрат получилось
уравнение – следствие, не все корни которого являются корнями данного уравнения.
При таком методе решения требуется сделать проверку найденных корней.
 , значит, x = 4 не корень данного уравнения.
, значит, x = 4 не корень данного уравнения.  , значит, x =284 корень данного уравнения.
, значит, x =284 корень данного уравнения.
| Задание 26 | Неверный ответ | Ошибка | Верный ответ | Причина ошибки |
Решите уравнение
 . .
| x = 4, x=284 | Посторонний корень x = 4 | x=284. | Ошибка появилась от того, что при возведении обеих частей данного уравнения в квадрат получилось уравнение – следствие, не все корни которого являются корнями данного уравнения. |
| Решение: |  
 
 .
Проверка: .
Проверка:
 , значит, x = 4 не корень данного уравнения. , значит, x = 4 не корень данного уравнения.  , значит, x =284 корень данного уравнения. , значит, x =284 корень данного уравнения.
|
Упражнение 26
Решите ура
|
|
|


