Вычисления, связанные с тригонометрическими функциями

1. Большое число Оошибоки, связанныео с неверным применением формул приведения:

.

а) sin (3π-α) = cosα. Это неверно.

 

Следует помнить, что формулы приведения применяются к тригонометрическим функциям от выражений вида (n + α) или (n - α),где n – целое число. Поэтому аргумент, если это возможно, приводится к такому виду.

 

Следует помнить, что формулы приведения применяются к тригонометрическим функциям от выражений вида (n + α) или (n - α), где n – целое число. В данном случае пПолучимоэтому 3π-α следует привести к такому виду: 3π- α =6 -α. 6 – четное число, поэтому название функции синус не меняется: sin(3π-α) = sinα - это верное решение.

 

б) tg (x - π) = ctgx., Ээто неверно.

Следует аргумент x - π привести к виду

n - α, т.е.. x - π = - ( π-x).

Верно будет: tg(x - π) =- tg( π-x) =-ctgx.

 

Следует помнить, что формулы приведения применяются к тригонометрическим функциям от выражений вида (n + α) или (n - α),где n – целое число. Поэтому аргумент, если это возможно, приводится к такому виду.

 

в) sin () = sinα, sin () = cosα - это неверно выполненные преобразования.

 

Ошибка заключается в том, что применены формулы приведения, которые здесь применить нельзя: числа ,

нельзя представить в виде произведения целого числа n наи числао .

 

 

2. При вычислении значений тригонометрических функций по значению одной из них ошибки допускаются при определении знака значения тригонометрической функции..

 

a) Найдите значение cosx, если

tgx =0,.75, x [π; 3/2π].

 

Ответ: 0,8 - - неверный.

Правильное решение:

Ииз формулы tg²x + 1 = 1/ cos²x найдем

cosx = - , причём знак «-», берется потому, что при x [π; 3/2π] cosx < 0.

 

 

б) Найдите cos (x+y), если cos x = -3/5, а cos y = ⅓, x [ π; 3/2π], y [0; π/2].

 

Ответ cos (x+y) = - 3/5-1/3= -14/15 является неверным.

Правильное решение:

Запишем формулу cos(x+y) = cosx cosy – sinx siny. В правой части этой формулы значения sinx и siny не известны.Найдем их:

sin x = - = , знак «-» ставится потому, что

x [ π; 3/2π], а в третьей четверти косинус отрицательный.

sin y = + = , знак «+» ставится потому, что

y [0; π/2], а в первой четверти синус положительный.

 

Подставим найденные значения в формулу cos(x+y) = cosxcosy – sinx siny, получим: cos(x + y)= .

 

 

3. Большое число ошибок допускается при вычислении значений обратных

тригонометрических функций.

 

 

а) arccos(-0,5)=- 60º- это неверный ответ.

По определению arccosx – это

угол, заключенный в промежутке [0; 180º], поэтому у

arccos(-0,5)=180º-60º=120º - правильный ответ..

 

б) arccoscos 370º = 370º- это неверно найденное значение,

так как хотя и

cos 370º = cosα (arccoscos370º=α, cosα =cos370º), но угол α не принадлежит промежутку [0; 180º], поэтому следует заменить 370º другим углом, косинус которого равен косинусу 370º, а и сам угол принадлежал бы промежутку

[0; 180º].

cos370º = cos (360º + 10º) = cos10º.

Таким образом, arccoscos 370º =10º- верный ответ.

 

в) аналогично предыдущему, аrсsinsin20 =20 – неверно найденное значение.

 

Следует обратить внимание, что число 20 – это не градусная мера угла (не 20º), а радианная (1 радиан = ).

sin 20= sin(20-2π∙3), (20-2π∙3) [0; π/2], поэтому аrсsinsin20=20-6π.

 

4. Ошибки, связанные с неправильным определением промежутка, содержащего заданный угол.

 

а) Определить знак числа sin4.

Ответ sin4>0 - неверный, так как 4 радиана –

это угол, принадлежащий третьей четверти (4≈57º∙4=228º), а в третьей четверти синус отрицательный, т.е. sin4<0.

 

б) Сравните значения выражений сos 34º и сos 330º.

Ответ сos34º >сos 330º - неверный, так как углы 34º и 330º не принадлежат одному промежутку монотонности функции y=cosx.. Заменим сos330º на равнное значение, сosα так, чтобы α

принадлежал одному промежутку монотонности с углом 34º. Используя свойство периодичности косинуса, получим: сos330º= сos(330º-360º) = cos30º.

Далее 30º<34º и оба этих угла принадлежат одному и тому же промежутку монотонности (в промежутке [0; 90º] косинус убывает), поэтому

cСos 34º< сos 30º, а, значит, и сos34º <сos 330º.

 

в) Сравните значения выражений sin4 и сos 3.

Ответ: sin4 >сos 3.

Проще сравнивать значения одноименных тригонометрических функций, поэтому заменим например, синус на косинус, по формулам приведения

sSin 4 = -сos(3/2π- 4), (3/2π- 4) [0; π/2]. сos 3 = - сos (π-3), (π- 3) [0; π/2].

Так как, 3/2π- 4 > π- 3 (перенесем в правую часть число 4, а в левую – π, получим π/2 > 1), то сos(3/2π- 4) < сos (π-3), а -сos(3/2π- 4) > -сos (π-3),

следовательно, sin4 > сos 3.

 

Для справки

1. a) Область определения (D) тригонометрических функций:

D(sin x) = (-∞; +∞); D(cosx) = (- ∞; +∞); D(tgx): х ≠ π/2 +πk, k – целое число.

 

b) Множество значений (E) тригонометрических функций:

E(sinx) = [-1; 1]; E(cosx) = [-1; 1]; E (tgx) = (-∞; +∞).

 

2.Период функций y =sinx и y =cosx равен 2π, период функции y=tgx равен π.

 

3.Функции y= sinx и y=tgx являются нечетными, функция cosx – четная:

sin(-x)=-sinx; tg(-x) = -tgx; cos(-x) =cosx.

 

4.Промежутки знакопостоянства и нули функции.

 

Промежутки знакопостоянства функции – числовые промежутки, на которых функция сохраняет свой знак (т.е. остается положительной или отрицательной). y

Промежутки знакопостоянства функции sinx: sinx

sinx > 0 х (2πk; π +2πк), k – любое целое

число;

sinx < 0 х (π +2πк; 2πk), k – любое целое х

число.

 

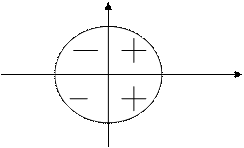Промежутки знакопостоянства функции cosx: y

сosx > 0 х (-π/2 +2πk; π/2 +2πк), k – любое cosx

целое число;

cosx < 0 х (π/2 +2πк; 3π/2+2πk), k – любое

целое число. х

y

Промежутки знакопостоянства функции tgx: tgx

tgx > 0

х (πk; π/2 +πк), k – любое целое число;

 

 

tg x < 0

х (-π/2 +πк; πk), k – любое целое число.

 

Нулями функции называются значения аргумента, при которых значение функции равно нулю.

Нули функции sinx: sinx=0, x= πк, k – любое целое число.

Нули функции cosx: cosx= 0, x = π/2 +πк, k – любое целое число.

Нули функции tgx: tgx =0, x= πк, k – любое целое число.

 

5. Функция f(x) называется возрастающей на множестве М, если для любых двух значений аргумента из множества М (х₁ и x₂), большему значению аргумента соответствует большее значение функции (если х₁>x₂, то

f(x₁)>f(x₂), а если х₁<x₂, то f(x₁)<f(x₂)).

 

 

Функция f(x) называется убывающей на множестве М, если для любых

двух значений аргумента из множества М (х₁ и x₂), большему значению аргумента соответствует меньшее значение функции (если х₁>x₂, то

f(x₁) <f(x₂), а если х₁<x₂, то f(x₁) >f(x₂)).

 

Функция, только возрастающая или только убывающая на множестве М, называется монотонной на этом множестве.

 

Функция y=sinx возрастает на промежутках (- π/2 +2πк; π/2+2πk), k – любое целое число.

Функция y=cosx возрастает на промежутках (- π+2πк; 2πk), k – любое целое число.

Функция y=sinx убывает на промежутках (π/2 +2πк; 3π/2+2πk), k – любое целое число.

Функция y=cosx убывает на промежутках (2πк; π+2πk), k – любое целое число.

Функция y=tgx возрастает на промежутках (- π/2 +πк; π/2+πk), k – любое целое число.

 

Раздел 2

 

Ошибки в тождественных преобразованиях

 

1.§1. Ошибки в действиях с многочленами

1.а) Большое число ошибок допускается при расскрытии скобок, если перед скобками стоит знак «минус».

Пример:

- (х - 2y +3) ≠ x + 2y - 3,

правильное решение: -(х - 2y + 3) = - x + 2y -3.;

 

б)2. При умножении многочлена на многочлен, если перед произведением стоит знак «минус» допускаются ошибки в знаках, если перед произведением стоит знак «минус».

.

Пример:

- (х-3)(2х-5) ≠ - 2х² - 6х - 5х +15,

правильное решение:

- (х-3)(2х-5) =-2х² + 6х + 5х -15 = -2х² + 11х -15.

 

в)3. Ошибки при разложении многочленов на множители.

Пример:

n⁶- n³+ n²+n+1=n³(n³-1)(n²+n+1)- это неверно,

так как при разложении на множители способом группировки,

· группы слагаемых заключаются в скобки ((n⁶- n³ )+ (n²+n+1)),

· затем из каждого многочлена в скобках выносится общий множитель (n³(n³-1)+(n²+n+1) = n³(n-1)(n²+n+1)+ +(n²+n+1)),

· затем вынеосится общий множитель (n²+n+1) полученных произведений.

Правильное решение: n⁶- n³+ n²+n+1 = (n⁶- n³ )+ (n²+n+1) =

= n³(n³-1)+(n²+n+1) = n³(n-1)(n²+n+1) +(n²+n+1) = (n²+n+1)(n³(n-1)+1) =

(n²+n+1)(n⁴ –n³+1).

 

4. г)Ошибки в разложении квадратного трехчлена на множители.

Пример:

2x² + 5x +3 = (x-1)(x-1,5)- это неверное решение.

Две типичные ошибки: нет числового множителя 2, неверно поставлены знаки в скобках.

Правильное решение: корни трехчлена -1 и -1,5.

 

2x² +5x+3 =2(x+1)(x+1,5) = (x+1)(2x+3).

 

5. д) Ошибки в применении формул сокращенного умножения.

 

Грубые ошибки:

a ² - b² ≠ (a- b)²,

a ² + b² ≠ (a-b)(a+b),

a³- b³ ≠ (a-b)(a²- ab+ b²),

a²+ab+ b² ≠ (a+ b)².

Для справки

Чтобы разложть квадратный трёхчлен на множители, надо:

1) найти корни х₁ и х₂ уравнения ах² + bх + с=0 (если корней нет,то квадратный трёхчлен разложить на множители нельзя);

2) разложить квадратный трёхчлен на множители по формуле:

ах² + bх + с = а (х – х₁) (х – х₂).

2.§2. Ошибки в действиях с алгебраическими дробями

1. а)Ошибки при сокращении дробей.

,

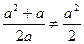такая ошибка - самая распространенная: «сокращение на слагаемое».

Правильное решение: .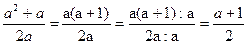

Для справки

Сократить алгебраическую дробь – это значит числитель и знаменатель дроби разделить на их общий множитель.

Чтобы сократить алгебраическую дробь (например, )

надо:

1) разложить числитель и знаменатель на множители:

числитель: а² - 36 = (а-6)(a+6);

знаменатель: 5а +30 = 5(а-6)

2) определить общий множитель: это (а+6);

3) разделить числитель и знаменатель на этот общий множитель:

иногда пишут:

(а-6) (а+6)

5(а+6)

 

б)2. Ошибки при сложении алгебраических дробей:

 

а) .

 

Распространеннная ошибка допущена при вычитании числителя второй дроби из числителя первой дроби.

Если перед дробью стоит знак «-», то следует поменять знак перед каждым слагаемым в числителе вычитаемого;

, правильно будет так: .

 

б) Другая распространенная ошибка - при отыскании общего знаменателя дробей:

.

Дополнительные множители для каждой дроби определены неправильно

(выбраны недостающие слагаемые, а нужны – недостающие множители).

Правильное решение:

 

 

 

Для справки

Приведение дробей к общему знаменателю.

Чтобы привести две алгебраические дроби к общему знаменателю надо:

1) разложить знаменатель каждой дроби на множители;

 

2) умножить числитель и знаменатель первой дроби на недостающие множители из разложения второго знаменателя;

 

3) умножить числитель и знаменатель второй дроби на недостающие множители из первого разложения.

 

 

в) Еще одна грубая ошибка:

Выполнено неверное сокращение дроби на x – y,

так как сокращать можно только на общий множитель числителя и знаменателя, а числитель не разложен на множители.

Следует разложить числитель дроби на множители, а затем выполнить сокращение, если это возможно.

Правильное решение:.

= .

 

г) Еще одна грубая ошибка. «Почленное деление»:

- это ошибочные преобразования.

 

На самом деле, почленное деление означает представление дроби в виде суммы дробей с тем же самым знаменателем, т.е. .

 

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: