 |
Применения обобщенных результатов к конкретному случаю, а также применения логических операций.
|
|
|
|
Анализ предложенных ответов и выбор правильного.
Проиллюстрируем сказанное на примерах.
1. Сокращение вычислительной части решения и громоздких
преобразований:
a) Вычислить катет треугольника, если его гипотенуза равна c =45, а другой катет – a =27. Вычисления выполнить без калькулятора.
Традиционно значение выражения вычисляется в указанном порядке действий b=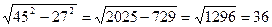 
;
проще: b =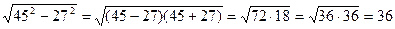 
.
б) Вычисление корней квадратного уравнения ax2 + bx + c = 0 с четным вторым коэффициентом по формуле: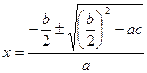 
сокращает вычисления.
Пример:
Решить уравнение 5x2 -28x + 32 = 0
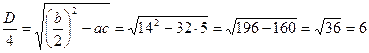
x1 =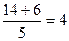 
; x2= 
.
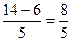в) Применение теоремы Виета для отыскания корней квадратного уравнения.
г) Применение теоремы Виета для решения систем вида 
д) Громоздкие преобразования получаются при вычислении площади треугольника по формуле Герона.
Например, если стороны треугольника имеют длины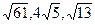 
, то его площадь равна
=
= 
= 
.
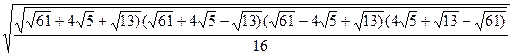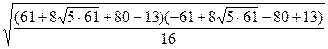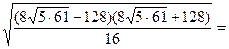
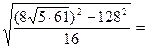
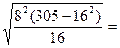
Задача упростится, если найти высоту треугольника. Заметим, что если BD высота треугольника ABC, то AB2-BC2 =AD2-CD2
или 61-13 = AD2 – (4 
-AD)2, 48 = AD2 - 80 + 8 AD - AD2, AD =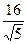 
.
Из треугольника ABD найдем высоту BD =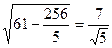 
.
Тогда площадь треугольника равна 
.
2. Применение свойств функций, множеств:
a) Решите уравнение
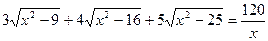
Решение
Поскольку левая часть уравнения неотрицательна, то и правая часть не меньше нуля, а с учетом области определения дроби и корня x ≥ 5.
При этих значениях x левая часть уравнения – функция возрастающая, а правая - убывающая, следовательно, данное уравнение может иметь не более одного корня. Подставим минимально возможное значение x =5, убедимся что уравнение обращается в верное числовое равенство. Значит, x = 5 – корень данного уравнения и других действительных корней нет.
|
|
|
Ответ: x =5
б) Для каждого значения a >1 решить неравенство:
ax (a-1)x -2ax+1 –(a-1)x +2a ≤ 0
Решение
ax (a-1)x -2ax+1 –(a-1)x +2a ≤ 0 
(ax -1) (a-1)x -2a(ax-1) ≤ 0
(ax -1) ((a-1)x -2a) ≤ 0 (a -1)x (a-2) (x- log a-12a) ≤ 0, a ≠ 2
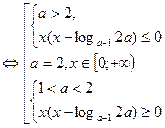
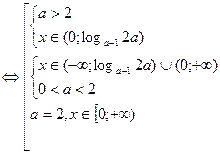
Ответ: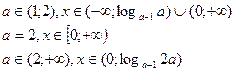 
Для справки
Знак выражения ax –at при a >1, a ≠ 1 совпадает со знаком выражения
(a-1)(x-t).
в) При каких натуральных значениях n число m = 
является целым числом?
Приводится решение:
m =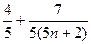 
. Умножим обе части равенства на 5, получим: 5m = 
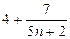. Теперь, очевидно, что решения задачи будут среди тех натуральных n, при которых число 5n + 2 является делителем числа 7. Т.е. n = 1. При этом n целым будет число 5m.
Проверим, будет ли целым число m. При n = 1: m = =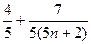 
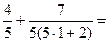1. Значит, n =1 удовлетворяет требованию задачи.
Ответ: n=1
Рациональное решение
Необходимым условием того, чтобы при натуральных n число было целым является 4n+3 ≥5 n+2.
Откуда: n ≤ 1. Остается только убедиться, что при при n =1 число -
целое.
3. Графическое представление математических объектов:
а) Решите уравнение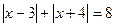 
.
Решение 1
Решим это уравнение методом интервалов:
a) при x <-4: -x + 3 - x- 4 = 8: x = -4,5 
(-∞; -4), -4,5- корень уравнения.
б) при x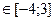 
: -x + 3 + x+4 = 8. 7=8. Так как полученное равенство является
неверным, то на данном отрезке уравнение решений не имеет.
в) при x >3: x - 3 + x + 4 = 8: x =3,5 (3;+ ∞), т.е. 3,5- корень уравнения
Ответ: -4,5;3,3.
Решение 2
График функции h(x) =│x-3│+│x+4│ представляет собой объединение двух лучей и отрезка, параллельного оси OX. Ординаты точек отрезка равны
│-3-4│=7.
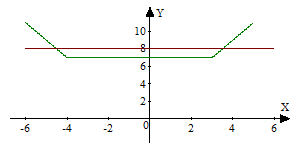
Следовательно, прямая y = 8 пересекает график функции h(x) в двух точках – точках пересечения с лучами. Значит, данное уравнение имеет два решения: x-3+x+4 = 8, x =3,5; -x+3-x-4 = 8, x =- 4,5;
Ответ: -4,5;3,3.
Для справки
График уравнения h(x) =│x-a│+│x-b│, a>b.
1. при x=a h(x) =│b-a│;
2. при x=b h(x) =│b-a│;
|
|
|
3. при x > a, x = a+1 h(x) =│a+1-a│+│a+1-b│= 1+│a+1-b│;
4. при x <b, x = b-1 h(x) =│b-1-a│+│a+1-a│= 1+│a+1-b│;
5. при x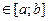 
- отрезок, параллельный оси oX, проходящий через точку
(0;│b-a│).
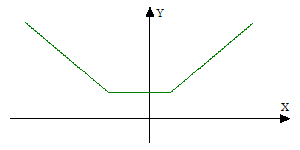
С помощью графических представлений решается уравнение
│x-a│+│x-b│= с.
1. Если с =│b-a│, то решение – отрезок [a;b]
2. Если с < │b-a│, то уравнение решений не имеет.
3. Если с >│b-a│, уравнение имеет два корня.
б) При каких a уравненние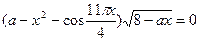 
имеет на [-2;3] нечетное число решений?
Решение
Произведение двух множителей равно нулю, если один из них равен нулю, а другой при этом не теряет смысл. Поэтому данное уравнение на [-2;3] равносильно совокупности двух систем:
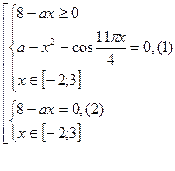
Замечаем, что функция f(x) = a –x2 –cos11π/4x четная и поэтому уравнение (1) на симметричном множестве [-2;2] может иметь нечетное число решений только, если x=0 – корень уравнения (1). Найдем значения a, при которых x = 0 – корень этого уравнения.
a - 0 + cos0 =0, откуда a = 1.
При a = 1 уравнение 1 имеет вид: cos11π/4x = –x2 +1и на [-2;2] имеет нечетное число решений. Проверим, сколько решений имеет уравнение (1) на [2;3].
Так как (– x2 +1) 
[-1;1] для x [2;3], то на [2;3] уравнение (1) решений не имеет.
Условие 8 –ax ≥ 0 для a = 1 и x [-2;2] выполняется.
Уравнение (2) при a = 1 имеет вид 8 – x = 0 и на [-2;3] решений не имеет.
Таким образом, при a = 1 данное уравнение имеет на [-2;3] нечетное число решений.
При a ≠1 уравненние (1) на симметричном множестве [-2;2], если и имеет, то четное число корней, а уравнение (2) имеет один корень, если a ≠0.
Если a = 0, то уравнение (2) не имеет корней, а уравнение (1) имеет вид
cos11π/4x = –x2 и на [-2;2] может иметь лишь четное число корней, а на [2;3] решений не имеет, так как (– x2 +1) [-1;1], для x [2;3].
Таким образом, при a = 0 данное уравнение не имеет на [-2;3] нечетного числа решений.
Если a ≠0, то уравнение (2) имеет единственный корень x = 8/a.Найдем значения a, при которых этот корень попадает в промежуток [-2;3], т.е. решим неравенство
-2 ≤ 8/a ≤ 3. Получим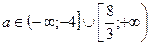 
.
Исследуем, сколько корней, удовлетворяющих условию задачи, для 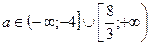имеет данное уравнение, при этом будем следить за возможными совпадениями корней уравнений (1) и (2).
Представим уравнение (1) в виде cos11π/4x = a – x2.
Построим график функции g(x)= cos11π/4x на [0;3]. T= 8/11. (рис.1).
|
|
|
График функции h(x) = a – x2 если пересекает график функции на [-2;2], то в симметричных точках относительно начала координат, поэтому будем рассматривать этот график только на [0;3]
Будем наблюдать за абсциссами точек пересечения этих графиков при различных значениях a.
Если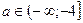 
, то точек пересечения нет, значит при этих a уравнение (1) не имеет решений, а данное уравнение имеет только одно решение.
Если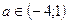 
, то графики функций g и h либо не пересекаются, либо имеют четное число точек пересечения на [-2;3], значит данное уравнение не имеет на [-2;3] нечетного числа решений.
Если a = 1, то как уже отмечалось, данное уравнение имеет нечетное число решений на [-2;3]. Это можно увидеть и на графиках.
Если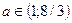 
, то графики функций g и h пересекаются только на [-2;2], а значит уравнение (1) имеет четное число решений, а данное уравнение не имеет на [-2;3] нечетного числа решений.
Если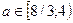 
, то графики функций g и h пересекаются только на [-2;2], а значит уравнение (1) имеет четное число решений на [-2;3]. Тогда данное уравнение имеет на [-2;3] нечетное число решений.
Если a = 4, то графики функций g и h пересекаются в точках 2 и -2 на оси абсцисс, а значит уравнения (1) и (2) имеют совпадающий корень x = 2, и если уравнение (1) имеет корни на [2;3], то они не удовлетворяют условию
8-ax ≥ 0
Таким образом, при a = 4 данное уравнение не имеет на [-2;3] нечетного числа решений.
Если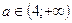 
, то уравнение (1) если имеет, на [-2;2] корни, то их четное число, а если есть решения на [2;3], то они не удовлетворяют условию
8-ax ≥ 0.
Таким образом, при 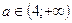данное уравнение имеет на [-2;3] нечетное число решений.
Ответ: (-∞;-4]U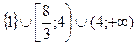 
.
4. Интеграция методов различных разделов алгебры и геометрии при
решени задач:
а) Решите в действительных числах уравнение:
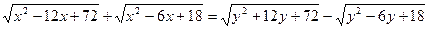
Решение
Запишем данное неравенство в виде:
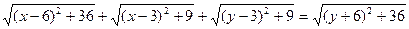
Левую часть равенства можно рассматривать как сумму длин звеньев ломанной с вершинами в точках A(-6;6), B(x;0), C(3;3), D(0;y), а правую -
как отрезок, соединяющий начало и конец этой ломанной.
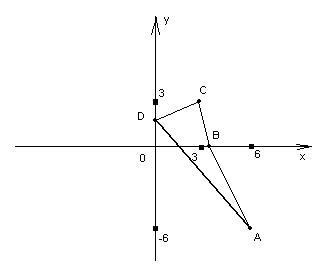
По свойству ломанной ее длина больше отрезка, соединяющего ее концы. Равенство возможно, если все точки A(6;-6), B(x;0), C(3;3), D(0;y) лежат на одной прямой. Точки A(6;-6) и C(3;3) определяют эту прямую. Запишем уравнение прямой, проходящей через эти две точки: y = -3x +12.
|
|
|
Точки B(x;0), D(0;y) – это точки пресечения найденной прямой с кординатными осями. Тогда x = 4,y = 12.
Ответ: x = 4,y = 12.
б) Найдите угол наклона касательной, проведенной из точки (1,5;0,5) к графику функции y =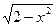 
.
Приводится решение
Так как точка A (1,5;0,5) не принадлежит графику функции, то для определения угла наклона касательной нужно определить абсциссу точки касания прямой с графиком функции. Обозначим эту точку M (x0;y0). Запишем уравнение касательной к графику функции y = f(x). в точке (x0;y0):
y = f’(x0)x - f’(x0)x0 +f(x0). Если f(x) = 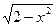, то f’(x0) = 
и уравнение касательной будет иметь вид y = x - x0 +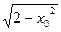 
.
Поскольку точка A(1,5;0,5) принадлежит касательной, то ее координаты удовлетворяют последнему уравнеию. Подставим координаты этой точки в уравнение, получим уравнение относительно x0:
0,5= 1,5- x0 + .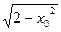
Решая это уравнение, получаем единственный корень x0 =1.
Найдем значение производной в этой точке
f’(x0) = -1- это тангенс угла наклона касательной к оси OX, угол будет равен 135о.
Ответ 135о.
Рациональное решение:
Построим график функции y = 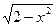, это полуокружность с центром в начале координат и радиусом, равным 
(у = ,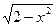 
).
Проведем касательную к окружности из точки A (1,5;0,5), см. рис.
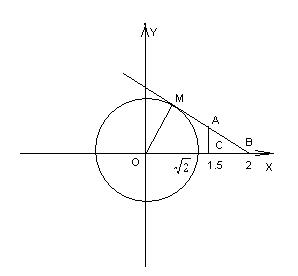
Треугольники OMB и ACB подобны. Тогда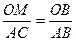 
или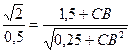 
.
Решая это уравнение, получаем CB = 1. Тогда OB = 2 и из прямоугльного треугольника OMB находим, что угол OBM равен 45˚, а смежный с ним угол между касательной и осью OX равен 135˚.
Ответ 135о.
в) Решите неравенство
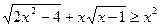
Решение
Заметим, что x = 2 – решение данного неравенства. Заменим левую часть неравенства на большее выражения при x > 2. По неравенству между средним арифметическим и средним квадратичным будем иметь:
.
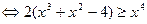
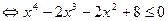
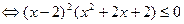Последнее неравенство
справедливо только при x = 2, поскольку это неравенство является следствием данного, то данное неравенство других решений не имеет.
Ответ: x = 2
5. Применения обобщенных результатов к конкретному случаю, а также применения логических операций:
а) Сравните log34 и log56
Приводится решение
Сравним log34 с числом 5/4. 5/4 = log3 35/4 =
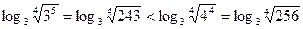, т.е. log34 > 5/4.
Сравним log5 6 с числом 5/4. 5/4 = log5 55/4 =
, т.е. log56 < 5/4.
Таким образом, log34 > log56.
Рациональное решение
Рассмотрим функцию f(x) =logx (x+1). Нужно сравнить f(5) и f(3). Исследуем эту функцию на монотонность:
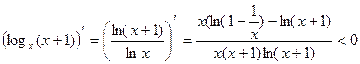для x >1, значит для натуральных n эта функция монотонно убывает, т.е. f(5) <f(3).
Таким образом, log34 > log56.
б) При каких значениях параметра a система
|
|
|
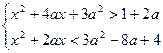(1) имеет хотя бы одно решение?
Решение 1
Рассмотрим квадратные трехчлены f(x) = x2 + 4ax +3a2 -1-2a (1) и
g(x) = x2 +2ax - 3a2 +8a -4 (2).
Корни первого трехчлена x1= -3a -1, x2=-1+a.
Тогда решение первого неравенства системы будет объединение двух промежутков (-∞;-3a-1) и (-a +1; +∞) при условии -3a-1 ≤ -a +1, или (-∞;-a+1) и (-3a -1;+∞) при условии -3a-1 ≥-a +1.
У второго трехчлена корни так же существуют: x3 = -3a+2 и
x4 = a-2. Поэтому решение второго неравенства - интервал (-3a+2;a-2) при условии -3a+2 ≤ a -2 или (a-2;-3a+2) при условии -3a+2 ≥a -2.
Для того, чтобы система имела хотя бы одно решение достаточно, чтобы объединение двух промежутков и интервал имели общие точки. Рассматрим все возможные случаи:
1. 
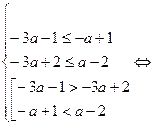
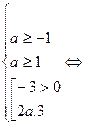
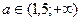
2. 
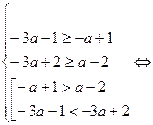
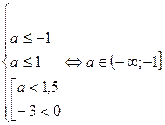
3. 
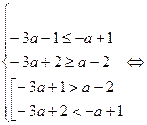
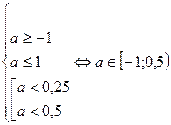
Объединяя все найденные промежутки, получим ответ a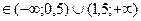 
.
Ответ: a .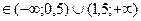
Решение 2
Рассмотрим противоположную задачу: при каких значениях параметра a
система (1) не имеет решений? Это значит, что корни второго трехчлена дожны находиться между корнями первого или совпадать с ними. Для этого достаточно, чтобы выполнялось условие (см. рис.)
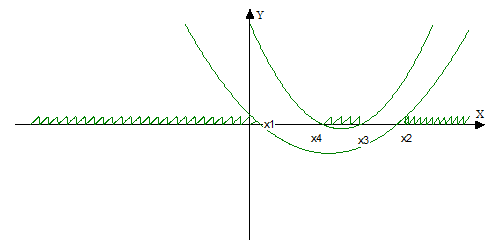
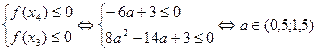
Тогда система (1) будет иметь хотя бы одно решение при
a .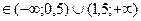
Ответ: a .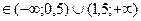
|
|
|
