 |
2.Температура поверхности постоянна, но в начальный момент времени имеется распределение температур по сечению тела соответствующее параболе 2го порядка.
|
|
|
|
2. Температура поверхности постоянна, но в начальный момент времени имеется распределение температур по сечению тела соответствующее параболе 2го порядка.
Граничные условия соответствуют граничным условиям, приведённым в 1м варианте
t /x ± S = tп; t / r = R =tп; tп = const
Начальные условия для пластины
|
tc - температура середины тела в начальный момент времени;
Dtн = tп - tс - перепад температур между поверхностью и серединой тела;
tп - температура поверхности тела.
Таким образом, на поверхности тела температура одинакова и равна tп как в начальный момент времени, так и в течение всего рассматриваемого промежутка времени.
Подставив граничные и начальные условия в общее решение уравнения теплопроводности для граничных условий 1го рода, после интегрирования и преобразования получим решение для пластины
t = tп + ( tс - tп )× (20)
или в критериальной форме
| |||
 | |||
|
|
|
|
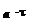Значения Ф1 вычислены и представлены в виде графиков.
Для цилиндра аналитическое решение при заданных граничных условиях выглядит так
t = tп + ( tс - tп )× (21)
i0 и I1 - функции Бесселя нулевого и 1го порядка.
mn - значение корней характеристического уравнения
Решение в критериальной форме будет иметь вид
qц = F1( Fo; r / R ),
Выведенные решения могут применяться для определения температурного поля в пластине и цилиндре во время выдержки в печах. Эти же формулы могут служить для решения обратной задачи - определения продолжительности выдержки.
Для бесконечной пластины температура в середине тела в момент времени t может быть найдена по формуле ( при а× t / S2 ³ 0, 06 )
|
|
|
|
|
Для цилиндра бесконечной длины т емпература на оси может быть рассчитана по формуле ( при а× t / R2 ³ 0, 08 )
|
|
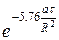
Для цилиндра радиусом R и высотой 2Н
|
|
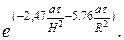
37. Температура печи и тепловой поток во время выдержки
Для определения необходимой температуры печи во время выдержки воспользуемся выражением, связывающим закон теплопроводности и закон теплоотдачи от газов к поверхности металла
|
|
|
|
|
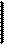
Определив ¶t / ¶х из решения (20) при х = S и подставив в выражение (22) получаем для пластины
t печ = tпов + (tпов - tc)× ; (23)
или в общем виде
|
|
Аналогично для цилиндра
|
|
Значения F приведены в литературе.
Тепловой потокопределяется из выражения (23).
Для пластины
q = a( tпеч - tпов ) = (tпов - tc). (24)
Или 
(25)
Для цилиндра
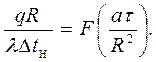(26)
Значения F приведены в литературе.
Известно, что теплообмен излучением в рабочем пространстве печей может быть выражен в форме
q = Cпр× 
где СПР - приведённый коэффициент излучения.
Отсюда
tПЕЧ = 100× 
где q для пластины и цилиндра определяются из выражений (24), (25), (26).
38. Нагрев с постоянной скоростью изменения температуры поверхности
Тогда граничные условия.
Для пластины бесконечной длины и ширины t x = ± S = tн +C× t
Для бесконечного цилиндра t r = R = tн + C× t.
|
|
|
Начальные условия.
Температурный градиент в начальный момент времени отсутствует.
t t = 0 = tн= F (x)
t t = 0 = tн = F (r)
tн - начальная температура поверхности тела, 0С.
С- скорость нагрева (изменение tпов тела), 0С / ч
Подставляя граничные и начальные условия в общее уравнение теплопроводности при граничных условиях 1го рода, получим
Для пластины
t = tн + C× t + 
Для цилиндра
t = tн + C× t + 
Результаты расчёта функции Ф приведены литературе в виде графиков.
При t > S2/ а - для пластины и t > 0, 5× R2/ а - для цилиндра функция Ф принимает столь малые значения, что они могут быть отброшены.
Тогда решения принимают вид
Для пластины
t = tн + C× t + 
Для цилиндра
t = tн + C× t + 
Для середины пластины, цилиндра, т. е. при х / S = 0; r / R = 0
tc = tн + C× t -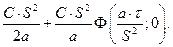 
tc = tн + C× t - 
При t > S2/ а - для пластины и t > 0, 5× R2/ а - для цилиндра решения принимают вид
tc = tн + C× t - 
tc = tн + C× t -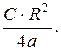 
|
|
|
