Геометрические принципы позиционирования

И системы координат

Общие сведения. Любая точка в пространстве характеризуется, как известно, тремя координатами, которые могут быть линейными, угловыми или смешанными. Существует несколько различных систем пространственных координат, подробно изучаемых в курсе высшей геодезии. В спутниковой геодезии наиболее удобной является геоцентрическая (т.е. с началом в центре масс Земли) прямоугольная система координат Х,Y,Z. Связь между этой системой и широко применяемой в высшей геодезии системой геодезических (пространственных эллипсоидальных) координат B,L,H (геодезических широты, долготы и высоты) устанавливается известными формулами. Нас будет здесь интересовать несколько иной аспект. В какой бы системе координат ни рассматривалась данная (определяемая) точка пространства, прежде всего надо определить ее местоположение по отношению к другим точкам, координаты которых известны, при помощи измерений некоторых геометрических величин, линейных или угловых. Поскольку электронными методами расстояния измеряются точнее, чем углы, то естественно выбрать в качестве измеряемых линейные, а не угловые величины. Тогда пространственное положение точки можно получить методом линейной засечки. Поясним сказанное, рассмотрев сначала для простоты ситуацию на плоскости. Пусть (рис.2.1,а) А и В - точки с известными координатами (как принято говорить в геодезии, “твердые” пункты), Р - определяемая точка. Для нахождения ее местоположения на плоскости надо измерить расстояния от нее до точек А и В, т.е. АР и ВР. Тогда точка Р получается в пересечении двух окружностей с радиусами АР и ВР. (Эти окружности пересекаются в двух точках - вторая точка лежит на рисунке снизу от линии АВ, - но на практике мы всегда можем правильно выбрать нужную точку). Окружности представляют собой изолинии (так называются линии равных значений измеренных величин) - линии равных расстояний от центра окружности. Следовательно, в этом случае измерение двух расстояний от твердых точек до определяемой дает положение последней в пересечении двух круговых изолиний. При этом точность засечки тем выше, чем ближе к 90^о угол засечки g. Поскольку измеряются расстояния (дальности), такой метод определения местоположения называется дальномерным.

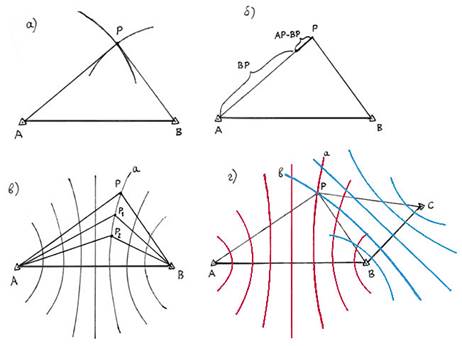
Рис. 2.1. К определению местоположения точки на плоскости круговой и гиперболической засечкой

Рассмотрим еще один пример на плоскости. Предположим (рис.2.1,б), что мы получили из измерений не сами расстояния АР и ВР, а их разность АР-ВР. Из аналитической геометрии известно, что разность расстояний - это параметр гиперболы. По определению, гипербола - это геометрическое место точек, для каждой из которых разность расстояний до двух заданных точек, называемых фокусами, есть величина постоянная. Значит, если на линии АВ построить семейство гипербол с фокусами в А и В (рис.2.1,в), то разность расстояний АР-ВР = а будет определять гиперболу, проходящую через точку Р, но положение точки Р на этой гиперболе еще не определено - разность расстояний до А и В будет одинаковой и равной а для любой точки гиперболы - например, Р₁, Р₂ и т.д. Другими словами, эта гипербола есть изолиния - линия равных разностей расстояний, на которой лежит определяемая точка Р. Чтобы ее засечь, надо иметь еще одну твердую точку С и измерить разность расстояний ВР-СР = b (рис.2.1,г). Это даст еще одну гиперболу, проходящую через точку Р, из второго семейства гипербол, построенных на базисе ВС с фокусами в точках В и С, т.е. вторую изолинию. Тогда положение точки Р будет зафиксировано в пересечении двух гиперболических изолиний. Величины а и b - разности расстояний - часто называют гиперболическими координатами точки Р. Поскольку измеряются разности расстояний, такой метод местоопределения называется разностно-дальномерным или просто разностным.

При переходе от плоскости к пространству изолинии заменяются изоповерхностями, и их должно быть уже не две, а три, т.е. число измеряемых геометрических параметров - расстояний или разностей расстояний - должно быть равно трем. При дальномерном методе вместо окружностей получаем сферы, и определяемая в пространстве точка получается в пересечении трех сферических поверхностей. Пересечение двух сфер дает окружность, а третья сферическая поверхность пересекает эту окружность в двух точках, одна из которой и является определяемой. По трем измеренным дальностям D _i (i = 1,2,3) координаты определяемой точки X,Y,Z вычисляются из решения трех уравнений (уравнений сферы) вида:

D _i = [(X - X _i)² + (Y - Y _i)² + (Z - Z _i)²]^1/2, (2.1)

где X _i, Y _i, Z _i - известные координаты точек, от которых измерялись расстояния (центров сфер).

При разностно-дальномерном методе определяемая точка получается аналогичным образом как одна из двух точек в пересечении трех гиперболоидов, образованных вращением гипербол вокруг базовых линий; при этом для получения трех разностей расстояний необходимо иметь четыре твердых пункта.

Сказанное справедливо как для неподвижной, так и для движущейся определяемой точки. В последнем случае требуется лишь соблюдение условия одновременности измерений трех расстояний или трех разностей расстояний от определяемой точки до пунктов с известными координатами.

Особенности спутникового позиционирования. При применении вышеизложенных геометрических принципов определения местоположения к глобальным спутниковым системам возникают некоторые специфические особенности. Одна из них заключается в том, что “твердыми пунктами” - точками с известными координатами - являются движущиеся спутники, а определяемая точка (неподвижная или движущаяся) находится на Земле (спутниковый приемник). Для определения положения (координат) этой точки выполняется одновременное измерение дальностей (расстояний) до спутников, а положение точки геометрически получается в пересечении сфер, как было пояснено выше, т.е. используется дальномерный метод. Другая особенность состоит в том, что по причинам, которые будут рассмотрены в следующем разделе, измеряемые дальности получаются искаженными. Их называют псевдодальностями. Чтобы правильно вычислить координаты приемника по измеренным псевдодальностям, их надо измерять не до трех спутников, а как минимум до четырех. На практике, как правило, используется большее количество спутников для получения избыточных измерений, позволяющих повысить качество окончательного результата и оценить его точность, но с принципиальной точки зрения достаточно четырех спутников.

Еще одной особенностью является то, что, наряду с дальномерным методом, в глобальных спутниковых системах используется (как вспомогательный, для грубой оценки местоположения) и разностный метод (который был основным в низкоорбитальных спутниковых системах первого поколения). При этом возможны два варианта. Первый из них состоит в измерении разностей расстояний между наземным приемником и двумя положениями S₁ и S₂, S₂ и S₃, S₃ и S₄ одного и того же спутника в последовательные моменты времени (как это делалось в системах первого поколения). Второй вариант возможен при наличии в поле зрения достаточного количества спутников для того, чтобы производить одновременные наблюдения трех пар спутников, получая для каждой пары разность расстояний. Оба варианта основаны на использовании эффекта Допплера, который позволяет также получить радиальную скорость - скорость изменения расстояния между спутником и приемником. Каким образом допплеровские измерения связаны с разностями расстояний и скоростью, рассмотрено в разделе “Интегральный допплеровский счет”.

Системы координат при спутниковом позиционировании. Выше указывалось, что спутники являются объектами с известными координатами. Конкретная точка, к которой относятся координаты - это так называемый фазовый центр передающей антенны на спутнике. Откуда берутся эти координаты и что они собой представляют?

В состав спутниковой системы входит сеть наземных станций слежения, которые в результате измерения расстояний до спутника получают данные об элементах орбиты спутника через равноотстоящие интервалы времени в пределах некоторого участка траектории движения. Обработка этих данных, называемых эфемеридной информацией или просто эфемеридами спутника, позволяет вычислить для ряда моментов времени координаты фазового центра антенны спутника в геоцентрической прямоугольной системе координат. Напомним, что эта система определяется следующим образом (рис.2.2):

начало координат О расположено в центре масс Земли;

ось Z направлена вдоль оси вращения Земли в точку среднего положения Северного полюса на эпоху 1900 -1905 гг. (Международное условное начало);

ось Х лежит в плоскости земного экватора и направлена в точку пересечения этой плоскости с Гринвичским меридианом G;

ось Y дополняет систему до правой.

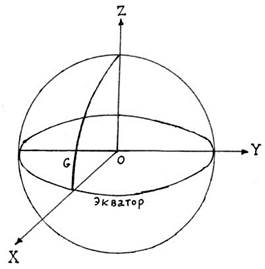
Рис.2.2. Геоцентрическая прямоугольная система координат

GPS действует в геоцентрической системе координат, называемой WGS-84 (World Geodetic System, 1984), а ГЛОНАСС - в геоцентрической системе ПЗ-90 (Параметры Земли, 1990). Эти системы координат близки друг к другу. Их различие можно свести к небольшому повороту системы относительно оси Z и смещению начала координат по этой оси на величину около 4 м (рис.2.3).

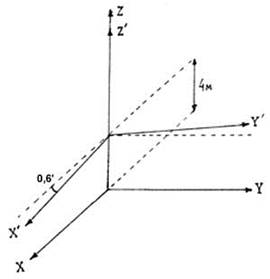
Рис.2.3. Системы координат WGS-84 и ПЗ-90

Следует отметить, что аббревиатурами WGS-84 и ПЗ-90 обозначают не только системы координат, но и общие земные эллипсоиды, три взаимно-перпендикулярные оси которых направлены по соответствующим координатным осям (X,Y,Z для WGS-84 и X',Y' Z'=Z для ПЗ-90).