Зоны радиовидимости. Режимы работы.

Системы GPS и ГЛОНАСС состоят из трех секторов (в зарубежной литературе их именуют сегментами, а в отечественной часто называют подсистемами). Это:

1. космический сектор,

2. наземный сектор управления и контроля

3. сектор пользователя (рис.4.1).

Рис.4.1. Общая структура глобальных спутниковых систем

Космический сектор - это совокупность входящих в систему спутников, часто называемая "созвездием" или "орбитальной группировкой". На каждом спутнике установлены атомные эталоны частоты и аппаратура, передающая необходимые для измерений радиосигналы, в состав которых входит так называемое навигационное сообщение, содержащее сведения о положении спутников, метки времени, различные поправки и другую необходимую информацию. Кроме передающей аппаратуры, спутник содержит и радиоприемное устройство для приема команд и сигналов от наземного комплекса управления и контроля. Каждый спутник снабжен панелями солнечных батарей питания, двигательной установкой для коррекции траектории движения спутника по командам с Земли и системами ориентации и стабилизации.

Как в GPS, так и в ГЛОНАСС полное созвездие состоит из 24 спутников. В GPS они расположены в шести орбитальных плоскостях, развернутых через 60°, а в ГЛОНАСС - в трех плоскостях через 120°. Орбиты спутников весьма близки к круговым. В таблице 4.1 указаны некоторые основные параметры орбитальных группировок для обеих систем.

Таблица 4.1

Параметр	GPS	ГЛОНАСС
Число спутников в системе Число орбитальных плоскостей Наклон орбиты к плоскости экватора Высота орбит Период обращения спутников	24 6 55о 20145 км 11 час 57 мин	24 3 64,8о 19100 км 11 час 16 мин

Сектор управления и контроля. Включает в себя станции слежения, службу точного времени, главную станцию с вычислительным центром и станции загрузки информации на спутники. В GPS пять станций слежения распределены равномерно но земному шару; одна из них совмещена с центральной управляющей станцией в Колорадо-Спрингс (США). Полученная на этих станциях информация об элементах орбит и прогнозируемых координатах спутников передается при помощи трех загружающих станций на спутники. Существует также не входящая в систему управления и контроля, но более глобальная и точная сеть следящих станций - Объединенная международная сеть GPS под названием CIGNET (Cooperative International GPS Network), находящаяся в ведении Национальной геодезической службы (NGS) США. В ГЛОНАСС сеть станций слежения расположена на территории бывшего СССР. Станции оборудованы радиолокаторами и лазерными дальномерами, а спутники - отражателями. Под Москвой расположен Центр управления системой (ЦУС), включающий и себя центральный синхронизатор (ЦС) с водородным стандартом частоты.

Сектор пользователя включает в себя спутниковые приемники, число которых не ограничено, а также камеральный комплекс обработки измерений (“постобработки”, выполняемой после полевых наблюдений).

Зоны радиовидимости. Для надежного выполнения измерений на трассе “спутник - приемник” необходимо, чтобы эта трасса находилась в зоне, в пределах которой обеспечивается взаимная прямая видимость между спутником и приемником. На рис.4.2 а, б показаны зоны радиовидимостис наземного пункта и со спутника соответственно (заштрихованные участки).

Рис. 4.2. Зоны радиовидимости с наземной станции (а) и со спутника (б)

Рассмотрим подробнее рис.4.2,а. На нем t₁ - момент входа, t₂ - момент выхода спутника из зоны радиовидимости, определяемой геоцентрическим углом 2b. Из треугольника t₁Ot₂, пользуясь теоремой синусов, нетрудно установить, что угол b определяется соотношением:

b = arccos () - d, (4.1)

где R - радиус Земли, Н - высота орбиты спутника. Такое же соотношение получается и для рис.4.2,б.

Определим размеры зоны радиовидимости спутника на поверхности Земли. Она будет определяться длиной дуги S = AB на рисунках 4.2 а,б. Длина дуги в радианах равна: S = 2Rb, или, подставляя выражение (4.1) для b,

S = 2R [ arccos () - d ]. (4.2)

Это будет сферический диаметр зоны радиовидимости. Угол d определяет минимальную высоту спутника над горизонтом, при которой возможен надежный прием радиосигналов. Этот угол называется маской и обычно составляет не менее 10^о. Полагая d = 10^о, R = 6371 км и Н = 20 000 км, получим S = 14 700 км.

Поскольку спутник движется, будет непрерывно перемещаться и зона его радиовидимости, образуя на земной поверхности полосу радиовидимости, как схематически показано на рис.4.3.

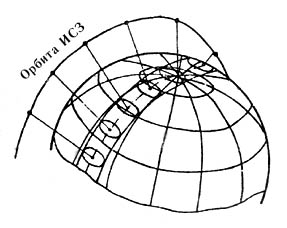
Рис.4.3. Образование полосы радиовидимости при движении спутника по орбите

Режимы работы систем. Глобальные спутниковые системы могут работать в двух основных режимах, получивших название кодовых измерений и фазовых измерений. При кодовых измерениях выполняется измерение времени распространения кодово-модулированного сигнала от спутника до приемника, а при фазовых - измерение сдвига фазы колебания несущей частоты за время распространения. Следует отметить, что для этих режимов часто используют иные названия, характеризующие их, так сказать, с другой стороны. Режим кодовых измерений называют навигационным, а также абсолютными определениями, а режим фазовых измерений - геодезическим, а также относительными определениями. Такая терминология используется потому, что кодовые измерения дают меньшую точность, приемлемую при решении задач навигации, и при этом обеспечивают непосредственное получение самих координат (абсолютных величин). Фазовые же измерения дают высокую точность, пригодную для геодезических целей, но при этом позволяют получить не сами координаты, а разности одноименных координат двух (или более) точек, в которых установлены одновременно работающие приемники.

Иногда в отдельный (третий) режим выделяют так называемый интегральный допплеровский счет, который осуществляется, по сути дела, одновременно с режимом фазовых измерений. Он позволяет получать скорость изменения расстояния до спутника и фиксировать моменты последовательных положений спутника.

Все три указанных режима будут подробно рассмотрены в последующих разделах.

Спутниковый сигнал

Структура сигнала. Передаваемый со спутника сигнал представляет собой излучаемые в пространство электромагнитные колебания на двух несущих частотах, обозначаемых L1 и L2, подвергнутых особому виду фазовой модуляции - фазовой манипуляции. Последняя состоит в переброске фазы несущей на 180^о в определенные моменты. Эти моменты задаются так называемыми дальномерными кодами - определенными последовательностями нулей и единиц. Переброска фазы происходит в моменты смены в кодах 0 на 1 или 1 на 0 (рис.5.1).

Рис.5.1. Фазовая манипуляция под действием кодового сигнала

Таких кодов используется два: один для "грубых", другой для "точных" измерений, и они существенно различаются, о чем будет подробнее сказано ниже. Грубым кодом модулируется несущая L1, а точным кодом - обе несущих L1 и L2. В GPS грубый код называется С/А-кодом (от слов Coarse Aquisition - легко обнаруживаемый, общедоступный), а точный – Р-кодом (Precision - точный). С/А-код предназначен для всех пользователей. Р-код изначально предназначался только для имеющих санкционированный доступ (в основном для американских военных).Сейчас, однако, доступ к Р-коду имеют приемники практически всех пользователей. В системе ГЛОНАСС аналогичная ситуация, разница только в названиях: грубый код называется СТ-кодом (кодом стандартной точности), а точный код - ВТ-кодом (кодом высокой точности). Однако между GPS и ГЛОНАСС есть принципиальное различие, относящееся к использованию кодов. В GPS как С/А-код, так и Р-код различны для каждого спутника при одинаковости несущих частот L1 и L2 для всех спутников системы. В ГЛОНАСС же, наоборот, коды СТ и ВТ всех спутников одинаковы, но различны несущие частоты. Другими словами, в GPS применено кодовое, а в ГЛОНАСС - частотное разделение сигналов от каждого спутника.

Применение кодов решает задачу измерения расстояний (псевдодальностей) временным методом с использованием корреляционной обработки сигнала. Как это делается, будет рассмотрено в разделе "Кодовые измерения".

Но спутниковый сигнал подвержен не только кодовой модуляции, необходимой для измерения расстояний. В него "встраивается" вся передаваемая со спутника информация - метки времени, данные об эфемеридах спутника, различные поправочные величины, альманах (сборник менее точных данных о местонахождении каждого из спутников системы и состоянии его “здоровья”) и др. Вся эта информация, образующая навигационное сообщение, также преобразуется в двоичный код (последовательность нулей и единиц), которым дополнительно модулируются обе несущих частоты. Модуляция осуществляется так же, как и дальномерными кодами - переброской фазы несущего колебания на 180° в моменты смены символов (нулей и единиц). Частота следования символов навигационного сообщения составляет 50 Гц (или, как говорят, информация передается со скоростью 50 бит/с, так как один символ - 0 или 1 - содержит один бит информации).

Таким образом, сигнал каждого спутника в обеих рассматриваемых глобальных системах состоит из двух несущих колебаний различных частот, манипулированных по фазе как дальномерными кодами, так и навигационным сообщением. Дальнейшее более детальное рассмотрение этого вопроса будет ориентировано в основном на систему GPS как на получившую более широкое применение, в том числе и у российских пользователей.

На рис.5.2 показан принцип формирования спутникового сигнала в GPS. Высокостабильный опорный кварцевый генератор, стабилизированный при помощи атомных эталонов частоты, генерирует колебания с частотой 10,23 Мгц, из которых соответствующим умножением или делением (это показано на рисунке) синтезируются все остальные частоты - несущие, частоты следования символов С/А- и Р- кодов (тактовые частоты) и символов навигационного сообщения.

Рис.5.2. Схема формирования спутникового сигнала в GPS

В таблице 5.1 указаны номиналы всех частот и способ их получения.

Таблица 5.1

Элементы сигнала	Частота	Способ получения
Несущая L1 Несущая L2 C/A-код P-код Навигационное сообщение	1575,42 МГц 1227,60 МГц 1,023 МГц 10,23 МГц 50 Гц	10,23 МГц ´ 154 10,23 МГц ´ 120 10,23 МГц: 10 10,23 МГц без измен. 10,23 МГц:204600

Сигналы С/А-кода и Р-кода суммируются с сигналами навигационного сообщения и поступают в фазовые манипуляторы, в которых под действием этих сигналов осуществляется переворот фазы несущих колебаний L1 и L2 на 180^о. При этом, как видно из рис.5.1, канал несущей L1 разделен на две части, в одну из которых введен постоянный сдвиг фазы на 90°. Сумма сигналов С/А-кода и навигационного сообщения модулирует сдвинутую на 90^о несущую L1, а сумма сигналов Р-кода и навигационного сообщения модулирует несдвинутую несущую L1 и несущую L2. Разделение несущей L1 на две части, модулированные различными кодами, облегчает раздельное выделение C/A-кода и Р-кода в приемной аппаратуре пользователя. После формирования фазоманипулированных сигналов на обеих несущих эти сигналы объединяются при помощи соответствующих электронных устройств в один сигнал сложного состава, который излучается антенной системой спутника.

Дальномерные коды. Дальномерным кодом называют последовательность сигналов, могущих находиться в двух различных состояниях, которым условно приписывают значения 0 и 1. Эти состояния чередуются случайным образом, но через определенные интервалы времени такое чередование периодически повторяется. Подобные последовательности называются псевдослучайными и образуют псевдослучайные коды. На спутнике и в приемнике генерируются совершенно одинаковые коды, которые оказываются сдвинутыми по времени. Период повторения псевдослучайных последовательностей (длительность кода) существенно различен для “грубого” и “точного” кодов. Так, в GPS C/A-код повторяется каждую миллисекунду, а длительность Р-кода составляет 266,4 суток. Короткая длительность C/А-кода позволяет легко захватить сигнал спутника на частоте L1. Намного труднее осуществить захват спутникового сигнала на несущей L2, которая модулирована только Р-кодом. Его чрезвычайно большая длительность выбрана разработчиками специально с целью затруднить доступ к нему для несанкционированных пользователей. Общая длительность Р-кода разбита на недельные отрезки, распределенные по всем спутникам системы, т.е. Р-код каждого спутника повторяется через неделю. Для создания еще большей защищенности вводится так называемое Y-кодирование (режим AS - Anti-Spoofing, что буквально переводится как “противодействие попытке обмана”). Y-код математически может быть описан умножением Р-кода на нелинейную функцию W(t), неизвестную несанкционированным пользователям. Фактически Y-кодирование -это обмен недельными отрезками Р-кода в последовательности, известной только персоналу системы. Правда, в настоящее время фирмы-производители приемной аппаратуры добились на коммерческой основе разрешения вводить в компьютер приемника соответствующую микросхему, реализующую алгоритм отыскания функции W(t).

Принцип построения генератора дальномерного кода. Генераторы дальномерных кодов строятся на основе так называемых сдвиговых регистров с обратными связями. Такой регистр представляет собой набор последовательно соединенных бинарных ячеек - элементов с двумя устойчивыми состояниями (типа триггера). Одному из этих состояний приписывается символ 0, другому - 1. Подачей электрического импульса на ячейку эти состояния можно переключать, а подачей импульса по общей для всех ячеек шине - передавать символ на следующую ячейку, т.е. продвигать его на один разряд к выходу. Введя с выхода последней ячейки на вход первой цепь обратной связи с включенным в нее сумматором, получим генератор псевдослучайной последовательности (ПСП). (Сейчас сдвиговые регистры строятся на основе так называемых ПЗС - приборов с зарядовой связью, но для пояснения принципа действия это несущественно).

Поясним сказанное на простом примере трехразрядного регистра (т.е. содержащего три ячейки). Его схема показана на рис.5.3.

Рис.5.3. Трехразрядный сдвиговый регистр с обратной связью

Предположим, что в начальном состоянии во всех трех разрядах записаны единицы. По общей шине подаются тактовые импульсы с частотой f_имп. На первом такте, т.е. при поступлении первого тактового импульса, на сумматор подается единица с выхода первого разряда и единица с выхода третьего разряда. Сумматор осуществляет сложение по модулю 2:

1 + 1 = 0

1 + 0 = 1

0 + 1 = 1

0 + 0 = 0

Следовательно, сложение двух единиц даст 0, который запишется в первый разряд. Одновременно единица, находившаяся в первом разряде, продвинется во второй, единица из второго разряда - в третий, а единица из третьего разряда - на выход. Аналогичным образом будет происходить дело при поступлении 2-го, 3-го и т.д. тактовых импульсов (таблица 5.2).

Таблица 5.2

№ такта	1-й разряд	2-й разряд	3-й разряд	Выход ПСП
0	1	1	1
1	0	1	1	1
2	1	0	1	1 1
3	0	1	0	1 1 1
4	0	0	1	0 1 1 1
5	1	0	0	1 0 1 1 1
6	1	1	0	0 1 0 1 1 1
7	1	1	1	0 0 1 0 1 1 1

На седьмом такте во всех разрядах регистра окажутся те же числа, что и на нулевом такте, и далее полученная кодовая последовательность 0010111 будет периодически повторяться с периодом Т_ПСП (рис.5.4).

Рис.5.4. Кодовая последовательность из 7 символов

Если на рис.5.3 подключить сумматор к выходу не первого, а второго разряда, то последовательность чередования нулей и единиц изменится, но число символов в длительности кода останется прежним (семь). Оно зависит только от количества разрядов.

В общем случае, для регистра, содержащего к разрядов, число символов М в повторяющейся последовательности будет

М = 2^к - 1.

C/A-код спутников GPS формируется при помощи двух сдвиговых регистров, имеющих по 10 разрядов, и число символов C/A-кода составляет

М _C/A = 2¹⁰ - 1 = 1023.

Кодовая последовательность из 1023 символов “движется” с тактовой частотой f_имп = 1,023 Мгц (см. табл.5.1) и занимает во времени 1 мс. Действительно, частоте f_имп соответствует период повторения Т_имп = 1/f_имп ” 1 мкс, т.е. каждый импульс, а, следовательно, и символ, следует за предыдущим через 1 мкс. Значит, длительность последовательности из М символов равна Т_ПСП = Т _имп М = 1 мкс ž 1023 ” 1 мс.

Как уже отмечалось, каждый спутник имеет свой C/A-код. Они различаются только порядком чередования нулей и единиц при сохранении обшейдлительности. Это достигнуто тем, что на сумматор подаются сигналы от различных пар ячеек регистра.

Генератор Р-кода устроен сложнее - в нем вместо двух используется четыре 10-разрядных регистра. Особенностью работы по Р-коду длительностью 7 суток является то, что для вхождения в синхронизм (для захвата спутника) требуется знать точное время по часам приемника, что дает возможность приближенно предсказать сдвиг местной (генерируемой в приемнике) ПСП относительно ПСП, приходящей от спутника.

В системе ГЛОНАСС опорный генератор имеет частоту, в два раза меньшую по сравнению с GPS (5 Мгц). Символы СТ-кода передаются с тактовой частотой 511 кГц и имеют период повторения 1/511 кГц ” 2 мкс. Используется 9-разрядный сдвиговый регистр, и количество символов в коде составляет М_СТ = 2⁹ - 1 = 511, а длительность кода равна 2 мкс ´ 511 ” 1 мс, т.е. такая же, как в GPS.

Навигационное сообщение содержит 1500 бит и занимает 30 секунд. Оно разделено на 5 субкадров по 300 бит, каждый из которых передается в течение 6 секунд. Субкадр состоит из 10 слов по 30 бит.

Каждый субкадр начинается с телеметрического слова TLM (Telemetry Word), содержащего диагностическое сообщение о состоянии спутника. Вторым словом каждого субкадра является так называемое ключевое слово, обозначаемое HOW (Hand-over Word, буквально - “слово, передаваемое из рук в руки”). Это слово содержит метку времени (так называемый Z-отсчет), записанную в виде 29-разрядного числа в двоичном коде.

Остальная информация распределяется по субкадрам следующим образом:

Субкадр 1 содержит данные о поправке часов спутника относительно системного времени GPST и коэффициенты, заложенные в модель задержки радиосигнала при прохождении его через ионосферу. Информация об ионосфере предназначена только для абонентов, использующих одночастотные приемники (принимающие только частоту L1). При наличии двухчастотного приемника влияние ионосферы практически исключается так называемым дисперсионным способом (см. раздел “Задержка сигнала в атмосфере”).

Субкадры 2 и 3 содержат эфемериды транслирующего спутника, полученные по данным наземных станций слежения. Они корректируются каждый час, но остаются в силе в течение еще некоторого дополнительного интервала времени (по крайней мере в течение получаса) и позволяют вычислить текущие координаты спутника на момент измерения псевдодальности. Эфемериды включают в себя элементы кеплеровой орбиты (см. курс астрономии или космической геодезии) на опорный момент и поправки к ним, позволяющие прогнозировать элементы орбиты внутри периода действия эфемерид.

Субкадр 4 зарезервирован для передачи информации служебного характера, и приемники гражданских пользователей лишены возможности ее получения.

Субкадр 5 содержит альманах спутников и данные об их работоспособности. Альманах - это приближенные эфемериды всех спутников системы. Альманах используется для планирования измерений.

Информация, закладываемая в субкадры 4 и 5, не помещается в одном навигационном сообщении, и эти субкадры разделены на 25 страниц. В каждом сообщении передается одна из этих страниц, так что на передачу всей информации 4-го и 5-го субкадров затрачивается 30 с ´ 25 = 750 с = 12,5 мин.

Кодовые измерения

При кодовых измерениях, как уже отмечалось ранее, измеряемой величиной является время распространения t _р сигнала от спутника до приемника, в которое входит как задержка в атмосфере, так и совокупное отклонение часов спутника и приемника от системного времени. Это время измеряется путем корреляционной обработки кодовых сигналов.

Сущность корреляционной обработки. Понятие “корреляционная обработка” применяется к широкополосным сигналам, т.е. к сигналам, обладающим широким спектром. К таким сигналам относится, в частности, и синусоидальный сигнал несущей, модулированный кодовой (псевдослучайной) последовательностью, и сам кодовый - модулирующий - сигнал, представляющий собой последовательность прямоугольных импульсов различной длины.

Если имеются два одинаковых, но сдвинутых по времени на некоторую величину t широкополосных сигнала S₁ (t) и S₂ (t + t), то вводится понятие корреляционной функции этих сигналов К_1.2, равной

К_1.2 = < S₁ (t)ž S₂ (t + t)>, (6.1)

 

где угловые скобки означают усреднение за большой период времени - такой, который больше периода самой низкочастотной составляющей спектра сигналов S₁ и S₂. Эта корреляционная функция имеет один резко выраженный максимум при t = 0. Следовательно, если изменять задержку t до получения максимума корреляционной функции, мы тем самым измерим эту задержку. Этот принцип и положен в основу кодовых измерений времени распространения.

Рис.6.1. К принципу кодовых измерений с корреляционной обработкой сигнала

В приемнике формируется точно такой же псевдослучайный код, которым модулирован спутниковый сигнал. Этот код (назовем его местным кодом) и приходящий от спутника сигнал подаются на коррелятор (рис.6.1), обеспечивающий переворот фазы приходящего несущего колебания на 180^о в моменты смены символов местного кода. Тогда, если изменять задержку местного кода относительно кода, содержащегося в спутниковом сигнале, то, когда эта задержка станет равной нулю, на выходе коррелятора возникнет немодулированное колебание несущей частоты, ибо при совпадении кодов к 180^о- ным сдвигам фазы несущей от “спутникового” кода будут в те же моменты добавляться 180^о-ные сдвиги от местного кода, а значит, общий сдвиг фазы несущей будет 360^о (нулевой), т.е. фазовая манипуляция снимается. При этом мощность сигнала на выходе фильтра резко возрастает (что соответствует максимуму корреляционной функции). Таким образом, появление немодулированного колебания служит индикатором совпадения “спутниковой” и местной кодовых последовательностей, которые были сдвинуты во времени. Эта временная задержка и измеряется при сдвиге местного кода относительно спутникового до их совпадения. Здесь, однако, надо иметь в виду одно существенное обстоятельство. Если мы работаем по грубому коду (С/А-коду в GPS или СТ-коду в ГЛОНАСС), то мы можем таким способом измерить задержку только в пределах временной длительности этого кода (его периода повторения Т_ПСП), которая составляет в обеих системах 1мс. Интересующее же нас время распространения t _р намного больше одной миллисекунды. Его можно представить в виде

t _р = Nž 1мс + D t, (6.2) где D t - это то, что мы можем измерить (0 < D t < Т_ПСП =1мс), а N - неизвестное целое число миллисекунд во времени t_р. То есть при длительности кодовой посылки, меньшей подлежащего измерению временного интервала, возникает проблема неоднозначности, как при фазовых измерениях. Но здесь она решается без особых трудностей. За 1мс радиоволна проходит 300 км. Число миллисекунд во времени распространения равно числу 300-километровых отрезков в расстоянии до спутника. Мы знаем, что это расстояние составляет примерно 20 000 км, но чтобы верно определить целое число N, расстояние до спутника надо знать с ошибкой менее 150 км. Для этого достаточно вычислить его по координатам спутника и приближенным координатам наземной станции. Таким образом можно получить N и затем найти полное время t _р.

При использовании точного кода проблемы неоднозначности не возникает, так как его временная длительность заведомо больше времени распространения t _р.

Определив t _р и умножив его на скорость света в вакууме, получают псевдодальность, описываемую формулой (3.5) раздела 3:

Р = r + с D t_атм + с D t_ч.

Задержку сигнала в атмосфере D t_атм обычно подразделяют на задержку в тропосфере и задержку в ионосфере. Подробнее это будет рассмотрено в разделе “Задержка сигнала в атмосфере”. Кроме задержек по времени, при распространении сигнала в атмосфере имеет место рефракционное удлинение траектории из-за искривления пути волны в неоднородно-преломляющей среде. Этот эффект отсутствует только на вертикальных трассах (спутник в зените) и возрастает с увеличением зенитного расстояния до спутника.

Определение координат из кодовых измерений. Запишем полученную из кодовых измерений псевдодальность в виде:

Р = r + D _т + D _и + с D t_ч, (6.3) где члены D _т и D _и - выраженные в линейной мере суммарные “вклады” тропосферы и ионосферы соответственно, обусловленные как задержками, так и рефракционным удлинением траектории. Эти величины могут быть учтены (вычислены) - с определенной степенью точности - по известным формулам, основанным на использовании некоторых стандартных моделей (при измерении двухчастотным приемником величина D _и может быть практически исключена). Во всяком случае, эти величины в формуле (6.3) можно полагать известными. Неизвестными остаются r и D t_ч.

Дальность r связана с геоцентрическими координатами приемника X,Y,Z и спутника X_S, Y_S, Z_S известным из аналитической геометрии соотношением:

r = [ (X_S - X)² + (Y_S - Y)² + (Z_S - Z)² ] ^1/2. (6.4)

Координаты спутника X_S,Y_S, Z_S получают по эфемеридным данным, которые при помощи сектора управления и контроля закладываются в навигационное сообщение, транслируемое со спутника на приемник, т.е. X_S, Y_S, Z_S можно считать известными. Поэтому уравнение (6.3) фактически содержит четыре неизвестных - три координаты приемника (определяемого пункта) X,Y,Z и относительный уход часов D t_ч. Если выполнить ОДНОВРЕМЕННО измерения псевдодальностей до четырех спутников (условие одновременности необходимо для обеспечения неизменности величины D t_ч - при этом предполагается, что шкалы времени всех спутников синхронизированы при помощи наземного сектора управления), то мы получаем систему четырех уравнений вида (6.3) с четырьмя неизвестными, из решения которой и находятся искомые координаты пункта X,Y,Z.

Дифференциальный метод кодовых измерений. Описанным выше способом, иногда называемым автономным, можно получить координаты с погрешностью в диапазоне 10-100 м. Существенно увеличить точность можно применением так называемого дифференциального метода. Это - метод с использованием двух наземных станций (приемников). При этом одна из них устанавливается на пункте с известными координатами и называется базовой, опорной или референц-станцией. Другая станция является подвижной. Суть дифференциального способа сводится к следующему. Приемник базовой станции непрерывно работает в Р-коде, и измеренные им псевдодальности сравнивают с “эталонными” расстояниями, вычисленными по координатам. Получаемые разности, называемые дифференциальными поправками, передают на подвижной приемник для коррекции измерений. При этом предполагается, что многие погрешности одинаково влияют на измерения с обеих станций. Чем меньше расстояние между станциями, тем это предположение выполняется точнее. Например, при расстоянии менее 10 км влияние атмосферы можно считать совершенно одинаковым - радиоволны от спутника, находящегося в 20 000 км, проходят расстояния до двух разнесенных на 10 кмприемников практически в одних и тех же атмосферных условиях.

Дифференциальный метод выводит точность кодовых измерений в диапазон от нескольких метров до нескольких дециметров. Существует целая сеть (более 500 в разных странах) базовых станций, передающих дифференциальные поправки в стандартном международном формате RTCM для всех заинтересованных пользователей (бесплатно или на коммерческой основе).

Фазовые измерения

Обратимся теперь к геодезическому режиму работы глобальных систем - фазовым измерениям на несущей частоте. В этом случае измеряется не время распространения сигнала от спутника до приемника, а сдвиг фазы колебаний несущей частоты (излучаемой спутником) за это время, но - и это создает главную проблему - не полный сдвиг j _SR, связанный с расстоянием от спутника S до приемника R, а лишь его дробная часть, меньшая 2p. Это та же проблема разрешения неоднозначности, которая возникает и в наземных фазовых дальномерах. Измеряемый сдвиг фаз реализуется в приемнике как разность фаз между сигналом, принятым от спутника, и опорным сигналом, генерируемым в приемнике. Здесь также возникают проблемы, связанные с разночастотностью сигналов из-за движения спутника (эффект Допплера) и трудностью согласования начальных фаз (синфазирования) спутникового и опорного сигналов, но сейчас мы отвлечемся от этих проблем. Предположим, что для какого-то фиксированного момента времени мы измерили дробную часть фазового сдвига D j. Но, чтобы определить расстояние, нам нужен полный фазовый сдвиг, который равен

j _SR = 2p N + D j = w t _р = 2p f (P/ c), (7.1)

где N - неизвестное целое число, f - несущая частота, Р - псевдодальность, содержащая геометрическое растояние r. Из (7.1) легко получить, учитывая, что с /f = l (длина волны в вакууме):

Р = l N + l (D j /2p). (7.2)

Это почти та же псевдодальность, что и при кодовых измерениях, и ее можно представить выражением вида (6.2), но с двумя характерными отличиями. Во-первых, ионосферный член D _и при фазовых измерениях будет иметь другой знак (см. раздел о влиянии атмосферы). А во-вторых, величина D t_ч, фигурирующая в (6.2), будет иметь несколько другую трактовку. При кодовых измерениях она отражает несинхронность хода часов спутника и приемника. При фазовых же измерениях она является причиной несинфазности (несовпадения начальных фаз) колебаний опорных генераторов спутника и приемника, которую мы будем обозначать через d j. Именно наличие величины d j приводит к тому, что мы и из фазовых измерений получаем псевдодальность. Разумеется, D t_ч и d j жестко связаны друг с другом (d j = 2p f ž D t_ч), поскольку, вследствие единства эталона времени и частоты, “часы” - это и есть генераторы колебаний.

В литературе часто употребляют выражения “кодовая псевдодальность” и “фазовая псевдодальность”. Придадим им индексы “к” и “ф” и запишем, с учетом сделанных замечаний, в виде:

Р_к = r + D _т + D _и + с D t_ч, (7.3)

Р_ф = r + D _т - D _и + c (d j /2p f). (7.4)

Приравнивая (7.2) и (7.4), определим величину D j /2p, обозначая ее через Ф (измеренная величина разности фаз, выраженная в долях цикла - то, что в наземной фазовой дальнометрии обозначают как D N):

Ф = (r /l) - N + (D _т/l) - (D _и/l) + (d j /2p). (7.5)

Присутствие неизвестного целого числа N приводит, как уже упоминалось, к проблеме разрешения неоднозначности.

Обычно в литературе уравнение фазовых измерений используют в виде, аналогичном (7.5).

Если мы каким-то образом определили число N, то можно получить измеренное значение фазовой псевдодальности Р_ф. Однако она содержит неизвестную величину d j. азовые измерения с двумя приемниками позволяют исключить эту величину, используя так называемый метод фазовых разностей.

Метод фазовых разностей. Для исключения d j достаточно выполнить измерения не до четырех, как при кодовых измерениях, а только до двух спутников. Величину d j можно представить разностью d j _S - d j _R (т.е. разностью начальных фаз колебаний генераторов на спутнике и в приемнике). Если выполнить наблюдения одного и того же спутника одновременно двумя разнесенными на некоторое расстояние приемниками, то в разности двух уравнений вида (7.5) исключается величина d j _S для наблюдаемого спутника. Если выполнить теми же приемниками и в ту же эпоху наблюдение второго спутника, то в разности исключается величина d j _S для этого второго спутника. Если теперь составить разность разностей - так называемую вторую или двойную разность (обозначим ее D Ф_II) - то исключается величина d j _R для обоих приемников. Геометрия измерений показана на рис.7.1.

Рис.7.1. Геометрия наблюдений для получения второй фазовой разности

Таким образом, в двойных разностях ликвидируется крупный недостаток одностороннего (беззапросного) фазового метода линейных измерений - неизвестное различие начальных фаз колебаний на спутнике и в приемнике. Поэтому способ двойных разностей является основным при высокоточных геодезических измерениях.

Однако этот способ не ликвидирует другого крупного недостатка фазовых измерений - необходимости разрешения неоднозначности. Но, тем не менее, он кое-что дает и в этом смысле. А именно: так как в двойной разности исключаются начальные фазы колебаний спутника и приемника, то присутствующая в ней “двойная разность” целых чисел (N_А - N_В)^S1 - (N_А - N_B)^S2, соответствующих наблюдениям спутников S1 и S2 приемниками А и В, теоретически действительно является числом целым, что дает основание при обработке округлять его до целого числа, которое обозначают обычно N_o и называют параметром многозначности.

Заметим, что если повторить вышеописанную процедуру наблюдения двух спутников двумя приемниками в другой момент времени, т.е. когда эти спутники займут другое положение, и так же получить двойную разность, а затем составить разность двойных разностей (ее называют третьей или тройной разностью - D Ф_III), то неоднозначность, как часто говорят, исключается. На самом деле это не так: неоднозначность в этом случае не исключается, а, так сказать, игнорируется. Суть дела здесь состоит в том, что при образовании тройной разности в нее входят не сами расстояния между спутниками и приемниками, а их приращения за время перемещения спутников по орбите. Соответственно в третьей разности фигурируют не неизвестные значения N фазовых циклов, а их приращения D N. Эти приращения могут измеряться по показаниям фазометрического устройства при непрерывном отслеживании сигнала спутника. В принципе возможна процедура определения полных значений N по их приращениям с использованием третьих разностей, но она дает весьма низкую точность. Тем не менее она часто применяется при обработке измерений как приближенный вспомогательный метод, позволяющий исключить параметр многозначности N_o. Точное же нахождение целых чисел N (по всем расстояниям), представляющих собой количество уложений волн на пути от спутника до приемника (при длине пути порядка 20 000 км

Предыдущая1234567Следующая

Поделиться:

Воспользуйтесь поиском по сайту: