Задержка сигнала в атмосфере

Общие соотношения. Установим сначала общее выражение для задержки сигнала в атмосфере. Электромагнитная волна проходит элементарный путь dx за время dt = dx/v(x), а весь слой атмосферы толщиной L- за время

t_атм = 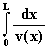= 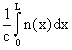, (10.1)

где х - текущее расстояние, v(x) - скорость в атмосфере, n(x) - показатель преломления, с - скорость света в вакууме. Если бы атмосферы не было (n = 1), то тот же геометрический путь L в вакууме был бы пройден за время

t_вак = 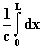10.2)

Отсюда временная задержка, обусловленная наличием атмосферы, равна

D t_атм = t_атм - t_вак = 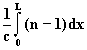(10.3)

Задержка D t_атм, как мы уже знаем, состоит из двух составляющих - недисперсионной (задержка в тропосфере) и дисперсионной (задержка в ионосфере). Обе этих задержки определяются соотношением (10.3), в котором n = n(x) берется соответственно для тропосферы или ионосферы и соответственно устанавливаются пределы интегрирования.

Задержка в тропосфере. В тропосфере обычно вместо показателя преломления n используется индекс преломления N, связанный с показателем простым соотношением: N = (n - 1)ž 10⁶. Индекс преломления показывает, на сколько миллионных долей (единиц шестого знака) показатель преломления воздуха больше единицы. Так, если n = 1,000322, то N = 322. С использованием индекса преломления формула (10.3) применительно к тропосфере получает вид:

D t_троп = (10^-6/с) 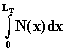(10.4)

где L_T - верхняя граница тропосферы.

Функция N(x) под знаком интеграла - это закон распределения индекса преломления вдоль трассы, который точно никогда не известен. Его аппроксимируют той или иной моделью тропосферы - зависимостью индекса преломления от высоты, т.е. функцией N(H). Модель содержит значение N_o на поверхности Земли в точке установки приемника и предполагаемый закон уменьшения этого значения с высотой в виде некоторой функции, на которую умножается N_o:

N(H) = N_ož F(H). (10.5)

Значение N_o определяется по измерениям температуры Т, давления Р и влажности воздуха е с использованием хорошо известной формулы.

Это дает возможность получить вертикальное распределение индекса преломления. Для учета наклона трассы используют выведенные теоретически зависимости модели от зенитного расстояния z. По описанному принципу построена распространенная модель Хопфилд, применяемая в GPS. Существуют и другие подходы - без использования зависимости N(H). Такова, например, модель Саастамойнена (принятая при работе с ГЛОНАСС), содержащая параметры Т, Р, е и z.

Тропосферная задержка, выраженная в линейной мере (т.е. величина с D t_троп), лежит в диапазоне от примерно 2,4 м при z = 0 (спутник в зените) до более 10 м при z = 80^o. При z > 80^o, т.е. когда угол возвышения над горизонтом меньше 10^о, наблюдений не производят.

Учет задержки сигнала в тропосфере по соответствующим формулам дает некоторую остаточную погрешность, обусловленную несовершенством тропосферных моделей. Наиболее полно учитывается влияние тропосферы при дифференциальных и относительных измерениях при длине базы до 10-15 км. В этом случае атмосферные условия для сигналов, приходящих от спутника на оба приемника, считаются практически одинаковыми, и остаточное влияние тропосферы дает погрешность в пределах нескольких сантиметров.

Задержка в ионосфере. Как уже отмечалось в предыдущем разделе, ионосфера для радиоволн является диспергирующей средой. В таких средах понятие скорости распространения теряет свою однозначность: приходится различать понятия фазовой скорости и групповой скорости.

Фазовая скорость - это скорость распространения фазы монохроматической волны - волны, имеющей строго одну частоту. Фазовой скорости v_фсоответствует фазовый показатель преломления n_ф = с/ v_ф. Реальный сигнал имеет конечный спектр, т.е. состоит из многих составляющих различных частот, образующих группу волн. Каждая из этих составляющих - в этом и заключается явление дисперсии - распространяется со своей фазовой скоростью. Зависимость v_ф от частоты f приводит к необходимости введения такого понятия, которое характеризовало бы распространение группы волн как целого. Таким понятием и является групповая скорость. Она характеризует перенос энергии группой волн.

Групповая скорость - понятие, применимое лишь к случаю узкого спектра D f (т.е. когда D f << f) и к среде со слабой дисперсией, так как только при таких условиях группа волн при распространении не деформируется и поэтому можно говорить о ее скорости. Групповой скорости v_грсоответствует групповой показатель преломления n_гр = с/ v_гр.

При модуляции гармонического колебания частоты f всегда возникает спектр шириной D f = 2F, где F - частота модуляции. При этом можно считать, что в среде с дисперсией несущее колебание частоты f распространяется с фазовой скоростью, а огибающая, воспроизводящая форму модулирующего сигнала, распространяется с групповой скоростью. В частности, это имеет место и в интересующем нас случае распространения спутникового сигнала в ионосфере. При фазовых измерениях мы имеем дело с несущими гармоническими колебаниями (на частотах L1 и L2), распространяющимися с фазовыми скоростями, и, следовательно, при расчете задержки в ионосфере в этом случае должен фигурировать фазовый показатель преломления. При кодовых же измерениях мы имеем дело с кодовыми сигналами, которые модулируют несущие колебания и, значит, характеризуются групповой скоростью распространения. В этом случае при расчете задержки должен использоваться групповой показатель преломления ионосферы.

Для фазового и группового показателей преломления ионосферы установлены соотношения, которые могут быть записаны в следующем приближении (без учета влияния магнитного поля Земли):

n_ф = 1 - 40,4 ,(10.6)

n_гр = 1 + 40,4 , (10.7)

где f - частота, N_e - электронная концентрация, выражаемая числом свободных электронов в единице объема. Если f брать в килогерцах, то N_eбудет иметь размерность [эл/см³] .

Обратим внимание на любопытное обстоятельство: как видно из приведенных формул, в ионосфере фазовый показатель преломления меньше, а групповой - больше единицы на одну и ту же величину. Если nф < 1, это означает, что фазовая скорость волны в такой среде больше с - скорости света в вакууме. Групповая же скорость меньше с на такую же величину. Поэтому при фазовых и кодовых измерениях задержки в ионосфере будут одинаковы по величине, но различны по знаку: при фазовых измерениях задержка отрицательна, а при кодовых - положительна.

Подставляя определяемые из соотношений (10.6) и (10.7) величины (n_ф - 1) и (n_гр - 1) в общее выражение (10.3), получим для задержек в ионосфере:

При фазовых измерениях: D t_ион = , (10.8)

При кодовых измерениях: D t_ион = 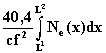, (10.9)

где L₁ и L₂ - нижняя и верхняя границы ионосферы. Интеграл в зарубежной литературе принято обозначать аббревиатурой ТЕС (TotalElectron Content - интегральная электронная концентрация). По порядку величины ТЕС составляет примерно 3ž10¹³ эл/см², но это весьма приближенное значение, так как ТЕС может изменяться в широких пределах в зависимости от времени суток, сезона года, широты места наблюдения и др. Вычисление этого интеграла - сложная, а главное - не поддающаяся точному решению задача. Предложено несколько моделей для ее приближенного решения, из которых наибольшее распространение получила модель Клобучара. Рассчитанные по этой модели задержки лежат в пределах 15-150 нс, что дает в линейной мере поправки к псевдодальностям в диапазоне примерно 5-50 метров. Однако погрешность этих поправок может составлять несколько метров. Поэтому модельный способ учета влияния ионосферы применяется в основном в навигации при абсолютном методе определения координат, а в геодезии - при работе на базах, не превышающих 10 км, когда ионосферные условия для радиоволн, приходящих на оба приемника, практически одинаковы. В этом случае даже измерения только на частоте L1 (с одночастотными приемниками) с использованием модельного учета может дать неплохие результаты. При точных геодезических измерениях применяют метод, основанный на использовании двух несущих частот L1 и L2.

Двухчастотный метод учета влияния ионосферы. Он основан на зависимости показателя преломления ионосферы от частоты, т.е. на дисперсии, и потому является дисперсионным методом. Укажем здесь лишь на основной его принцип, не приводя подробных математических выкладок. При выполнении фазовых измерений на двух несущих частотах можно записать два уравнения вида (7.5) для фаз Ф_L1 и Ф_L2, в которых будут фигурировать соответственно числа N₁ и N₂ и длины волн l ₁ и l ₂. Если в этих уравнениях учесть зависимость ионосферных членов от частоты на основе формулы (10.8), а затем умножить уравнение для Ф_L2 на отношение частот f_L2/f_L1, то ионосферный член в нем окажется таким же, как и в уравнении для Ф_L1, и разность

Ф₁₂ = Ф_L1 - Ф_L2 (10.10) будет свободна от ионосферного члена.

Подобный принцип можно применить и к кодовым измерениям. В этом случае будем иметь два уравнения вида (6.3) для псевдодальностей Р_L1 и Р_L2, и второе из них надо умножить на отношение квадратов частот. Тогда разность

Р₁₂ = Р_L1 - P_L2 (10.11) будет также свободна от ионосферного члена.

Таким образом, измерения на двух частотах дают возможность получить расстояние, практически свободное от влияния ионосферы. Именно для этого в спутниковом сигнале предусмотрена вторая несущая и все высокоточные приемники являются двухчастотными.

Некоторое остаточное влияние ионосферы обусловлено недостаточной строгостью формул, отражающих зависимость показателя преломления ионосферы от частоты. Соответствующая погрешность мала и находится на уровне нескольких миллиметров.

Предыдущая1234567Следующая

Поделиться:

Воспользуйтесь поиском по сайту: