Расчет технических требований на конструкцию изделия

 

Качество детали определяется соответствием ее фактических данных проектным в отношении материала и термической обработки, геометрических форм, размеров детали, качества обрабатываемых поверхностей.

Ко всем перечисленным факторам предъявляются определенные технические требования:

а) технические условия на материал и термическую обработку (если она необходима);

б) допуски на геометрическую форму (цилиндричность, параллельность, концентричность и т.п.);

в) допуски на размеры деталей;

г) параметры шероховатости поверхностей.

Таким образом, каждая деталь машины должна быть изготовлена с определенной степенью точности, пределы колебаний которой определяются конструктором при проектировании.

Аналогично операциям механической обработки операции сборки также должны выполняться с определенной степенью точности. В связи с этим собранные узлы и машины в целом должны соответствовать заранее разработанным техническим условиям.

Разрабатывая новую конструкцию какого - либо изделия, конструктор сопровождает ее целым рядом технических условий на изготовление. Часть из них он выбирает из соответствующих стандартов, другие получает в результате расчетов. Нередко конструктор задает ТУ, исходя не из довольно - таки громоздких расчетов, а собственного опыта и интуиции. При этом желая подстраховаться, он необоснованно ужесточает величины допусков ряда параметров, что приводит к усложнению технологического процесса изготовления изделия, увеличению его себестоимости и, соответственно, снижению конкурентоспособности на рынке. Чтобы избежать этого, необходимо при анализе ТТ на изготовление изделия проводить расчет и сравнение некоторых особо точных заданных параметров.

 

Порядок расчета

 

Рассмотрим примерную последовательность выполнения таких расчетов. Для всех случаев определены следующие общие начальные этапы расчета.

1. Выявляют исходные размеры и устанавливают предъявляемые к ним требования точности (t_å, em_å, еs_å, ei_å).

2. Выявляют влияющие размеры.

3. Составляют конструктивные схемы изделия и его составных частей, на которых указывают исходный и влияющие размеры.

4. Определяют коэффициенты С_i влияющих размеров.

5. Определяют или принимают значения коэффициентов относительной асимметрии a или относительного рассеивания k влияющих размеров.

6. По каждой расчетной схеме определяют метод достижения требуемой точности исходного размера.

Если по конструкции изделия для какой-либо расчетной схемы этот метод нельзя определить сразу, то на влияющие размеры такой схемы назначают ориентировочные допуски t_i и определяют приближенное значение расчетного допуска исходного размера по формуле

t_å¢ = 1,2 i²ti².

Если t_å¢ >> t_å, то требуемую точность исходного размера следует обеспечивать по методу компенсации, а если t_墻 t_å - по методу взаимозаменяемости. Определяют очередность расчета связанных расчетных схем.

7. Увязывают номинальные значения размеров и определяют расчетный номинальный исходный размер Y_å¢.

Последующие этапы зависят от методов расчета достижения требуемой точности. Точность сборочных единиц изделий машиностроения зависит от точности изготовления деталей. Показатель точности сборочной единицы Y_S связан с размерами деталей линейной функцией

Y_å = Y_{i ,} (3.1)

где Y_i –показатель точности детали, являющийся аргументом функции и называемый также влияющим размером;

C_i –постоянная при случайной величине Y_i, называемая в дальнейшем коэффициентом приведения.

Он задается техническими требованиями и является исходным для расчета допусков, поэтому размер Y_å называют также исходным размером. При сборке изделия размер Y_å формируется последним, поэтому его называют иногда конечным или замыкающим размером. Влияющие и исходные (конечные) размеры, входящие в функцию (3.1), часто изображают в виде схемы размеров.

Согласно [63], среднее отклонение исходного размера можно определить из зависимости

em_å = åc_i(em_i+ a_it_i) - a_åt_å. (3.2)

Произведя некоторые преобразования, получаем допуск исходного звена

t_{å =} 1\k_å . (3.3)

При отсутствии корреляции между случайными величинами

t_å = 1\k_å . (3.4)

В этих формулах: em_i и t_i -среднее отклонение и допуск влияющего i -го размера;

a_i и k_i - коэффициенты относительной асимметрии и относительного рассеивания i -го влияющего размера;

C_i и С_j - коэффициенты приведения;

r_ij - коэффициент корреляции;

em_å и t_å - среднее отклонение и допуск исходного размера;

a_å и k_å - коэффициенты относительной асимметрии и относительного рассеивания исходного размера.

Числовые значения коэффициентов a_å и k_å зависят от функции распределения конечного размера, которую находят компонированием функций распределения влияющих размеров.

В конечном итоге функция распределения исходного размера определяется числом влияющих размеров, составляющих расчетную схему; законами их распределения; соотношением допусков влияющих размеров.

Известно, что при компонировании двух равновероятных распределений с одинаковыми допусками суммарное распределение подчинено закону Симпсона (рис. 3.20, а). При компонировании двух распределений по закону Симпсона суммарное распределение мало отличается от закона Гаусса (рис. 3.20, б). Если компонировать два асимметричных закона (рис. 3.20, в), то суммарная функция сглаживается, а величина асимметрии уменьшается. При компонировании двух таких сглаженных функций суммарное распределение оказывается близким к нормальному (рис. 3.20, г).

Следовательно, при увеличении в расчетной схеме числа влияющих размеров суммарное распределение конечного размера стремится к симметричному распределению по закону Гаусса.

На основании изложенного коэффициента a_å и k_å принимают по следующим рекомендациям.

Принимают коэффициент относительной асимметрии a_å = 0, если выполняется одно из условий:

- коэффициенты влияющих размеров a_i = 0;

- среди влияющих размеров с любыми законами распределения есть два или более размера, имеющих a_i = 0 и доминирующие допуски;

- среди влияющих размеров с любыми законами распределения имеется пять или более размеров с однородными по величине допусками (под однородными по величине считают допуски, различающиеся примерно на 30 %).

Принимают коэффициент относительного рассеивания k_å = 1,0, если выполняется одно из условий:

- коэффициенты влияющих размеров k_i = 1,0;

- среди влияющих размеров с любыми законами распределения есть два или более размера, имеющих k_i = 1,0 и доминирующие допуски;

- среди влияющих размеров с любыми законами распределения имеется пять или более размеров с однородными по величине допусками.

Если перечисленные условия не выполняются, то приближенные значения коэффициентов a_å и k_å вычисляют по следующим формулам:

a_å = 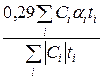, (3.5)

k_å = 1+ 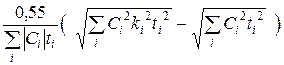. (3.6)

Точность коэффициентов a_å и k_å, определяемых по этим формулам, для практических расчетов вполне достаточна.

Если необходимо, то более точные значения этих коэффициентов определяют по результатам компонирования функций f(y_i), плотности вероятностей влияющих размеров. Эти функции попарно компонируют (обычно на ЭВМ) и получают в итоге функцию f(y_å) плотности вероятностей конечного размера.

При рассеивании исходного размера по закону Гаусса (или близкого к нему) значения коэффициента k_å = 1 соответствуют 0,27 % выхода исходного размера за пределы поля допуска. Если для каких-либо условий возможен процент выхода, отличный от 0,27 %, то принимают одно из следующих значений k_å (для закона Гаусса):

Процент риска… 0,02 0,05 0,1 0,2 0,27 0,5 1,0 1,5

k_å ……………… 0,81 0,86 0,91 0,97 1,00 1,06 1,16 1,23

Процент риска…2,0 3,0 4,0 5,0 6,0 8,0 10,0

k_å ……………… 1,29 1,38 1,46 1,52 1,60 1,71 1,82

 

Рис.3.20

 

 

3.7.2. Определение коэффициентов приведения

Коэффициент приведения С_i - постоянная, определяющая направление и степень воздействия влияющего размера на конечный.

Все влияющие размеры разделяют на увеличивающие (знак плюс перед коэффициентами C_i); уменьшающие (знак минус перед коэффициентами C_i). Положительное приращение увеличивающего размера вызывает увеличение исходного размера, а также приращение уменьшающего размера - уменьшение исходного размера.

Величину коэффициентов С_i и знак перед ними определяют из рассмотрения расчетной схемы. Расчетные схемы могут содержать размеры: только линейные (параллельно и не параллельно расположенные), только угловые, одновременно и линейные и угловые.

В расчетных схемах с линейными параллельно расположенными размерами коэффициенты С_i для размеров, отклонения которых вызывают поворот осей или поверхностей деталей, определяют как отношение плеч рычагов со знаком плюс для увеличивающих и со знаком минус для уменьшающих размеров. В остальных случаях коэффициенты увеличивающих размеров С_i = 1,0, уменьшающих С_i = -1,0.

На рис. 3.21 приведена расчетная схема, относящаяся к валу барабана, опоры которого расположены в отдельных стойках. Здесь исходный размер A_å - расстояние от основания до центра концевого участка вала барабана; влияющие размеры: А₁ - высота ступеньки основания; А₂ и А₃ - расстояние от оси отверстия до опорной поверхности соответственно правой и левой стойки. Увеличение влияющего размера А₁ увеличивает исходный размер A_å и не приводит к повороту оси барабана, поэтому С₁ = 1,0.

Рис.3.21

 

Изменение влияющего размера А₂ при неизменном А₃, как и изменение А₃ при неизменном А₂, приводит к повороту оси барабана и соответствующему изменению исходного размера А_å. Используя отношение плеч рычагов, получим

 

С₂ = ; (3.7)

 

C₃ = - . (3.8)

Математическое ожидание и дисперсия обобщенной функции определяются по следующим зависимостям

 

; (3.9)

или . (3.10)

Отсюда

 

. (3.11)

В этих формулах М_åi - математическое ожидание;

K_åi²t_åi² - характеристика рассеивания отдельного i-го вида аргумента обобщенной функции.

Для суммы векторных величин с учетом коэффициента приведения найдем

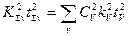. (3.12)

Поскольку в этой зависимости векторные величины представлены в виде смещения осей, то законы их распределения относят не ко всему полю рассеивания, а только к его половине. Приведенный коэффициент относительного рассеивания при распределении модуля вектора по законам нормального распределения или Симпсона колеблется в пределах К_v = 0,7…0,9. Для проектных расчетов можно принимать К_v = 0,75. Тогда окончательно для случая, когда в расчетной схеме кроме векторных имеются другие виды ошибок:

k_åv²t_åv² = 0,75² . (3.13)

Если расчетная схема содержит только векторные величины, то при проектных расчетах суммарный вектор определяют по формуле

t_åv = . (3.14)

 

Коэффициенты 0,75 и 0,85 соответствуют проценту риска 2b = 0,27%. Если брать 2b ¹ 0,27%, то коэффициенты 0,75 и 0,85 умножают на коэффициент С₀, который принимают по следующим данным.

2b, %…0,05 0,10 0,20 0,27 0,50 1,00 2,00 3,00 5,00

С₀ …….1,13 1,07 1,02 1,00 0,95 0,89 081 0,77 0,71.

В формулах (3.12), (3.13) и (3.14) - t_v - допуск модуля влияющего вектора, t_åv - то же, для исходного (суммарного) вектора.

Для схемы на рис. 3.22 коэффициенты влияющих размеров

С₁ = cos b₁ = cos (180-b) = - cosb;

C₂ = cos b₂ = cos(90-b) = sin b;

C₃ = cos b₃ = cos b;

C₄ = cos b₄ = cos(90+b) = - sin b.

Величину и знак коэффициента С_i можно определить также графическим способом, который в ряде случаев более удобен. Воспользовавшись схемой, представленной на рис. 3.23, определим коэффициент С_i для размера B_{1 .} Для этого из произвольной точки проведем прямую параллельно направлению размера B₁ (рис. 3.23, б). В принятом масштабе отложим отрезок аа¢, равный приращению размера B₁. Через точку а проведем прямую I-I, параллельную направлению исходного размера В_å, а через точку а¢ - прямую II-II, перпендикулярную ему. Отношение отрезков аа¢¢/aa¢ - есть величина коэффициента С_i для размера B₁. Из рис. 3.23, а видно, что увеличение влияющего размера B₁ вызывает уменьшение исходного размера В_å. Следовательно, размер B₁ - уменьшающий, и окончательно С₁ = - аа¢¢ / aa¢. Исследуемому размеру можно давать приращение в любом направлении.

 

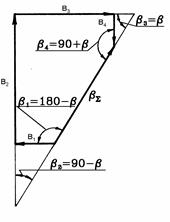
Рис.3.22 Рис.3.23

Подобные построения выполняют и для определения коэффициентов С_i других влияющих размеров.

При анализе расчетных схем, содержащих угловые размеры, предполагается наличие жестких связей между размерами. Тогда изменение, какого-либо углового размера на определенную величину вызывает поворот всех жестко связанных размеров на угол, равный по величине изменению данного размера.

 

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: