Краткие теоретические сведения

Министерство образования и науки РФ

Федеральное государственное автономное образовательное учреждение высшего профессионального образования

«Национальный исследовательский ядерный университет МИФИ»

Обнинский институт атомной энергетики

Факультет кибернетики

А.А. Абакумов, Л.К. Особливец, Е.Г. Типикин

Основы теории электрических цепей

Лабораторный практикум по курсу

«Электротехника и электроника»

 

 

Обнинск 2012

УДК 621.3.06

 

 

Абакумов А.А., Особливец Л.К., Типикин Е.Г. Основы теории электрических цепей. Лабораторный практикум по курсу «Электротехника и электроника». – Обнинск: ИАТЭ НИЯУ МИФИ, 2012, -76с.

В пособии уделено внимание организации и порядку выполнения работ по основам теории электрических цепей в лаборатории «Электротехника», описано типовое оборудование. Cформулирована цель постановки каждой лабораторной работы, изложены основные теоретические положения, описаны схемы установок и даны рекомендации к проведению опытов и обработки результатов эксперимента.

Практикум рассчитан на студентов факультетов К, ФЭФ и ФЕН.

Рецензенты: к.т.н. В.И. Белозеров,

к.т.н. П.К. Лысяков

 

 

Темплан 2012, поз. 30

 

© Обнинский институт атомной энергетики, 2012 г.

© А.А. Абакумов, Л.К. Особливец, Е.Г. Типикин, 2012г.

ВВЕДЕНИЕ

 

Данный лабораторный практикум является составной частью учебно-методического комплекса по курсу «Электротехника и электроника» (раздел «Основы теории электрических цепей»).

В лаборатории осуществляется один из важнейших моментов учебного процесса – связь теории с практикой, в результате чего студенты приобретают необходимые знания, умения и навыки по проведению экспериментов с электрическими цепями и самостоятельной оценке полученных результатов.

Принятое в пособии изложение закрепляет теоретические знания студентов и прививает им умение и навыки по исследованию электрических цепей, измерениям электрических величин и обеспечивает подготовку к самостоятельному выполнению лабораторных работ.

При подготовке к выполнению и защите лабораторных работ по основам теории электрических цепей студенты должны изучить соответствующие разделы учебника, так как приводимые в пособии пояснения недостаточны для полного понимания материала. Также необходимо изучить содержание самой лабораторной работы, ответить на предлагаемые вопросы, начертить схемы исследуемых установок, таблицы для внесения данных измерений.

Изучив правила техники безопасности и будучи допущенными преподавателем к работе, студенты могут приступать к сборке исследуемых схем, подключать измерительные приборы. После проверки преподавателем собранных схем и получения разрешения студенты могут приступать к выполнению лабораторной работы.

По каждой выполненной лабораторной работе студенты должны составить отчет, в котором приводятся краткие теоретические сведения, расчетные формулы, таблицы с рассчитанными и измеренными величинами, их графики, анализ полученных результатов, выводы по работе. Защита лабораторных работ проводится в строго отведенное для этого время.

Данное учебное пособие способствует привитию студентам базовых знаний по разделу «Основы теории электрических цепей», развивает умения и навыки в проведении экспериментов с обработкой и оформлением полученных данных, а также побуждает давать критическую оценку результатам, полученным при постановке опыта.

Пособие предназначено для студентов ИАТЭ, изучающих курс «Электротехника и электроника».

Лабораторная работа № 1

ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ ПОСТОЯННОГО ТОКА

 

Цель работы – получение навыков измерений в цепи постоянного тока.

Краткие теоретические сведения

Электрическая цепь – это устройство, состоящее из источников и потребителей электрической энергии, соединенных проводниками. Источники и потребители – это элементы электрической цепи.

Схема электрической цепи – идеализированное графическое изображение электрической цепи.

Вольтамперная характеристика (ВАХ) – зависимость между напряжением, приложенным к элементу или участку цепи, и протекающим в нем током. Элемент цепи называется линейным, если его вольтамперная характеристика – прямая линия. Линейная цепь состоит только из линейных элементов.

Общая задача анализа электрической цепи состоит в том, что в известной схеме цепи с заданными параметрами (ЭДС и сопротивлениями) необходимо рассчитать токи, напряжения и мощности на отдельных участках. Решение задачи анализа может быть выполнено с помощью разных методов, среди которых наиболее часто используются метод Кирхгофа, контурных токов, узловых потенциалов, эквивалентного генератора. Подробное описание методов можно найти в литературе [1 –5]. Здесь в качестве примера мы ограничимся применением указанных методов к анализу цепи на рис. 1.

Все электрические цепи подчиняются первому и второму законам Кирхгофа.

Первый закон Кирхгофа применяется к узлам электрической цепи. Он гласит: алгебраическая сумма токов в узле электрической цепи равна нулю, т. е.

 

,

где I_k – ток k -ой ветви, присоединенной к данному узлу; n – число ветвей, подключенных к узлу.

Токи, направленные к узлу, записываются со знаком плюс, от узла – со знаком минус.

Второй закон Кирхгофа применяется к контурам электрической цепи. Он формулируется следующим образом: алгебраическая сумма напряжений на сопротивлениях контура равна алгебраической сумме ЭДС в этом контуре:

,

 

где U_k – напряжение на k -oм сопротивлении контура; Е_k – k -ая ЭДС, входящая в данный контур; m – число ЭДС в контуре; n – число сопротивлений в контуре.

Напряжения и ЭДС записываются со знаком плюс, если их направления совпадают с выбранным направлением обхода контура, со знаком минус – в противном случае.

 

 

E 1

 

Рис. 1

 

По методу Кирхгофа в цепи, содержащей пассивные элементы и источники напряжений и имеющей в ветвей, необходимо определить столько токов, сколько ветвей имеет цепь. При этом по первому закону Кирхгофа следует составить (у –1) уравнение, где у – число узлов в цепи, а остальные k = в –(у –1) записать по второму закону Кирхгофа, выбрав k независимых контуров.

Например, для схемы на рис. 1, содержащей пять ветвей и три узла, необходимо составить систему из пяти уравнений, в том числе на основании первого закона Кирхгофа – два уравнения, на основании второго – три:

–I ₁ + I ₂ – I ₄ = 0;

–I ₂ + I ₃ – I ₅ = 0;

R ₁ I ₁ – R ₄ I ₄ = – E ₁;

R ₂ I ₂ +R ₄ I ₄ – R ₅ I ₅ = 0;

R ₃ I ₃ + R ₅ I ₅ = E ₃.

При расчете по методу контурных токов предполагают, что в каждом независимом контуре течет свой контурный ток. Уравнения составляют относительно контурных токов, а ток каждой ветви равен алгебраической сумме контурных токов, замыкающихся через эту ветвь.

Так для цепи, изображенной на рис.1, система уравнений, составленная по методу контурных токов, может быть записана в следующем виде:

По контурным токам определяются токи в ветвях:

I ₁ = I ₁₁; I ₂ = I ₂₂; I ₃ = I ₃₃; I ₄ = – I ₁₁ + I ₂₂; I ₅ = – I ₂₂ + I ₃₃ .

Метод узловых потенциалов заключается в определении потенциалов узлов относительно узла, потенциал которого принимается равным нулю. Так, для схемы рис. 1, система уравнений по методу узловых потенциалов относительно φ _c = 0 может быть записана следующим образом:

 

(1)

Зная потенциалы узлов, определенные из уравнений (1), токи в ветвях определим по закону Ома:

 

;

Экспериментально потенциалы узлов определяются с помощью вольтметра относительно узла, потенциал которого принят за нулевой.

Метод эквивалентного генератора (метод холостого хода и короткого замыкания) дает возможность часть сложной электрической цепи с источниками энергии и двумя выделенными выводами, т.е. активный двухполюсник, заменить эквивалентным генератором, ЭДС которого равна напряжению холостого хода на выводах двухполюсника, и внутреннее сопротивление – выходному сопротивлению двухполюсника.

Так, если требуется определить ток I ₂ в исходной схеме (рис.1), то можно записать

,

где

Опытным путем ток I ₂ может быть определен из двух опытов:

– опыта холостого хода, когда разрывается ветвь «ав» и с помощью вольтметра измеряется напряжение холостого хода U_{ba xx};

– опыта короткого замыкания, когда закорачивается сопротивление R ₂ и с помощью амперметра измеряется в этой ветви ток короткого замыкания I _2кз.

 

Тогда , где .

 

Принцип взаимности основан на теореме взаимности: для любой линейной цели, ток в «k»-ветви, вызванный ЭДС, действующей в «m»-ветви, равен току в «m»-ветви, вызванному ЭДС, действующей в «k»-ветви, при условии равенства ЭДС (Е_k = Е_m).

Так в схеме (рис.1) ток в первой ветви , вызванный ЭДС Е ₂, равен току во второй ветви , вызванному ЭДС Е ₁, если Е ₁= Е ₂.

Опытным путем принцип взаимности следует проверить следующим образом: включив амперметры в правую и левую ветви, установить равные значения ЭДС Е ₁ = Е ₂. Выключив ЭДС Е ₁, измерить ток в первой ветви под действием ЭДС во второй ветви Е ₂, затем, выключив ЭДС Е ₂, измерить ток во второй ветви под действием ЭДС в первой ветви.

При анализе линейных электрических цепей широко используются понятия входной и взаимной проводимостей.

Входная проводимость любой ветви «k» g_kk определяется отношением тока I_k, протекающего в этой ветви, к ЭДС Е_k, расположенной в этой же ветви, при равных нулю ЭДС в остальных ветвях. Взаимная проводимость «k» и «m» ветвей g_km определяется отношением тока I_k, протекающего в ветви «k», к ЭДС Е_m, расположенной в ветви «m», при равных нулю ЭДС в остальных ветвях.

В соответствии с принципом взаимности, очевидно, что g_km = g_mk.

Входными и взаимными сопротивлениями ветвей называются величины, обратные соответствующим проводимостям. Входные и взаимные проводимости и сопротивления ветвей можно определить экспериментально и рассчитать.

Экспериментально входные и взаимные проводимости определяются следующим образом (рис.1):

, , , ,

 

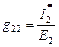где и – токи, измеренные в ветвях с R ₁и R ₂ при действии ЭДС Е ₁; и – при действии ЭДС Е _2.Расчет входных и взаимных проводимостей ветвей можно осуществить несколькими способами. Так, например, их можно определить, составив систему уравнений по методу контурных токов.

Контуры при этом выбираются так, чтобы «k» - ветвь входила только в один контур и ветви, входные и взаимные проводимости которых подлежат определению, входили бы только каждая в свой контур, а в другие контуры не входили.

Входная проводимость ветви может быть определена и как величина, обратная входному сопротивлению цепи относительно данной ветви. Так для схемы рис. 1 входные проводимости расчетным путем можно определить как

, где или,

 

например, , где и т.д.

 

Рабочее задание

1. В исследуемой цепи, схема которой изображена на

рис. 2, определите резисторы, соединенные последовательно и параллельно. Найдите способ зафиксировать это наглядной записью.

 

 

Рис. 2

 

2. На вход исследуемой цепи подайте постоянное напряжение, величина которого указана на макете. Выполните измерения

а) напряжений на всех резисторах;

б) потенциалов в точках 1,2,5 (рис.3);

в) напряжения холостого хода (х.х.) между точками 3 – 4 (рис. 4);

г) токов I ₁ и I ₃ (рис. 3);

д) тока короткого замыкания (к.з.) между точками 2 – 4 (рис. 5).

 

 

Рис. 3

 

 

Рис. 4 Рис. 5

3. Убедитесь в линейности цепи, для чего проведите измерения, необходимые для построения графика зависимости тока I ₃ от напряжения U ₁. Постройте этот график.

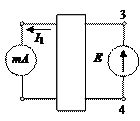
4. Подтвердите экспериментально теорему взаимности, для чего проведите взаимное переключение источника ЭДС и миллиамперметра в ветвях, содержащих резисторы R ₁ и R ₂ (рис. 6). Измерьте величины токов I ₁и I ₃. Убедитесь в том, что в пределах погрешности измерений выполняется равенство I ₁ = I ₃.

 

 

 

Рис. 6

 

5. Запишите для исследуемой цепи систему уравнений Кирхгофа. Проверьте правильность законов Кирхгофа, пользуясь результатами измерений (п. 2).

6. Пользуясь методом контурных токов, рассчитайте токи I ₁и I ₃.

7. Пользуясь методом узловых потенциалов, рассчитайте потенциалы узлов в точках 1, 2.

8. Рассчитайте ток I ₃, заменив цепь относительно нагрузки R ₃ эквивалентным генератором. Определите элементы Е _Э и R _Э того же эквивалентного генератора по данным измерений (п. 2). Сравните полученные результаты. Нарисуйте схему эквивалентного генератора с нагрузкой.

9. Рассчитайте взаимные проводимости g ₁₃= g ₃₁. Сравните полученный результат с величиной взаимной проводимости g ₃₁ = , определенной на основе измерений.

10. На основе выполненных измерений рассчитайте входное сопротивление цепи и потребляемую цепью мощность.

11. Постройте потенциальную диаграмму для контура 4,5,1,2,3,4 (рис. 2).

 

Контрольные вопросы

1. Какие электрические цепи (устройства) постоянного тока с определенными функциональными назначениями Вам известны?

2. Какая электрическая цепь называется линейной? Как изменится ток I ₁, если все сопротивления увеличить в два раза?

3. Что называется ветвью, узлом, контуром электрической цепи?

4. Какая электрическая цепь называется обратимой?

5. В чем отличие источника ЭДС от источника тока?

6. Каковы параметры реального и идеального источников ЭДС и тока?

7. Как перейти от схемы с источником ЭДС к эквивалентной схеме с источником тока?

8. Какие режимы работы электрических цепей Вам известны?

9. Как формулируется обобщенный закон Ома?

10. Как формулируются законы Кирхгофа?

11. Каков порядок расчета цепи методами контурных токов, узловых потенциалов и эквивалентного генератора?

 

 

Лабораторная работа N2

12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: