 |
Краткие теоретические сведения
|
|
|
|
Электрические цепи подобно механическим системам обладают инерционностью. Это приводит к тому, что отклик электрической цепи на внешнее возмущение происходит не мгновенно, а в течение некоторого времени, пока идет переходный процесс – переход цепи от одного устойчивого состояния в другое. Инерционность цепей обусловлена наличием элементов L и С, ограничивающих возможность мгновенного изменения тока в L и напряжения на С.
Знание законов протекания переходных процессов и математических методов их расчета необходимо в тех многочисленных случаях, когда мы интересуемся реакцией электрической цепи на возмущение одиночными или периодическими сигналами несинусоидальной формы. Подобные расчеты производятся несколькими методами: классическим, операторным, спектральным, а также методом с применением интеграла Дюамеля.
В классическом методе электрическая цепь описывается дифференциальным уравнением с правой частью, выражающей внешнее возмущение. Решение определяет искомую реакцию, т.е. вид переходного процесса.
Операторный метод связан с преобразованием временных функций в функции комплексного переменного с помощью интеграла Лапласа. Метод упрощает интегрирование дифференциальных уравнений и сводит описание электрической цепи к алгебраическим уравнениям.
Спектральный метод дает возможность несинусоидальные периодические и одиночные сигналы представить в виде суперпозиции синусоидальных колебаний. В этом случае реакция цепи оценивается путем сопоставления частотных характеристик воздействующего сигнала и цепи. Метод отличается наглядностью и дает возможность проведения качественных оценок.
Метод интеграла Дюамеля заключается в том, что сложный по форме сигнал представляется в виде бесконечно большого числа бесконечно малых, простых по форме сигналов (например, ступенчатых). При этом, зная реакцию цепи на простой сигнал, путем интегрирования находят реакцию на сложный сигнал.
|
|
|
Подробное описание методов вы найдете в указанной ниже литературе. В данной работе для выполнения расчетов достаточно знания классического метода.
А. Переходный процесс при подключении последовательной RС -цепи к источнику постоянной ЭДС.
Дифференциальное уравнение, описывающее переходный процесс в рассматриваемой цепи, имеет вид
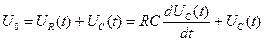. (1)
Решение дифференциального уравнения (1) в общем виде имеет вид
,
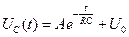при нулевых начальных условиях получаем, что
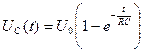, (2)
где RС = τ – постоянная времени цепи.
Зная выражение UC (t), можно определить ток переходного процесса:
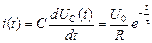. (3)
Напряжение на сопротивлении R определяется как
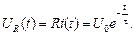(4)
Б. Переходный процесс при подключении последовательной RL - цепи к источнику постоянной ЭДС.
Дифференциальное уравнение, описывающее переходный процесс в рассматриваемой цепи, имеет вид
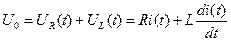. (5)
Решение этого уравнения при нулевых начальных условиях есть
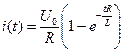, (6)
где L / R = τ – постоянная времени цепи.
Зная выражение i (t), можно определить UR (t) и UC (t):
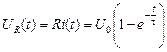, (7)
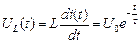. (8)
В. Переходный процесс при подключении последовательной RLC - цепи к источнику постоянной ЭДС.
Дифференциальное уравнение, описывающее переходный процесс в рассматриваемой цепи, имеет вид
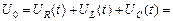
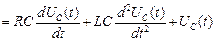. (9)
В связи с тем, что корни характеристического уравнения
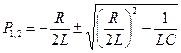
могут быть действительными или комплексными, решение дифференциального уравнения может иметь апериодический или колебательный характер.
В1. Апериодический режим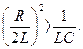 
Решение дифференциального уравнения (9) в общем виде имеет вид
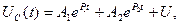(10)
где Р 1, Р 2 < 0.
Постоянные А 1 и А 2 определяются из начальных условий
|
|
|
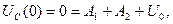
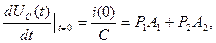
т.е.
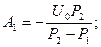
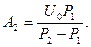
Переходное напряжение на емкости равно
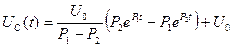. (11)
Величины тока и напряжений переходного процесса определяются выражениями (3), (4), (8) соответственно:
;
;
.
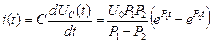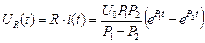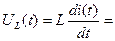
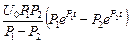В2. Колебательный режим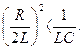 
Решение дифференциального уравнения (9), как и в предыдущем случае, описывается выражением (11), где
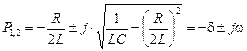– комплексно сопряженные величины;
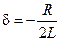– коэффициент затухания;
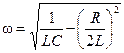– угловая частота колебаний.
Обозначив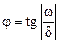 
, выражение (11) представим в виде
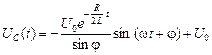. (12)
Переходные величины тока, напряжений на резисторе и емкости определяются формулами (3), (4) и (8) соответственно:
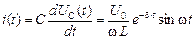, (13)
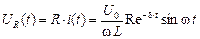, (14)
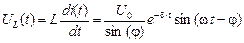. (15)
Переходный процесс носит колебательный характер с затуханием. Скорость затухания определяется коэффициентом затухания δ.
Отношение двух последующих амплитуд одного знака называется декрементом затухания Δ:
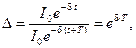
здесь 
– период колебаний.
Логарифмический декремент затухания ln Δ = ξ = δ Т.
Рабочее задание
1. На макете, схема которого показана на рис.1, путем переключений найдите способы получения последовательных RС -, RL - и RLС -цепей. Для изучения переходных процессов для всех трех вариантов подайте на вход цепи от генератора прямоугольный сигнал, установив его параметры по указанию преподавателя.
 |
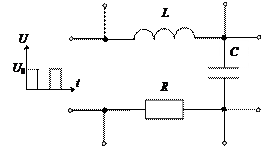Рис. 1
2. С помощью осциллографа убедитесь, что параметры подаваемого на вход цепи прямоугольного сигнала соответствуют указанным значениям. Наблюдение проведите, установив предварительно сопротивление R, равным 1кОм
3. Исследуйте переходный процесс в RС -цепи, установив R в пределах 5 – 8 кОм. Зарисуйте кривые переходных процессов на элементах R и С с указанием масштаба времени. Пользуясь изображением переходного процесса, определите численное значение постоянной времени цепи τ.
4. Рассчитайте численное значение τ по данным R и С. Сравните расчетные и экспериментальные данные.
5. Исследуйте переходный процесс в RL -цепи, установив R в пределах 500 – 1500 Ом. Зарисуйте кривые переходных процессов на элементах R и L с указанием масштаба времени. Пользуясь изображением переходного процесса, определите численное значение постоянной времени цепи τ.
6. По данным R и τ рассчитайте численное значение индуктивности L.
7. Исследуйте переходный процесс в RLС- цепи, выбрав R так, чтобы реализовать колебательный режим. Зарисуйте кривую переходного процесса с указанием масштаба времени. Пользуясь изображением переходного процесса, определите период колебаний τ и отношение амплитуд через период А 1 / А 2.
|
|
|
8. Для RLС -цепи выберите R так, чтобы реализовать критический режим (режим, при котором колебания прекращаются). Зарисуйте кривую переходного процесса с указанием масштаба времени.
Зафиксируйте значения R для указанных режимов.
9. Рассчитайте вид зависимости UR (t) в переходном процессе для всех трех исследуемых цепей.
10. Покажите, что
ξ – логарифмический декремент затухания;
R K – активная составляющая сопротивления катушки;
R ПЛ – полное активное сопротивление цепи (R ПЛ = R + R K);
L – индуктивность катушки;
R КР – критическое сопротивление цепи могут быть выражены через измеренные величины Т и А 1/ А 2 формулами
.
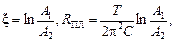
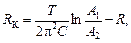
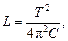
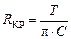11. Пользуясь формулами п.10, рассчитайте численные значения ξ, R K, R ПЛ, L, R КР.
12. По результатам экспериментальных и теоретических исследований сформулируйте выводы о влиянии параметров элементов рассмотренных цепей на характер получаемых переходных процессов.
Контрольные вопросы
1. Что такое переходный процесс?
2. Какова физическая сущность переходных процессов в электрических цепях?
3. Как формулируются законы коммутации? Каков физический смысл законов коммутации?
4. Какие Вам известны методы расчета переходных процессов?
5. Каков смысл принужденной и свободной составляющих переходных токов и напряжений?
6. Что такое постоянная времени цепи? Как определяется постоянная времени – расчетно и экспериментально?
7. Каково практическое значение переходных процессов?
Лабораторная работа N7
|
|
|
