 |
Краткие теоретические сведения
|
|
|
|
Под резонансным режимом работы электрических цепей с элементами R,L,C понимают такой режим, при котором эквивалентное сопротивление цепи является чисто активным (ток и напряжение на входе цепи совпадают по фазе). Отсюда следует, что для определения условий наступления резонанса надо приравнять нулю мнимую часть комплекса входного сопротивления или проводимости цепи.
Если в резонансе находится цель, содержащая последовательно соединенные участки, имеющие индуктивный и емкостной характер, режим называется резонансом напряжений. Если в резонансе находится разветвленная цепь, содержащая параллельно соединенные участки, имеющие индуктивный и емкостной характер, режим называется резонансом токов.
Резонанс напряжений
Рассмотрим резонанс напряжений в последовательном контуре (рис. 1).

Рис. 1
Комплексное сопротивление цепи равно
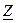 = R + j (ω L – 1/ω С). (1)
= R + j (ω L – 1/ω С). (1)
Условие резонансного режима для рассматриваемой цели следующее:
ω L – 1/ω C = 0; ω L = 1/ω C. (2)
Из (2) следует, что резонанса можно достигнуть, изменяя либо частоту источника, либо параметры цепи – L или С.
Угловая частота ω0, при которой наступает резонанс, называется резонансной частотой и из (2) определяется как
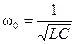 .
.
Индуктивное или емкостное сопротивление при резонансе называется характеристическим сопротивлением ρ:
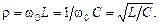 (3)
(3)
Векторная диаграмма токов и напряжений при резонансе представлена на рис. 2.
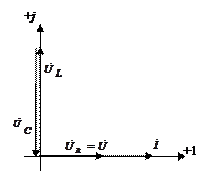 |
Рис. 2
Отношение напряжения на индуктивности или емкости к приложенному к цепи при резонансе называется добротностью контура Q.
Q = 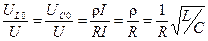 . (4)
. (4)
Добротность показывает, во сколько раз напряжение на индуктивности (или на емкости) превышает напряжение на входе схемы в резонансном режиме.
|
|
|
Величина, обратная добротности, называется затуханием контура
d = 1/ Q. (5)
Добротности контуров, используемых при высоких частотах, могут достигать 50 – 300. Из уравнения (4) следует, что при резонансе UL = UC = QU, т.е. напряжение на емкости и индуктивности может в десятки и сотни раз превышать напряжение, приложенное ко всему контуру. Это свойство последовательного контура и послужило основанием для наименования режима резонансом напряжений.
Рассмотрим частотные характеристики последовательного контура, т. е. зависимость I, UL, UC, угла сдвига фаз (φ) между напряжением и током от частоты приложенного напряжения. Значение тока в цепи (рис.1) равно
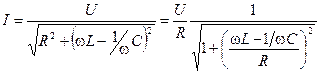 . (6)
. (6)
Из формулы (6) ясно, что максимального значения I 0 ток достигнет при частоте, равной резонансной. При этом 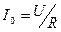 . Чем меньше R (при неизменных L и С), т. е. чем больше добротность контура Q, тем более острой становится форма кривой I = I (ω) на рис. 3, на котором построены амплитудно-частотные характеристики последовательного контура.
. Чем меньше R (при неизменных L и С), т. е. чем больше добротность контура Q, тем более острой становится форма кривой I = I (ω) на рис. 3, на котором построены амплитудно-частотные характеристики последовательного контура.
Качественно оценим изменения напряжений на емкости и индуктивности. При частоте, равной нулю, сопротивление конденсатора бесконечно велико, и приложенное ко всей цепи напряжение окажется на зажимах конденсатора. При этом сопротивление катушки и напряжение на ней равны нулю.
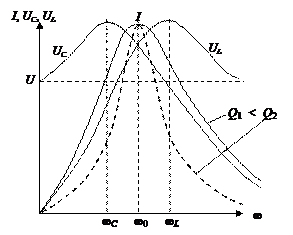 |
Рис. 3
Наоборот, при бесконечно большой частоте катушка представляет собой разрыв (ω L→∞), и напряжение на ее зажимах равно приложенному к цепи напряжению, а напряжение на конденсаторе равно нулю (1 / ω С = 0). При резонансной частоте напряжения на индуктивности и емкости равны между собой. Максимального значения UC достигает при ω C < ω0, а UL –при ω L > ω0.
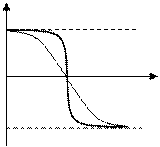
На рисунке 4 представлена фазочастотная характеристика, т. е. φ= φ(ω). Эту характеристику строят исходя из равенства
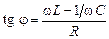 . (7)
. (7)
|
|
|
При ω= 0 угол φ = – π/2, а при ω = ω0 φ = 0; при ω → ∞ φ = π/2.
Таким образом, при частотах ниже резонансной сопротивление контура носит емкостной характер, при частоте больше резонансной – индуктивный.
Из уравнения (7) следует: чем меньше R (при неизменных L и С), т.е. чем больше добротность контура Q, тем более резко изменяется кривая φ = φ(ω) между своими предельными значениями (–π/2) и (π/2) (рис. 4).
|
 |
|
|
|
|
|
|
|
Рис. 4
Установим связь между полосой пропускания последовательного контура и его добротностью.
Полосой пропускания контура условились называть такой диапазон частот, в пределах которого активная мощность Р контура составляет не менее половины активной мощности Р 0, которую контур поглощает при резонансной частоте.
Следовательно, на границах полосы пропускания контура
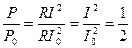 или
или 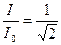 .
.
Напомним, что 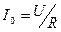 – ток при резонансе. Зависимость
– ток при резонансе. Зависимость 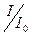 от частоты легко получить из уравнения (6):
от частоты легко получить из уравнения (6):
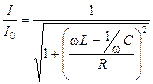 . (8)
. (8)
График зависимости 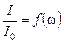 показан на рис. 5.
показан на рис. 5.
 |
Рис. 5
Величина 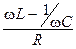 в уравнении (8) носит название обобщенной расстройки. На границах полосы пропускания
в уравнении (8) носит название обобщенной расстройки. На границах полосы пропускания

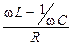 = 1.
= 1.
Практический интерес представляют контуры, для которых Δω = ω – ω0 существенно меньше ω0. В этом случае связь между Q, ω и ω0 легко получить, преобразовывая соотношение
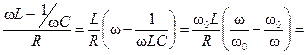
=Q 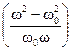 = Q
= Q 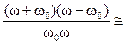 2 Q
2 Q 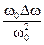 = 2 Q
= 2 Q 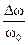 . (9)
. (9)

Так как на границах полосы пропускания 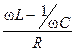 =1, то из уравнения (9) следует
=1, то из уравнения (9) следует 
Q = 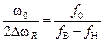 , (10)
, (10)
и ширина резонансной кривой δ = f 0 /Q, где 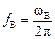 и
и 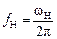 – соответственно верхняя и нижняя граничные частоты полосы пропускания (рис. 5);
– соответственно верхняя и нижняя граничные частоты полосы пропускания (рис. 5); 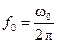 – резонансная частота контура.
– резонансная частота контура.
Резонанс токов
Рассмотрим резонанс токов в цепи, называемой параллельным колебательным контуром (рис. 6).
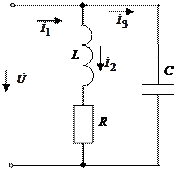 |
Рис. 6
Комплексная проводимость такой цепи равна
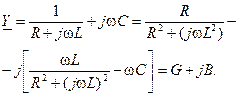 (11)
(11)
Условие резонансного режима для рассматриваемой цепи
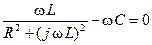 (12)
(12)
приводит к следующему соотношению для резонансной частоты:
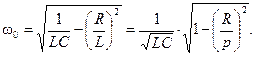 (13)
(13)
При 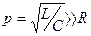 резонансная частота (13) совпадает по величине с резонансной частотой для последовательного контура
резонансная частота (13) совпадает по величине с резонансной частотой для последовательного контура 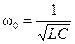 .
.
Векторная диаграмма для резонансного режима параллельного контура с учетом R представлена на рис. 7.
В случае резонанса реактивные составляющие токов в параллельных ветвях равны по величине и противоположны по фазе:
|
|
|
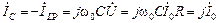 Q. (14)
Q. (14)
Таким образом, при резонансе токи в параллельных ветвях в Q раз превосходят ток I 0в неразветвленной части цепи.
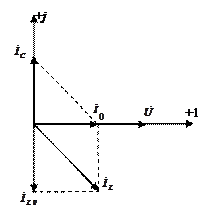 |
Рис. 7
Рассмотрим амплитудно-частотные характеристики параллельного резонансного контура. В предположении, что R= 0, 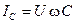 ,
, 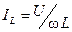 ,
, 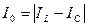 . На рисунке 8 представлена зависимость этих величин от частоты.
. На рисунке 8 представлена зависимость этих величин от частоты.
 |
Рис. 8
На рисунке 9 приведена фазочастотная характеристика параллельного контура. Она строится согласно уравнению 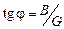 (см. соотношение (11)). При ω < ω0 сопротивление контура имеет индуктивный характер, при ω > ω0 – емкостной.
(см. соотношение (11)). При ω < ω0 сопротивление контура имеет индуктивный характер, при ω > ω0 – емкостной.
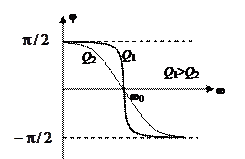 |
Рис. 9
Рабочее задание
Исследуйте резонансный контур (рис.10) экспериментально.
1. Выполните измерения, необходимые для построения резонансных кривых (амплитудно-частотных характеристик), выражающих зависимость напряжения на элементах контура R, L, С от частоты подаваемого от генератора на вход цепи переменного напряжения.
 |
Рис. 10
2. По данным измерений постройте резонансные кривые 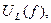
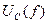 в общих осях, кривую
в общих осях, кривую 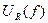 – отдельно.
– отдельно.
3. По данным эксперимента, пользуясь характеристикой 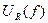 , определите численные значения
, определите численные значения
f 0– резонансной частоты;
U 0 R –напряжения на резисторе R при резонансе;
δ – ширины резонансной кривой.
Пользуясь характеристикой 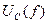 , определите значение максимума функции U 0 C.
, определите значение максимума функции U 0 C.
По формулам Q = U 0 C. / U BXи δ1 = ω0/ Q  рассчитайте численное значение добротности контура и ширины резонансной кривой.
рассчитайте численное значение добротности контура и ширины резонансной кривой.
4. Покажите, что для данного контура
R К – активная составляющая сопротивления катушки индуктивности;
R ПЛ – полное активное сопротивление контура (R ПЛ = R + R K)
L – индуктивность катушки;
С – емкость конденсатора;
ρ – характеристическое сопротивление контура
могут быть определены через измеренные величины по следующим формулам:
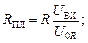
 ;
; 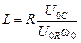 ;
;
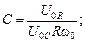
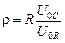 .
.
5. Рассчитайте численные значения величин R ПЛ, R K, L, C, ρ по приведенным в п. 4 формулам.
Контрольные вопросы
|
|
|
1. Что понимают под резонансным режимом работы электрической цепи?
2. В чем проявляется резонанс напряжений?
3. Каковы условия возникновения резонанса напряжений и способы его достижения?
4. Каков физический смысл добротности контура?
5. Как в общем случае для любого резонансного контура рассчитать его резонансную частоту и добротность?
6. Каково практическое применение явления резонанса?
7. Почему при резонансе напряжений ток максимален?
8. В какой цепи и при каких условиях возможен резонанс токов?
9. Почему при резонансе токов ток минимален?
Лаборатоная работа N5
|
|
|


