 |
Краткие теоретические сведения
|
|
|
|
Любая электрическая цепь состоит из реальных элементов, большинство которых являются нелинейными. Нелинейным называется элемент, вольтамперная характеристика (ВАХ) которого является нелинейной, т.е. зависимость тока от напряжения описывается уравнением второго или более высокого порядка.
Нелинейная электрическая цепь аналогично линейной электрической цепи описывается уравнениями равновесия на основе законов Кирхгофа. Полученная система состоит как из линейных, так и из нелинейных уравнений. Аналитически решить такую систему уравнений можно только в исключительных случаях. Чаще всего эти уравнения решаются численными методами при помощи ЭВМ, графоаналитическими или графическими методами.
В любом случае анализ электрической цепи возможен только тогда, когда задана ВАХ нелинейного элемента. ВАХ может задаваться аналитическим выражением, что бывает крайне редко, а чаще – в виде таблицы или графика. Кроме того, в сложной разветвленной электрической цепи можно проводить различные эквивалентные преобразования, которые приводят к упрощению цепи. Например, параллельное соединение элементов можно заменить эквивалентным элементом, ВАХ которого получается суммированием значений тока исходных элементов при одном и том же напряжении, а последовательное соединение элементов можно заменить эквивалентным, ВАХ которого получается путем сложения напряжений при одном и том же токе.
Рассмотрим наиболее распространенный графический метод анализа электрической цепи с нелинейным элементом, где рабочий режим нелинейного элемента можно определить как точку пересечения нагрузочной прямой с графиком ВАХ.
|
|
|
а) б)
Рис. 1
Определим в цепи рис. 1а ток I и напряжение U НЭ на нелинейном элементе. При этом известны Е, R и задана графически (рис. 1б) ВАХ нелинейного элемента. В данном случае задача сводится к нахождению на ВАХ рабочей точки А, по которой определяются ток в цепи и напряжение на нелинейном элементе.
Данная цепь описывается уравнением равновесия
R · I + U НЭ = Е, (1)
из которого определяется зависимость 
:
. (2)
Уравнение (2) соответствует прямой, которая пересекает оси координат в точках (0, Е / R) и (Е,0). Таким образом, I и U НЭ связаны между собой двумя соотношениями: одно выражено нелинейной ВАХ графически, другое – уравнением (2), определяющим так называемую нагрузочную прямую. Тогда очевидно, что пересечение ВАХ с нагрузочной прямой определит рабочую точку, т.е. искомый режим нелинейного элемента.
Отметим, что рассмотренный метод относится к случаю последовательного соединения трех элементов: Е, R и нелинейного элемента. Однако случай сложной цепи, содержащей нелинейный элемент, может быть сведен к рассмотренному путем преобразования цепи по методу эквивалентного генератора. При этом очевидно, что точки пересечения нагрузочной прямой с осями координат ВАХ определяются напряжением холостого хода и тока короткого замыкания между узлами, к которым присоединен нелинейный элемент.
Важной характеристикой нелинейного элемента является величина его дифференциального сопротивления. Оно определяется соотношением
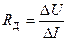. (3)
 |
Рис. 2
Существенно, что R Д может быть, в частности, величиной отрицательной (рис. 2, точка C), равной нулю (точка D) или бесконечности (точка А). Это определяет свойства нелинейного элемента и дает возможность в данном случае, например, использовать его для усиления сигналов (точка C) или для стабилизации (точки А и D).
Вводится также понятие статического сопротивления, определяемого отношением
|
|
|
, (4)
которое всегда положительно.
При наличии в цепи источников ЭДС постоянной и переменой величин (например, гармонического воздействия) анализ нелинейной цепи возможен методом замены нелинейного элемента линейной схемой замещения, что приводит к линеаризации всей цепи. Положим, что в рабочем режиме цепи с нелинейным элементом изменение напряжения на нелинейном элементе относительно невелико так, что в пределах Δ U участок ВАХ с определенным приближением можно заменить прямой, касательной к ВАХ в рабочей точке А (рис. 3).
Рис. 3
Тогда уравнение касательной, замещающей ВАХ в окрестностях рабочей точки, запишется как
, (5)
где R Д – дифференциальное сопротивление нелинейного элемента в данной точке А.
 |
Рис. 4
Уравнению (5) можно поставить в соответствие два последовательно соединенных элемента Е 0 и R Д, которые составят схему замещения данного нелинейного элемента (рис. 4).
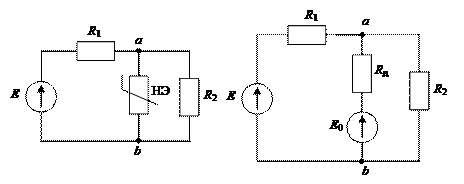Так, например, в схеме стабилизации напряжения на нагрузке R 2 (рис. 5а) анализ условий, определяющих возможность стабилизации, удобно проводить с использованием линейной схемы замещения (рис. 5б).
а) б)
Рис. 5
В соответствии со схемой замещения стабилизируемое напряжение
(6)
или для приращений
. (7)
Идеальная стабилизация достигается при условии 
при Δ Е ≠ 0, что выполняется, очевидно, при R Д = 0.
Заметим, что в принятых обозначениях коэффициент стабилизации определяется отношением
. (8)
Рабочее задание
1. Экспериментально определите зависимость величины стабилизируемого напряжения Uab от величины напряжения источника питания Е; при этом источник е (t) отключен, и ток в ветви
Рис. 6
с элементами R 3, С равен нулю. Схема макета представлена на рис. 6.
Диапазон возможного изменения Е выберите по согласованию с преподавателем. Данные представьте в виде таблицы.
2. По данным п. 1 постройте график зависимости напряжения Uab от Е.
3. В соответствии с графиком п. 2 определите рабочий диапазон возможного изменения величины Е в пределах участка стабилизации (участок кривой, близкий к горизонтальному). Определите на этом участке приращения соответствующих напряжений на участке стабилизации.
|
|
|
4. По данным п. 3, пользуясь формулой
= 
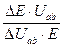, (9)
рассчитайте коэффициент стабилизации напряжения.
5. Снимите ВАХ стабилитрона I ст = f (U СТ). Для этого, изменяя Е от Е MAX до нуля, при каждом значении Е фиксируйте напряжение на стабилитроне U CT и на сопротивлении R 1. Ток через стабилитрон определите по формуле 
. При этом имеется в виду, что токи через R 1 и стабилитрон практически одинаковы, так как в области стабилизации R CT << R 2. Представьте данные п. 5 в виде таблицы.
6. По данным п. 5 постройте ВАХ стабилитрона в третьем квадранте системы координат.
7. Для рабочего значения Е постройте на графике ВАХ нагрузочную прямую. Поскольку R 2 >> R 1, за напряжение холостого xода между точками а и в можно принять рабочее значение Е. Зафиксируйте координаты рабочей точки U CT, I CT.
8. Для полученной в п.7 рабочей точки рассчитайте по ВАХ стабилитрона численные значения параметров элементов его схемы замещения:
R Д – дифференциального сопротивления;
Е 0 – ЭДС источника.
9. Определите статическое сопротивление стабилитрона R CT в рабочей точке и величину мощности P CT, рассеиваемую на стабилитроне.
10. Зарисуйте исследуемую схему, заменив в ней стабилитрон его линейной схемой замещения. Пользуясь методом двух узлов, выразите напряжение Uab через параметры элементов Е, R 1, R Д, E 0. Докажите, что коэффициент стабилизации для данной цепи может быть выражен формулой
. (10)
11. Подключите к макету дополнительно источник гармонического напряжения e (t). Установите его частоту равной 1 кГц и выходное напряжение – 1В. Измерьте переменное напряжение Uab.
12. Пользуясь схемой замещения (п.10), рассчитайте переменную составляющую напряжения Uab, создаваемую источником е (t). При расчете учтите, что ХC >> R 3 и R Д << R 2. Сравните расчетные данные с измерениями (п. 11).
13. Полученные в работе данные Е, Uab, σ, I СТ, R Д, Е 0, R CT, Р CT, σ2 сведите в общую таблицу.
Контрольные вопросы
1. Какие нелинейные элементы Вам известны, и для чего они применяются?
2. Какие методы расчета нелинейных цепей Вам известны?
3. Что такое нагрузочная прямая, и как она строится?
|
|
|
4. Как определяется линейная схема замещения нелинейного элемента? При каких условиях линейная схема замещения нелинейного элемента достаточно точно воспроизводит его свойства?
5. Как определить для нелинейного элемента его статическое и дифференциальное сопротивления?
6. Каково назначение стабилизатора напряжения?
Сводная таблица данных
| Определяемая величина | Численное значение |
| σ (экспер.) | |
| R Д | |
| Е 0 | |
| R СТ | |
| σ (расчет.) |
ЛИТЕРАТУРА
1. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи: Учебник. –10-у изд. – М.: Гардарики, 2001. – 638 с.
2. Курс электротехники: Учеб. для вузов/А.С. Касаткин, М.В. Немцов.- 10-е изд., стер.- М.:Высш.шк.,2009.-542 с.: ил.
3. Электротехника: Учебное пособие /И.И. Иванов, Г.И. Соловьев. - 6-е изд., стер. – СПб.: Издательство «Лань», 2009. – 496 с.: ил. – (Учебники для вузов. Специальная литература
4. Электротехника и электроника: Учебник/ О.П. Новожилов. – М.: Гардарики, 2008. – 653 с.
5. Электротехника и электроника: Курс лекций/ Г.В. Савилов. – М.: Издательско-торговая корпорация «Дашков и Кº», 2009. – 324 с.: ил.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ.. 3
Лабораторная работа № 1. ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ ПОСТОЯННОГО ТОКА 4
Лабораторная работа N2. ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ ПЕРЕМЕННОГО ТОКА 13
Лабораторная работа № 3. ИССЛЕДОВАНИЕ ТРЕХФАЗНОЙ ЦЕПИ ПРИ СОЕДИНЕНИИ НАГРУЗКИ «ЗВЕЗДОЙ» 23
Лабораторная работа № 4. РЕЗОНАНС НАПРЯЖЕНИЙ.. 25
Лаборатоная работа N5. ЧЕТЫРЁХПОЛЮСНИК ПЕРЕМЕННОГО ТОКА 25
Лабораторная работа N6. ПЕРЕХОДНЫЕ ПРОЦЕССЫ... 25
Лабораторная работа N7. ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ С НЕЛИНЕЙНЫМ ЭЛЕМЕНТОМ 25
ЛИТЕРАТУРА.. 25
Редактор З.И.Сныкова
Компьютерная верстка
ЛР №020713 от 27.04.1998
Подписано к печати.. 2012 Формат бумаги 60х84.16
Печать ризограф. Бумага МВ Печ.л. 5
Заказ Тираж 100 экз. Цена договорная
Отдел множительной техники ИАТЭ
249035, г.Обнинск, Студгородок, 1
|
|
|
