 |
Краткие теоретические сведения
|
|
|
|
Особенность прохождения гармонического тока через реактивные элементы цепи – емкостные и индуктивные сопротивления связана со смещением в этих элементах фаз токов относительно напряжений. Это приводит к необходимости характеризовать токи и напряжения не только их численным значением, но и фазой (углом) относительно некоторого выбранного уровня отсчета. Мгновенное значение гармонического тока (напряжения) можно выразить тригонометрической функцией
i = Im sin (ω t + φ). (1)
При этом в процессе расчета цепей приходится производить действия с тригонометрическими функциями разных аргументов (фаз), что приводит к громоздким вычислениям. Обычно расчет цепей гармонического тока производится так называемым символическим методом с применением комплексных величин. Суть его заключается в следующем.
Теория показывает, что гармоническая функция (1) может быть отображена комплексной функцией
. (2)
Благодаря этому операция с тригонометрическими функциями заменяется более простой и наглядной операцией с комплексными числами. Кроме того, оперируют не с мгновенными значениями, а с амплитудными комплексными значениями, для чего временной член в выражении (2) отбрасывают. Выражение комплексной амплитуды
содержит в себе информацию о том, какая величина амплитуды колебаний тока (Im – модуль комплекса) и каково смещение данного колебания по фазе относительно выбранного уровня (φ – аргумент комплекса).
На практике величину переменного тока и напряжения характеризуют действующим значением. Оно определяется как среднеквадратичное мгновенного значения за период. Для гармонического тока (напряжения) действующее значение I просто связано с амплитудным значением:
|
|
|
.
С токами и напряжениями, выраженными комплексно, в процессе расчета производятся обычные математические действия. При этом, где это необходимо, по формуле Эйлера от показательной формы комплексного числа переходят к его алгебраической форме:
. (3)
Здесь I а – действительная, jI P – мнимая части комплексного числа, записанного в алгебраической форме,
Переход от алгебраической формы комплекса к показательной осуществляется по формулам
, 
.
Отметим, что каждому комплексному числу можно поставить в соответствие вектор на комплексной плоскости. На рисунке 1 иллюстрируется связь параметров комплекса (3) с координатами вектора. Знаками ±1 отмечена ось действительных значений комплекса, ± j – мнимых значений. Положительный отсчет угла ведется против часовой стрелки.
 |
Рис.1
Отображение комплекса векторами дает возможность наглядно представить токи и напряжения данной цепи совокупностью векторов, что дает ее векторную диаграмму.
Символический метод требует выражения сопротивления цепи также в виде комплексов. Определим их.
Как известно, в общем случае ток и напряжение на элементах цепи R, L, С связаны следующими соотношениями:
; 
; 
.
Перейдем в этих выражениях к комплексным значениям. Для этого мгновенное значение тока i заменим на комплекс 
. В результате получим
(4)
В выражениях (4) величины
, 
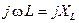представляют собой запись индуктивного и емкостного сопротивлений в комплексной форме. Их особенность, в отличие от активного сопротивления R, связана с зависимостью от частоты. Наличие множителя + j или – j определяет их действие, вызывающее смещение фазы тока относительно напряжения на +90º или –90º соответственно.
Расчет линейных цепей гармонического тока основывается на законах Кирхгофа в комплексной форме и при этом остаются применимы все те методы, которые применяются для расчета цепей постоянного тока (метод контурных токов, узловых потенциалов и др.).
|
|
|
Потребляемая цепью гармонического тока полная мощность складывается из двух составляющих:
P = UI cos φ – активной мощности;
Q = UI sin φ – реактивной мощности
(φ – угол сдвига фаз между напряжением и током).
Активная мощность потребляется активными элементами, преобразующими её в другие виды энергии (тепловую, механическую, световую и др.). Реактивная мощность потребляется реактивными элементами L и С и идет на создание магнитного и электрического полей. Существенное отличие реактивной мощности от активной в том, что её среднее значение за период равно нулю. Причем потребление реактивной мощности чередуется с её возвратом через каждые четверть периода.
Вводится также понятие полной мощности
Размерность полной, активной и реактивной мощностей одинакова, однако для них вводятся разные наименования: для полной мощности – вольтампер (ВА), для активной – ватт (Вт), для реактивной – вольтампер реактивный (ВАр).
Ниже мы приводим пример расчета цепи гармонического тока. Для электрической цепи, схема которой показана на рис. 2, определим токи в ветвях, напряжения на элементах, мощность, потребляемую цепью. Построим векторную диаграмму.
 |
Рис. 2
Дано: R = 100 Ом, ХL = 30 Ом, XC = 40 Ом, Е = 100 В.
Для определения токов воспользуемся методом контурных токов.
Исходные уравнения:
.
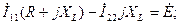
Откуда 
= 
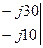= 1200– j 1000 = 156 
;
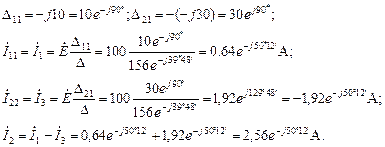
Определим напряжения на элементах:
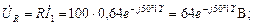
Определим мощности, потребляемые цепью:
Р = I 1· Е соs φ = 0,64 100 cos 50º12' = 40 Вт,
Q = I 1· Е sin φ = 0,64 100 siп 50º12' = 49,2 ВАр,
S = I 1· Е = 0,64·100 = 64 ВА.
По данным расчета строим векторную диаграмму (рис. 3).
Рис. 3
Рабочее задание
1. Для электрической цепи, схема которой приведена на
рис. 4, постройте векторную диаграмму токов 
и напряжений 
при условии равенства модулей всех сопротивлений R 1 = R 2 = R 3 = XC 1 = XC 2.
Примечание. Построение диаграммы начните с векторов 
, взяв их длины равными 4 см.
 |
Рис. 4
2. Включите на вход цепи (рис.4) генератор переменного напряжения, выбрав его частоту так, чтобы модуль реактивного сопротивления 
был равен величине активного сопротивления R.
|
|
|
3. Выполните следующие измерения:
а) всех напряжений и токов, указанных в п.1 (ток I 3 измеряется косвенным способом по данным напряжения на резисторе R 3);
б) фазовых углов напряжений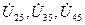 
относительно входного напряжения 
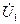(на рис.5 показано включение фазометра для измерения фазового угла напряжения 
).
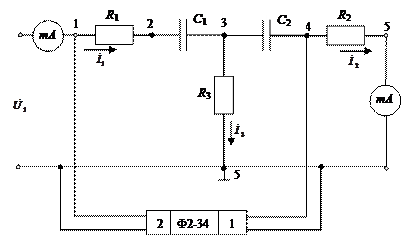
Рис. 5
4. По данным векторной диаграммы определите численные значения всех токов и напряжений, указанных в п.1, и их фазовые углы.
Примечание. За отсчетное значение напряжения примите величину U 1, за отсчетное значение тока – величину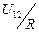 
.
5. Пользуясь данными измерений определите численные значения активной, реактивной и полной мощностей, потребляемых цепью. Необходимый для расчета фазовый угол определите из векторной диаграммы.
6. Пользуясь данными измерений и значением фазового угла, определенным в п.5, вычислите комплекс входного сопротивления цепи (активную и реактивную составляющие). Вычислите комплексное сопротивление цепи, используя параметры элементов цепи, указанные в макете. Сравните полученные результаты.
7. По данным измерений запишите мгновенные значения напряжений 
.
8. По заданным входному напряжению и параметрам элементов цепи рассчитайте комплексы токов и напряжений на элементах цепи (модули и аргументы).
Контрольные вопросы
1. Какими параметрами характеризуется синусоидальный ток. Что понимается под действующим значением тока?
2. В чем особенность прохождения синусоидального тока через элементы R, L, С? Почему при расчете синусоидальных токов применяются комплексные величины?
3 Какие существуют формы записи комплексных чисел?
4. Каков физический смысл активной и реактивной мощностей?
5. Что такое коэффициент мощности?
6. Как записываются выражения для индуктивного и емкостного сопротивлений в комплексной форме?
7. Как записывается формула комплексного сопротивления участка цепи при последовательном соединении элементов R, L, C.?
8. Какова методика расчета цепей синусоидального тока при смешанном соединении сопротивлений?
|
|
|
9. Как рассчитываются активная, реактивная, полная мощности? Каков их физический смысл?
Таблица сводных данных
| Определяемая величина | Диаграмма | Измерения | Расчет |
| U 1 | |||
| U 12 | |||
| U 23 | |||
| U 13 | |||
| U 34 | |||
| U 45 | |||
| U 35 | |||
| U 25 | |||
| I 1 | |||
| I 2 | |||
| I 3 | |||
| Р | |||
| Q | |||
| S | |||
| φ U 11 | |||
| φ U 12 | |||
| φ U 13 | |||
| φ U 25 | |||
| φ U 35 | |||
| φ U 45 |
Лабораторная работа № 3
|
|
|
