Удельные погонные параметры линий СВН

Удельные погонные параметры линий СВН

К удельным погонным параметрам линии относятся активное 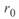 и реактивное  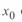сопротивления, а также активная  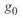и реактивная  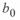поперечные проводимости на 1 км длины линии.

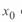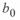Поскольку провода расщепленной фазы в расчетах могут быть заменены одним эквивалентным проводом, то значения  и  могут быть определены по тем же выражениям, что и для линий с одиночными проводами, но при замене радиуса одиночного провода радиусом эквивалентного провода .

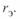Параметры 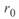 и 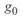 не зависят от геометрических параметров линии, но связаны с конструкцией фазы. Значение  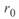определяется количеством проводов в фазе, а значение  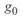— потерями активной мощности на корону, зависящими от конструкции фазы, и на утечки по изоляторам. Однако последние очень малы, и в расчетах их обычно не учитывают.

В расчетах значения 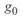 определяется только потерями на корону. При этом значение этих потерь зависит от погодных условий, для которых проводится расчет. В проектных расчетах следует принимать среднегодовые потери активной мощности на корону  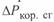при номинальном напряжении.

Удельные погонные параметры линии СВН рассчитываются по следующим выражениям:

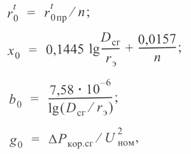                         (2. 19)

где 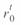 и 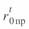 удельное погонное активное сопротивление фазы и провода соответственно при заданной температуре воздуха, Ом/км.

При расщеплении проводов (см. табл. 2. 1) существенно снижается значение 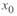 и возрастает значение  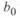по сравнению с аналогичными значениями для линии с одиночными проводами ( 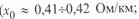; 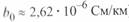). Это означает, что расщепление проводов приводит к увеличению пропускной способности линии и может рассматриваться в качестве одного из путей решения этой задачи. С другой стороны, увеличение значения  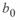ведет к увеличению зарядной мощности (реактивная мощность, определяемая емкостью линии) линии и, как следствие, к увеличению мощности компенсирующих устройств.

Активное сопротивление расщепленной фазы в 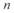 раз меньше сопротивления одиночного провода, что приводит к снижению потерь активной мощности на нагрев проводов.

 

Раздел 3. Основные характеристики некомпенсированной линии переменного тока

Тема 3. 1. Уравнения длинной линии

Под некомпенсированной линией без промежуточных отборов мощности понимается линия, не имеющая никаких компенсирующих устройств с сосредоточенными параметрами (реакторов, конденсаторных батарей и др. ), включенных последовательно или параллельно в каких-либо промежуточных точках на всем ее протяжении. В этом случае линия является однородной.

Передача электрической энергии по линии переменного тока осуществляется распространением вдоль нее электромагнитной волны, что создает электромагнитное поле линии. Это поле имеет две составляющие магнитное поле, обусловленное протеканием электрического тока в проводах, и электрическое поле, создаваемое напряжением между фазами линии и между каждой фазой и землей.

Поскольку ток и напряжение линии переменны, обе составляющих электромагнитного поля также изменяются во времени. Условное изображение магнитного и электрического полей приведено на рис. 3. 1.

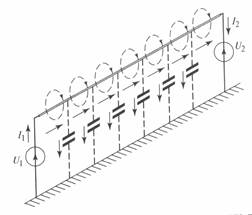
Рис. 3. 1. Условное изображение магнитного и электрического поля вдоль линии

 

Электрические параметры линии активное сопротивление проводов, индуктивность и емкость — равномерно распределены вдоль всей длины линии. Переменное напряжение, распределенное вдоль линии, приводит к появлению токов в емкостях между проводами и между проводами и землей. Емкостные токи, накладываясь на каждом элементарном участке линии на рабочий ток, определяемый передаваемой мощностью, вызывают непрерывное изменение суммарного тока по всей длине линии. В результате изменяются ЭДС самоиндукции и взаимоиндукции в проводах на каждом участке и значения напряжения вдоль линии. Все это приводит к достаточно сложным закономерностям изменения значений тока, напряжения и мощности вдоль линии.

Для определения этих закономерностей рассмотрим некоторый элементарный участок линии длиной 11, расположенный на расстоянии от начала линии (рис. 3. 2, а). В сложных электрических сетях с большим количеством узлов и источников питания понятия «начало» и «конец» линии определить трудно. В то же время для рассмотрения характеристик одиночной линии это необходимо знать. Поэтому условимся здесь и далее под началом линии понимать тот узел системы, от которого активная мощность направлена в линию, соответственно под концом узел системы, к которому активная мощность направлена с линии.

Схема замещения такого элементарного участка приведена на рис. 3. 2, б.

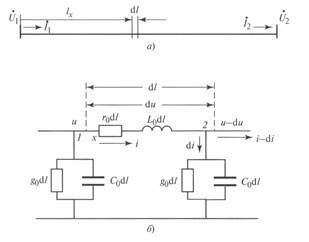
Рис. 3. 2. Элементарный участок линии (а) и схема его замещения (б)

 

Эта схема справедлива как для однофазной, так и для трехфазной линии. Для однофазной линии в качестве напряжения и тока должны рассматриваться их фазные значения, для трехфазной междуфазное напряжение и линейный ток.

При протекании тока i в продольной ветви схемы замещения выделенного участка напряжение в конце этого участка будет меньше, чем в его начале, на величину du за счет потери напряжения в активном сопротивлении и индуктивности на протяжении dl. Ток в продольной ветви следующего участка уменьшится на величину di за счет поперечной ветви рассматриваемого участка. Последний имеет две составляющие — ток в активной и ток в емкостной проводимости.

Изменения напряжения и тока на протяжении dl определяются уравнениями:

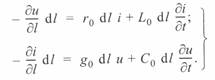              (3. 1)

Разделив оба уравнения на dl, получим

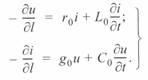                     (3. 2)

В уравнениях (3. 2) использованы мгновенные значения тока и напряжения линии, которые являются функциями двух переменных: времени и длины линии. Эти уравнения справедливы для любых изменений тока и напряжения во времени, т. е. для установившихся и переходных режимов.

При синусоидальном напряжении источника питания для установившегося режима в точке x можно записать:

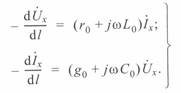                         (3. 3)

Здесь 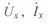 — действующие комплексные значения напряжения и тока в точке x;  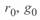— активные сопротивление и проводимость;  — индуктивность и емкость элементарного участка линии.

Длину элементарного участка удобно принять равной 1 км и в дальнейшем использовать удельные погонные параметры линии.

Обозначим удельное продольное сопротивление линии 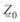 и удельную поперечную проводимость  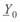как:

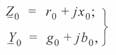                (3. 4)

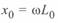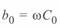где  и  — удельные погонные индуктивное сопротивление и емкостная проводимость линии соответственно;  активное сопротивление проводов; 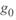 — проводимость с учетом потерь энергии на корону и утечек по изоляторам.

Уравнения (3. 3) при этом будут иметь вид:

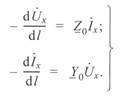             (3. 5)

Взяв первые производные от тока и напряжения по l, получим:

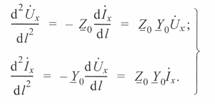              (3. 6)

Эти уравнения характеризуют изменения тока и напряжения вдоль линии.

Для напряжения и тока в некоторой точке x, отстоящей на расстоянии 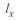 от начала линии, решения этих уравнений имеют следующий вид:

для напряжения

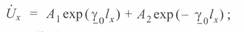                    (3. 7)

для тока с учетом (3. 5)

                        

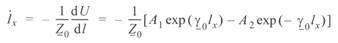
или

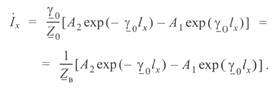                        (3. 8)

Здесь 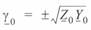 — корни характеристического уравнения системы (3. 6).

Отношение 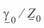 может быть представлено как

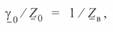
где 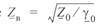 — волновое сопротивление линии.

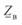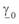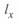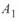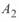Физический смысл  и  будет пояснен ниже. Переменной величиной здесь является  — текущая координата, постоянные интегрирования  и  определяются из начальных условий.

Ниже приводятся выражения для расчета параметров режима линии.

Расчет по данным начала линии. При или

                          (3. 9)

Решая систему этих уравнений, получаем:

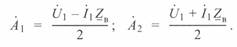
Подставляя значения 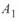 и  в (3. 7) и (3. 8) и учитывая, что

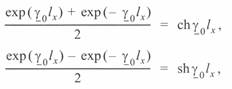
после преобразований получаем выражения для расчета параметров режима в промежуточной точке линии x:

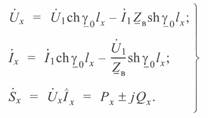                (3. 10)

Параметры режима конца линии при 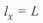 по данным ее начала определяются следующими уравнениями:

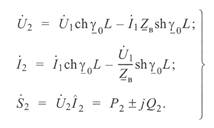              (3. 11)

где L — полная длина линии.

Расчет по данным конца линии. В качестве начальных условий могут быть приняты также параметры режима конца линии 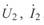 , где . В этом случае отсчет текущей координаты 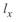 должен вестись в противоположном направлении, т. е. от конца линии.

Опуская промежуточные преобразования, для промежуточной точки x в этом случае можно записать:

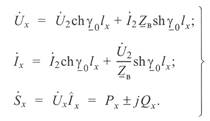                (3. 12)

Связь между параметрами режима начала линии по данным ее конца при 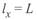определяется следующим образом:

 

 

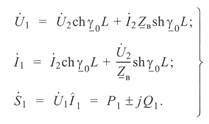                (3. 13)

Уравнения (3. 10)—(3. 13) справедливы как для однофазной линии, так и для трехфазной. Различие заключается лишь в том, что для однофазной линии в этих уравнениях используются значения фазного напряжения и тока. Кроме того, значения волнового сопротивления 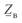 и коэффициента распространения электромагнитной волны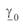

определяются с использованием иных значений удельных погонных параметров лини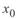и  и 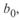, поскольку в однофазной линии отсутствуют взаимные индуктивность и емкость фаз.

При использовании уравнений (3. 10)—(3. 13) для трехфазной линии в них учитываются комплексные действующие значения междуфазного напряжения и линейного тока

В этом случае полная мощность трехфазной линии в промежуточной точке x определяется как

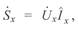            (3. 14)

где 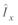  — сопряженное комплексное значение линейного тока.

При использовании фазного тока и междуфазного напряжения трёхфазной линии уравнения (3. 10) и (3. 12) для промежуточной точки примут вид:

по данным начала трехфазной линии

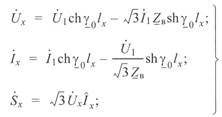            (3. 15)

по данным конца трех фазной линии

             (3. 16)

Приняв 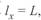, по (3. 15) и (3. 16) можно найти фазные токи, напряжения и мощности в начале и конце линии.

Полученные выше уравнения (3. 7) и (3. 8) дают основание рассматривать напряжение и ток в любой промежуточной точке линии как наложение двух волн (падающей и отраженной), двигающихся в противоположные стороны. Первый член правой части этих уравнений представляет собой падающую волну, второй — отраженную. Эта теория позволяет анализировать различные режимы линии, в том числе и переходные. Однако для решения практических инженерных задач обычно напряжение и ток рассматриваются как единые результирующие величины без разделения их на отдельные составляющие.

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: