 |
Тема 3.3. Уравнение идеализированной линии
|
|
|
|
Тема 3. 3. Уравнение идеализированной линии
При использовании расщепленных проводов для линий 330— 1150 кВ активное сопротивление фазы снижается пропорционально количеству проводов в ней, в то время как реактивное уменьшается в меньшей степени. Поэтому отношение 
возрастает по мере увеличения количества проводов фазы. Это соотношение для используемых марок проводов и стандартных конструкций фазы (см. табл. 3. 1) лежит в пределах 5, 5—24, 5, Иными словами, для линий СВН индуктивное сопротивление много больше активного 
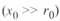, в особенности для линий 500 кВ и выше. Это еще одно отличие линий этих классов напряжений от линий 110—220 кВ, где в некоторых случаях эти сопротивления примерно равны или их ‚отношение имеет существенно меньшие значения.
Следует учесть и то обстоятельство, что значение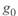 
определяется главным образом потерями мощности и энергии на корону. Однако потери на корону рассчитываются иными методами и учитываются в виде отбора мощности по концам линии. На параметры режима самой линии, в частности на экстремальные значения напряжения в некоторых режимах, эти потери практически не влияют. Поэтому для упрощенных расчетов режимов линии рассматриваемых классов напряжения можно пренебречь величинам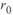и 
и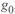 
, приняв 
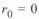и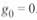 
. В этом случае коэффициент затухания 
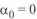, а выражения для коэффициента распространения волны и волнового сопротивления приобретают такой вид:
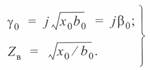(3. 21)
Это позволяет, в свою очередь, упростить уравнения длинной линии, исключив гиперболические функции комплексного переменного, вычисление которых вызывает определенные трудности, и заменить их тригонометрическими.
Рассмотрим преобразование гиперболических функций при принятых выше допущениях, имея в виду, что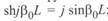 
; 
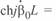
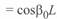, а также, что при 
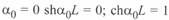. Отсюда будем иметь
|
|
|
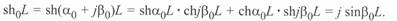
Аналогично
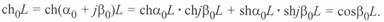
Тогда уравнения (3. 10)—(3. 13) применительно к идеализированной трехфазной линии могут быть записаны следующим образом. При заданных данных начала линии параметры режима в промежуточной точке линии будут определяться как
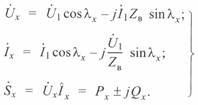(3. 22)
Здесь значение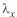 
отсчитывается от начала линии до точки x. Параметры режима конца линии по данным ее начала:
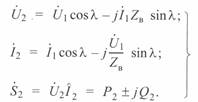(3. 23)
При заданных параметрах конца линии параметры режима в промежуточной точке линии будут определяться следующим образом:
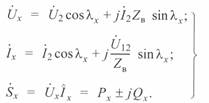(3. 24)
Здесь значение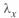 
отсчитывается от конца линии.
Параметры режима в начале линии по данным ее конца:
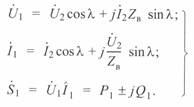(3. 25)
Для идеализированной линии активная мощность во всех точках одинакова:
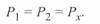(3. 26)
Напряжения и токи в промежуточных точках линии зависят от значения передаваемой активной мощности.
Тема 3. 4. Натуральная мощность линии
Одной из важных характеристик линии является ее натуральная мощность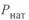 
. Рассмотрим это понятие несколько подробнее. Выделим элементарный участок трехфазной линии длиной 
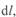, аналогичный рассматриваемому ранее, но не имеющий активного сопротивления 
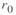и активной проводимости 
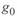(рис. 3. 3, а). Потери реактивной мощности в проводах линии на этом участке при некотором токе 
, протекающем по этому участку,
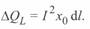
Генерация реактивной мощности участка
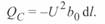
В этих выражениях ток — линейный, напряжение междуфазное. Суммарное значение реактивной мощности данного участка
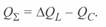(3. 27)
Зависимости этих составляющих от тока приведены на рис. 3. 3, 6. При некотором значении тока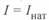 
сумма реактивных мощностей участка переходит через нуль и меняет знак. Это означает, что при данном значении тока на этом участке обеспечивается баланс реактивных мощностей, т. е. осуществляется взаимная компенсация реактивной мощности на каждом элементарном участке линии на всем ее протяжении. Такой режим называется режимом передачи натуральной мощности. Передаваемая активная мощность, соответствующая условию 
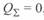, называется натуральной мощностью.
|
|
|
Ток, соответствующий этому режиму, может быть найден из (3. 27) при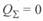 
:
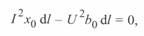
откуда
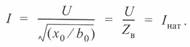(3. 28)
Этот ток, в данном случае линейный, называют натуральным током. Соответствующий ему фазный ток определяется как
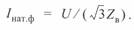
Помножив правую и левую части уравнения (3. 28) на U, получим мощность
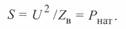(3. 29)
Отметим, что поскольку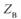 
в данном случае есть действительная величина, то I также действительная величина, совпадающая по фазе с напряжением U, а S это активная мощность.
Такой режим возникает при нагрузке линии на эквивалентное сопротивление нагрузки, равное волновому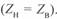 
. При этом, как известно, в линии отсутствуют отраженные волны.
Если принять напряжение в конце линии
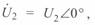
то ток в конце линии определяется как
а мощность в конце линии будет только активная:
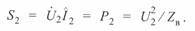
Для этого режима из (3. 24) найдем напряжение и ток в промежуточной точке:
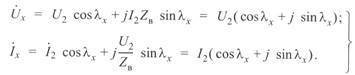(3. 30)
В этих уравнениях второй сомножитель правой части одинаков. Он представляет собой уравнение окружности единичного радиуса в комплексной плоскости. Это говорит о том, что в любой точке линии фазный сдвиг тока по отношению к напряжению в этой точке также одинаков и равен нулю, т. е. по линии без потерь передается только активная мощность, равная натуральной, а реактивная мощность во всех точках линии равна нулю.
Из этих уравнений следует также, что напряжение и ток в любой точке линии по модулю равны напряжению и току в конце линии. Они лишь сдвинуты по отношению к последним на некоторый угол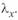 
.
Отсюда следуют два важных вывода:
1) при передаче по идеализированной линии активной мощности, равной натуральной, реактивная мощность в любой ее точке, включая начало и конец, равна нулю, поэтому потребность в каких-либо компенсирующих устройствах отсутствует;
2) напряжение и ток распределены вдоль линии равномерно, отсутствуют какие-либо превышения напряжения в промежуточных точках линии, требующие мероприятий по их снижению.
|
|
|
Отметим, что эти выводы в полной мере справедливы только для идеализированной линии*. При изменении значения напряжения U изменяется генерация реактивной мощности линии и, следовательно, изменяются условия баланса ее реактивных мощностей, который будет осуществляться при ином токе, т. е. при передаче иной активной мощности. Поэтому следует различать значения натуральной мощности для различных значений напряжения.
В расчетах могут быть использованы значения номинального напряжения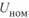 
, напряжения приемной системы 
, наибольшего расчетного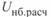 
или наибольшего рабочего напряжения 
. Для всех этих значений напряжения будут различны и значения натуральной мощности, например,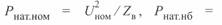 
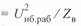и т. д.
Передаваемая по линии активная мощность является величиной непостоянной. Она изменяется во времени в соответствии с изменением нагрузки системы в достаточно широком диапазоне, который определяется ролью данной линии в системе. В любом случае передаваемая по линии мощность будет изменяться от некоторой минимальной до наибольшей. При этом будут нарушаться условия баланса реактивных мощностей линии.
При передаваемой мощности меньше натуральной ( 
), т. е. при 
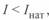, в линии возникает избыток реактивной мощности, который будет вызывать повышение напряжения в промежуточных точках линии и стекать с ее концов в прилегающие системы (узлы). Все это может привести к ряду нежелательных последствий и вынуждает принимать меры по ограничению стоков реактивной мощности и снижению напряжения в промежуточных точках линии. В качестве таких мер применяется установка реакторов, поглощающих избыточную реактивную мощность.
При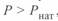 
, т. е. при 
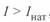, в линии возникает дефицит реактивной мощности, приводящий к понижению напряжения в ее промежуточных точках и узлах, к которым она подключена и в которых может потребоваться установка дополнительных источников реактивной мощности. Поскольку диапазон изменения передаваемой мощности достаточно широк, то для обеспечения баланса реактивных мощностей необходимо применять компенсирующие устройства различных типов.
|
|
|
Натуральная мощность характеризует пропускную способность линии. При средних значениях волнового сопротивления натуральная мощность для линий различного класса напряжения, определенная по номинальному напряжению, имеет следующие значения:
Разумеется, конкретная линия в зависимости от ее длины, конструкции и других факторов может иметь пропускную способность, отличающуюся от приведенных значений. Эти значения характеризуют лишь порядок величин.
При выводе уравнений длинной линии мы не задавались длиной последней. Поэтому эти уравнения справедливы для линий любой длины. Для относительно коротких линий, длина которых меньше длины электромагнитной волны, эти уравнения могут иметь другой вид. Например, если учесть, что при малых значениях аргумента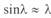 
и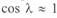 
, что справедливо для идеализированных линий 100—150 км, уравнения (3. 25) для случая связи параметров режима по концам линии будут иметь вид:
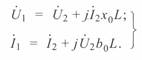(3. 31)
Таким образом, короткая линия является частным случаем длинной линии.
|
|
|
