Тема 3.6. Векторные и круговые диаграммы идеализированной линии

Тема 3. 6. Векторные и круговые диаграммы идеализированной линии

Векторные диаграммы линии длиной до 1500 км

 

Уравнения (3. 44) позволяют построить векторную диаграмму линии в комплексных координатах, представленную на рис. 3. 4. При построении диаграммы было принято .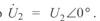

В этом случае все действительные величины расположены по действительной оси, в том числе и мощность 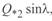, что соответствует положительному направлению реактивной мощности конца линии. Эта диаграмма справедлива при длине линии 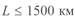. Из рис. 3. 4 следует:

Учитывая, что относительное значение активной мощности

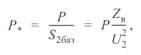
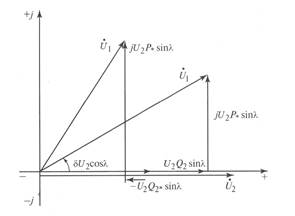
Рис. 3. 4. Векторная диаграмма идеализированной линии

 

после преобразований получаем

                 (3. 45)

где 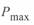 — максимальная мощность, которая может быть передана по линии и которая определяется ее электромагнитными свойствами.

Максимальная мощность

                                    (3. 46)

Отметим, что по линии переменного тока, для которой превалирующее значение имеет индуктивное сопротивление, активная мощность может быть передана при равных по модулю напряжениях 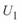 и 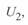, но это может быть осуществлено только при наличии фазового сдвига на угол  между этими напряжениями. При этом активная мощность передается от опережающего вектора к отстающему.

Если в (3. 46) принять 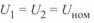 (при этом 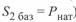) и разделить правую и левую части на  то в результате получим

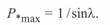                                     (3. 47)

Соответствующая зависимость приведена на рис. 3. 5. Значение 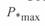 снижается по мере увеличения длины линии, и при 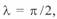, что соответствует 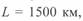, максимальная мощность равна единице, т. е. равна натуральной. При увеличении длины линии свыше 1500 км максимальная мощность вновь возрастает, однако, как это будет показано ниже, это увеличение сопровождается рядом отрицательных явлений, затрудняющих передачу мощности в диапазоне длин 1500—3000 км.

Рис. 3. 5. Зависимость максимальной 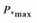  (кривая 1) и наибольшей передаваемой мощности  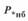(кривая 2) от длины линии 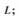; ограничение по нагреву проводов (кривая 3)

 

Как уже отмечалось в гл. 1, пропускная способность линии определяется рядом ограничений по отношению к 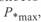, основными из которых являются ограничения по нагреву проводов и по устойчивости связываемых систем. Если учесть нормативный коэффициент запаса по статической апериодической устойчивости, равный 20 %, то зависимость наибольшей мощности 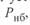, которую можно передать по линии с учетом этого коэффициента, пойдет несколько ниже.

Коэффициент запаса по устойчивости определяется как

                                     

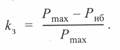
Отсюда наибольшая мощность, которую можно передать по линии по условию сохранения статической устойчивости связываемых систем

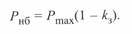
С учетом (3. 47) получим:

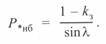                      (3. 48)

В то же время этой наибольшей мощности соответствует угол между напряжениями по концам линии  и :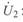

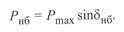
Отсюда следует

или

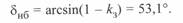
Значение  не зависит от длины линии и справедливо при 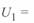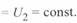. Иногда угол  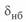называют углом по линии.

Используя полученные здесь выражения и значения , можно построить (см. рис. 3. 5) зависимость 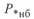 от длины линии, из которой следует, что натуральную мощность  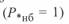можно передать лишь при длине линии 855 км, а при длине линии 1500 км 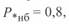, т. е. наибольшая мощность меньше натуральной. В практике возможны случаи, когда по соображениям динамической или результирующей устойчивости наибольшая передаваемая мощность ограничивается еще больше.

При уменьшении длины линии как максимальная, так и наибольшая передаваемая мощности возрастают и при очень малых длинах стремятся к бесконечности. Однако здесь вступает в силу ограничение, связанное с нагревом проводов линии и пропускной способностью коммутационной аппаратуры подстанций. Если говорить об ограничении по нагреву проводов, то оно зависит от марки проводов и температуры окружающего воздуха. Обычно оно лежит в пределах .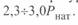

Для коротких линий, когда можно принять 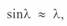, с учетом (3. 46) будем иметь хорошо известную формулу:

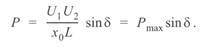                    (3. 49)

 

Ранее говорилось, что реактивная мощность линии СВН является одним из важных показателей ее режима.

Векторная диаграмма (см. рис. 3. 4) позволяет найти зависимость реактивной мощности 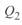 от угла 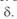. Из диаграммы следует, что

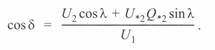
Определив отсюда значение 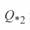 и учитывая, что

в результате получаем выражение для 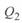 как функции угла :

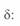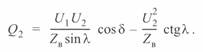                     (3. 50)

Построив векторную диаграмму по данным начала линии (3. 39). можно получить аналогичное выражение для 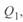, которое может быть использовано при расчете параметров режима по данным начала линии:

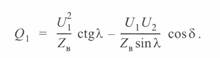                (3. 51)

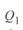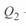Отметим, что  и  — реактивные мощности, которые генерируются или потребляются непосредственно самой линией.

На рис. 3. 6 приведены зависимост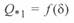и  и 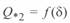 для линии длиной менее 1500 км. В них можно выделить две характерные точки. Одна из них — точка перехода этих величин через нуль, что соответствует передаче натуральной мощности; при этом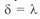

(см. ниже), что позволяет определить длину линии. Другая — это точка, где электрический угол 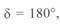, что соответствует противофазе напряжени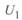й  и 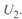. При этом ток достигает максимально возможного для этой линии значения. Однако в нормальных условиях такого режима быть не может. Он возможен лишь при асинхронном ходе связываемых систем.

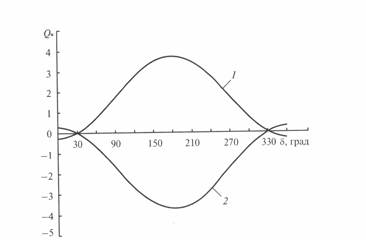
Рис. 3. 6. Зависимость реактивной мощности начала линии 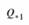 (кривая 1) и конца линии  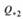(кривая 2) от угла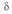

 

При нулевой длине линии, как это следует из (3. 50), значения 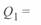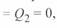, что соответствует физическим представлениям.

При  реактивные мощности равны:

 

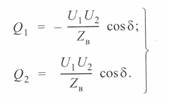                 (3. 52)

Вторая составляющая (3. 50) здесь отсутствует, так как .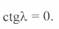

При длине линии свыше 1500 км котангенс в (3. 50) меняет знак и значения 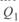 и 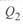  являются уже не разностью двух составляющих, а их суммой, поскольку при  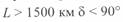(см. ниже). Это означает увеличение стоков реактивной мощности с линии по сравнению со случаем, когда .

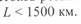Векторная диаграмма линии длиной менее 1500 км (см. рис. 3. 4) позволяет найти взаимосвязь между углом 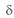 и волновой длиной линии. Взяв отношение двух катетов, будем иметь

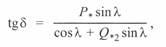                  (3. 53)

откуда следует, что угол сдвига между напряжениями по концам линии зависит не только от передаваемой активной мощности, но и от реактивной. В случае, если , то 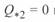 и при этом  , или .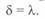

 

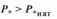Рис. 3. 7. Зависимость угла от длины линии при  (кривая 1), (кривая 2),  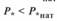(кривая 3)

 

Таким образом, при передаче натуральной мощности по идеализированной линии угол 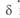всегда равен волновой длине линии. Это может служить контрольной точкой при проверке результатов расчета режима наибольших нагрузок, когда передаваемая мощность близка к натуральной. Учет активных сопротивлений проводов при расчете режима реальной линии относительно слабо скажется на значении 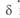, увеличив его на несколько градусов.

В режимах, значительно отличающихся от режима передачи натуральной мощности, например в режимах малых нагрузок, проявляется влияние реактивной мощности. Зависимость угла 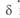 от длины линии при различных значениях 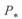, приведена на рис. 3. 7.

 

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: