 |
Тема 3.5. Уравнения длинной линии в относительных единицах
|
|
|
|
Выше были получены уравнения, в которых в параметры режима начала и конца линии, а также промежуточной точки входило комплексное значение тока. В то же время в практических расчетах режимов электрических систем и дальних линий электропередачи. как правило, используют значение мощности. Поэтому для удобства расчетов и придания им общности путем перехода к относительным единицам введем мощность в уравнения (3. 10)—(3. 13).
Предварительно условимся о положительных направлениях активной и реактивной мощностей. За положительное направление активной мощности принимается направление от начала к концу линии. За положительное направление реактивной мощности — направление, совпадающее с направлением активной мощности. Это значит, что на передающем конце положительное направление реактивной мощности — это направление от шин передающей подстанции к линии, на приемном — с линии на шины приемной подстанции. Как будет показано в дальнейшем, в некоторых режимах направления реактивных мощностей начала и конца линии могут быть противоположны направлению активной. В этом случае реактивная мощность меняет знак на отрицательный.
Далее приводятся выражения для расчета параметров режима реальной и идеализированной линий в относительных единицах.
Расчет по данным начала реальной линии. Полная мощность начала линии, при положительном значении ее реактивной составляющей может быть выражена как
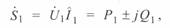
откуда прямой комплексный ток
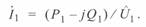(3. 32)
Подставив это значение тока в уравнение напряжения (3. 11), помножив и разделив второй член этого уравнения на прямое комплексное напряжение, получим промежуточное уравнение
|
|
|
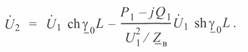
Введем базисную мощность начала линии. Для реальной линии это будет комплексная величина, поскольку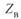 
имеет комплексный характер:
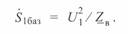(3. 33)
Разделив второй член промежуточного уравнения на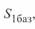 
, после преобразований будем иметь
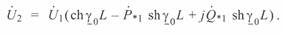(3. 34)
Подставив 
из (3. 32) в уравнение тока (3. 11), помножив и разделив первый член этого уравнения на произведение 
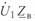, после преобразований получим
(3. 35)
В уравнениях (3. 34) и (3. 35) относительные величины составляющих мощности начала линии равны
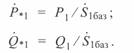
Следует отметить, что в этих уравнениях используются комплексные величины 
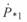, поэтому мощности 
и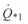 
будут также комплексными.
Мощность конца линии определяется как
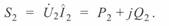(3. 36)
Положив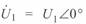 
, получим
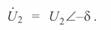
При заданных параметрах режима начала линии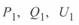 
и отсчете текущей координаты длины 
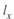также от начала линии параметры режима для некоторой промежуточной точки x определяются как
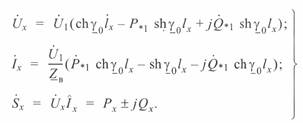(3. 37)
Расчет по данным начала идеализированной линии. Преобразования уравнений (3. 22) и (3. 23), аналогичные проведенным выше, приводят к следующим результатам.
Для некоторой промежуточной точки, находящейся на расстоянии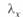 
от начала линии, можно записать:
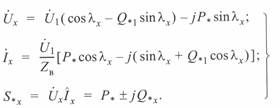(3. 38)
Здесь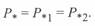 
.
Для конца линии имеем
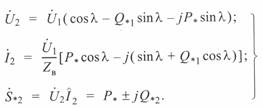(3. 39)
Отметим, что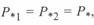 
, поскольку в соответствии с принятыми допущениями 
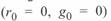потери активной мощности в линии отсутствуют. Для идеализированной линии базисная мощность есть действительная величина, поскольку 
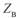также величина действительная
Расчет по данным конца реальной линии. Аналогичные уравнения могут быть получены и при заданных параметрах режима конца линии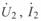 
.
Выразив ток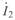 
через мощность и напряжение конца линии в (3. 12) подобно тому, как это было сделано при выводе уравнений для расчета по данным начала линии, и сделав соответствующие преобразования, для некоторой точки, расположенной на расстоянии 
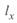от конца линии, получим:
|
|
|
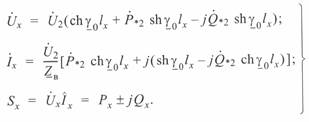(3. 40)
Для начала линии имеем:
(3. 41)
В уравнениях (3. 40) и (3. 41) относительные значения мощносте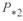й 
и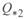 
определяются по базисным условиям конца линии:
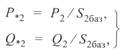(3. 42)
где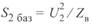 
.
Расчет по данным конца идеализированной линии. Для промежуточной точки, расположенной на расстоянии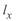 
от конца линии, уравнения (3. 40) записываются как
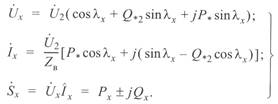(3. 43)
Для начала линии уравнения (3. 43) принимают вид:
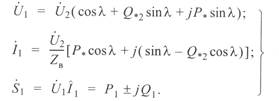(3. 44)
При расчетах параметров режима линии по данным конца удобно расположить вектор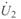 
по действительной оси
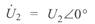
и угловые сдвиги всех величин определять от него, тогда
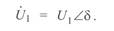
Уравнения (3. 37)—(3. 44) определяют связь между параметрами линии и параметрами режима. Из них следует, что при заданных параметрах линии и заданных напряжениях по ее концам по ней можно передать требуемую активную мощность лишь при строго определенных реактивных мощностях по концам линии.
|
|
|
