 |
Тема 5.1. Уравнения круговых диаграмм
|
|
|
|
Тема 5. 1. Уравнения круговых диаграмм
Поскольку круговые диаграммы линии отражают режимные параметры начала и конца линии, целесообразно воспользоваться математической моделью компенсированной линии, в которой линия представлена эквивалентным четырехполюсником. Коэффициенты этого четырехполюсника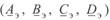 
учитывают все компенсирующие устройства, включенные в линию.
Напряжение и ток начала компенсированной линии связаны с такими же параметрами конца линии следующими уравнениями:
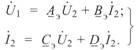(5. 1)
Найдем из первого уравнения (5. 1) ток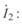 
Подставим его во второе уравнение (5. 1), и учтя, что
после несложных преобразований получим
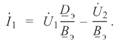
Полная мощность начала линии определяется выражением
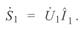
Подставив в это уравнение сопряженное комплексное значение тока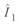 
, будем иметь
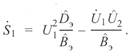
Примем, что вектор напряжения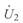 
совпадает с осью абсцисс 
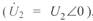, тогда 
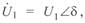, и окончательно получим
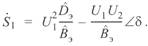(5. 2)
Это уравнение есть уравнение круговой диаграммы начала компенсированной линии. Оно же есть уравнение некомпенсированной линии, если коэффициенты четырехполюсника отражают только параметры самой линии.
В уравнении (5. 2), в котором используются коэффициенты эквивацентного четырехполюсника, учитывающие все элементы с сосредоточенными параметрами, включенные в линию, первый член уравнения есть координата центра окружности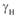 
(начало линии), второй — радиус-вектор 
, положение которого изменяется при изменении угла 
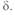. Положение центра окружности и значение радиуса-вектора являются функциями параметров и места расположения компенсируюiцих элементов, включенных в линию.
Найдем уравнение круговой диаграммы конца компенсированной линии.
Решив уравнения (5. 1) относительно напряжения и тока конца линии, получим
|
|
|
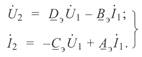(5. 3)
Найдя из первого уравнения (5. 3) ток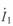 
, подставив его во второе уравнение и проделав преобразования, аналогичные предыдущему случаю, получим
Сориентировав, как и ранее, вектор напряжения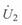 
по оси абсцисс 
, получим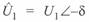 
. Окончательно будем иметь
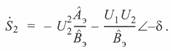(5. 4)
Это уравнение есть уравнение круговой диаграммы конца компенсированной линии. Здесь также первый член уравнения определяет положение центра окружности, второй член есть радиус-вектор.
Тема 5. 2. Круговые диаграммы компенсированных линий
Линия с шунтирующим реактором
В гл. 4. 4 были получены выражения для коэффициентов эквивалентного четырехполюсника (4. 44), замещающего линию с реактором. включенным в некоторой промежуточной точке:
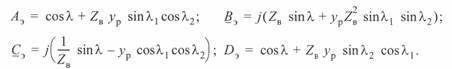
Из этих уравнений следует, что в общем случае коэффициенты 
и 
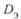при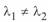 
не равны. Поэтому координаты центров круговых диаграмм начала и конца линии будут различны и сами круговые диаграммы будут несимметричны относительно оси абсцисс. Коэффициенты и 
могут быть равны только при включении реактора в середине линии, когда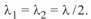 
. Тогда постоянные эквивалентного четырехнолюсника линии будут определяться следующим образом:
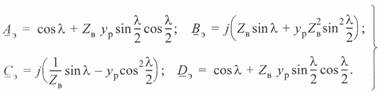(5. 5)
Для оценки влияния реактора, включенного в середине линии, сопоставим параметры круговых диаграмм некомпенсированной линии 500 кВ длиной 500 км и такой же линии с реактором. При этом проводимость реактора меняется в 2 раза — от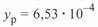 
до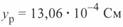 
(один или два таких реактора 500 кВ мощностью 180 Мвар каждый). Сама линия имеет следующие параметры: 
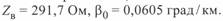. Сопоставляемые данные приведены в табл. 5. 1.
В этой таблице указаны координаты центра круговой диаграммы начала линии. Поскольку реактор включен в середине линии, то при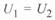 
координата центра круговой диаграммы конца имеет то же численное значение, но обратный знак. Реактивные мощности концов линии также равны по значению, но имеют разные знаки.
|
|
|
При включении реактора центр круговой диаграммы начала линии смещается вверх, а центр круговой диаграммы конца линии — вниз но отношению к центрам диаграмм некомпенсированной линии. Одновременно уменьшается значение радиуса-вектора. Смещение центра круговых диаграмм и уменьшение радиуса-вектора тем больше, чем больше проводимость (мошность) реактора (рис. 5. 1). Все это приводит к тому, что в режиме малых нагрузок, в частности в режиме холостого хода при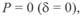 
, реактивная мощность, стекающая с концов компенсированной линии и равная
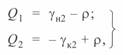(5. 6)
уменьшается по сравнению с реактивной мощностью некомпенсированной линии. Это соответствует физическим процессам, происходящим в компенсированной линии, поскольку часть зарядной мощности последней поглощается реактором.
Таблица 5. 1
Параметры круговых диаграмм некомпенсированной линии и линии с реакторами разной проводимости
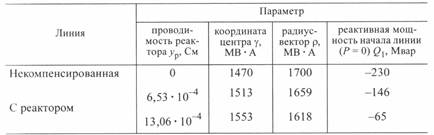
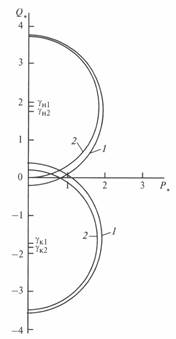
Рис. 5. 1. Круговые диаграммы идеализированной некомпенсированной линии (U = 500 кВ, L = 500 км) (кривая 1) и линии с шунтируюшим реактором (кривая 2) в ее середине (проводимость реактора yp = 13, 06х10-4 См)
Следует также отметить, что уменьшение радиуса-вектора свидетельствует снижении пропускной способности компенсированной линии. Это снижение достаточно заметно (около 9, 5 % при одном реакторе и 19 % при двух реакторах). Однако главная задача при включении реактора в середине линии заключается в снижении напряжения в этой точке в режиме малых нагрузок. Поэтому некоторое уменьшение пропускной способности в этом режиме неопасно, поскольку в режиме больших нагрузок реактор должен быть отключен.
Рассмотрим, каким образом перемещение точки включения реактора влияет на параметры круговых диаграмм линии. Возьмем предельные случаи.
Реактор включен в начале линии: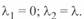 
. В этом случае параметры эквивалентного четырехполюсника линии будут записаны как
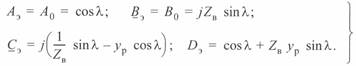(5. 7)
Реактор включен в конце линии: 
. Постоянные четырехполюсника здесь определяются следующим образом:
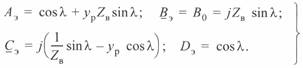(5. 8)
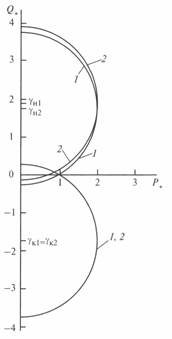
Рис. 5. 2. Круговые диаграммы некомпенсированной линии (1) и линии с реактором, включенным в ее начале (2)
Уравнения (5. 7) и (5. 8) позволяют сделать следующие выводы:
при включении реактора в начале или конце линии значение радиуса-вектора будет таким же, как у некомпенсированной линии. Это объясняется тем, что напряжения по концам линии приняты неизменными. Поэтому включение реактора не оказывает влияния на пропускную способность линии;
|
|
|
при включении реактора в начале линии центр диаграммы начала линии будет смещен вверх по отношению к центру диаграммы некомпенсированной линии, а центр диаграммы конца линии и сама диаграмма совпадают с круговой диаграммой некомпенсированной линии. При включении реактора в конце линии взаимное расположение круговых диаграмм будет обратное.
Круговые диаграммы при включении реактора в начале и конце линии приведены на рис. 5. 2.
|
|
|
