 |
Тема 4.2. Методы учета распределённости параметров в схемах замещения линии
|
|
|
|
Тема 4. 2. Методы учета распределённости параметров в схемах замещения линии
Метод прямого вычисления параметров схем замещения
Рассматриваемый метод предполагает использование уравнений (4. 7) или (4. 9) без каких-либо упрощений и допущений, поэтому он наиболее точен.
Зная удельные погонные параметры линии, можно определить комплексные значения волнового сопротивления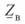 
и коэффициента распространения электромагнитной волны 
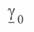и, подставив их в указанные уравнения, получить конечный результат.
Расчет производится на компьютерах, имеющих соответствующее программное обеспечение типа Mathcad, Mathlab и др.
Метод поправочных коэффициентов
Выразив сопротивление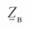 
в выражении для 
(4. 7) через удельные параметры линии, помножив и разделив подкоренное выражение на 
, будем иметь:
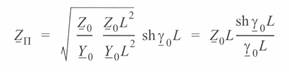
или
(4. 11)
где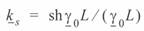 
- поправочный коэффициент, учитывающий распределенность параметров линии.
При малых значениях аргумента (малой длине линии)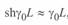 
, 
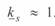
Поэтому в этих случаях сопротивление продольной ветви схемы замещения 
можно определять просто как произведение удельного погонного параметра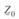 
на длину линии 
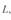., что обычно и делается. Однако при значительной длине линии значение 
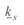будет заметно отличаться от единицы, причем это различие будем тем больше, чем больше длина линии. Поэтому для достаточно протяженных линий учет этого коэффициента обязателен.
Аналогичные преобразования могут быть проделаны и для выражения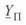 
(4. 3). Помножив и разделив правую часть этого уравнения на 
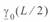и учтя выражения для 
и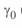 
(3. 17) и (3. 20), после преобразований получим:
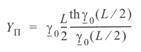
или
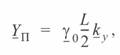(4. 12)
|
|
|
где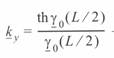 
- поправочный коэффициент, для которого справедливы все соображения, приведенные выше для коэффициента 
.
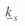В практических расчетах использование коэффициентов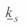 
и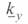 
в том виде, в каком они приведены выше, достаточно сложно. Поэтому упростим их, воспользовавшись разложением в ряд.
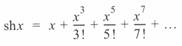
Отметим, что этот ряд не знакопеременный в отличие от ряда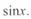 
. Учитывая, что здесь 
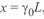получаем
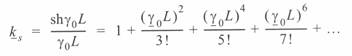
или
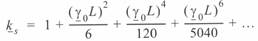(4. 13)
Разложение в ряд гиперболического тангенса имеет вид
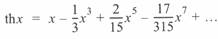
Учитывая, что в данном случае
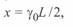
и подставляя это значение в выражение для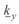 
, будем иметь
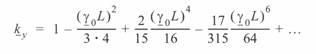
или
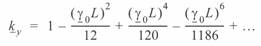(4. 14)
Отделив действительные и мнимые части в выражениях (4. 13) и (4. 14) и отбросив члены ряда далее второго в силу их малости, получим поправочные коэффициенты для определения активных и реактивных сопротивлений и проводимостей П-образной схемы замещения:
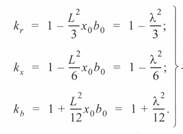(4. 8)
Выражение поправочного коэффициента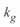 
, для определения значения активной проводимости 
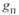не приводится, так как потери мощности и энергии на корону учитываются не введением этой проводимости в схему замещения линии, а другими методами.
При использовании этих коэффициентов параметры П-схемы замещения определяются как
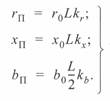
В практических расчетах для линий длиной до 250 км поправочные коэффициенты близки к единице и поэтому обычно не учитываются. Погрешность при этом составляет 1—2 %, что вполне допустимо для инженерных расчетов. Для линий большей длины учет поправочных коэффициентов обязателен. Следует подчеркнуть, что он также обязателен и при вводе исходных данных по ветвям (для линий длиной более 250 км) в расчетные программы на ЭВМ.
|
|
|
Для линий длиной свыше 600 км следует использовать другие методы, поскольку упрощения, принятые при выводе выражений (4. 15) (разложение в ряд и отбрасывание членов после второго) приводят к заметным погрешностям. Таким образом, диапазон длины линий, в котором следует применять поправочные коэффициенты, составляет 250—600 км.
|
|
|
