 |
9.1. Случай, когда все стратегии активные
|
|
|
|
УДК 510. 22
Теория игр: Учеб. пособие/Н. В. Мурзов, А. В. Дубовиков, Рязан. Гос. радиотехн. акад. Рязань, 2001. 68 с. ISBN5-7722-0178-6.
Содержит изложение курса лекций, прочитанных авторами студентам
РГРTА.
Предназначено для студентов всех специальностей.
Игра, стратегия, функции выигрыша, матрицы игры, коалиция, характеристическая функция, вектор Шепли
Печатается по решению редакционно-издательского совета Рязанской государственной радиотехнической академии.
Рецензент: кафедра высшей математики Рязанской государственной радиотехнической академии (зам. кафедрой А. И. Новиков)
| Мурзов Николай Васильевич |
Дубовиков Андрей Викторович
ТБОРИЯ ИГР
Учебное пособие
Редактор И. П. Перехрест
Корректор: М. Е. Цветкова
Подписано в печать 05. 12. 2001. Формат бумаги 60х84 1/16.
Бумага газетная. Печать офсетная. Усл. печ. л. 4, 25.
Уч. -изд. л. 4, 25. Тираж 50 экз. Заказ 718 ц10-50
Рязанская государственная радиотехническая академия.
391000, Рязань, ул. Гагарина, 59/1.
Редакционно-издательский центр РГРТА.
ISBN 5-7722-0178-6 ©Рязанская государственная радиотехническая академия, 2001
Светлой памяти
Николая Васильевича Мурзова
посвящается это издание
Предисловие
Предлагаемое учебное пособие написано на основе лекций, читаемых авторами студентам РГРТУ специальности " Математические методы и исследования операций в экономике". Введение и глава " Матричные игры" написаны Н. В. Мурзовым, глава " Кооперативные игры" и " Приложение" -А. В. Дубовиковым. Минимальные сведения о теории вероятностей, необходимые для понимания материала, содержатся в приложения. Знак ⊗ обозначает конец доказательства.
|
|
|
Введение
Теория игр, обязанная своим происхождением так называемым салонным играм, и мест многочисленные экономические, социологические и военные приложения. Эти приложения поддерживают интерес к теории игр и питают ее новыми задачами. Тем не менее в ней сохранилась в значительной степени первоначальных терминология, относящаяся к играм в собственном смысле: партия, ход, выигрыш, игрок и др. Первые серьезные исследования по теория ягр были выполнены в первой трети ХХ века такими выдающимися учеными, как Э. Иермело, Э. Борель, Дж. фон Нейман, но не породила сколь-нибудь заметных откликов, И только после публикации книга Дж. фон Неймана н-О. Моргенштерна " Теория игр и экономическое поведение" (первое издание книги появилось в 1943 году, русский перевод Был выполнен с третьего американского издания 1953 года и вышел из печати в 1970 году) началось интенсивное развитие теории игр и ее приложений.
Теория игр является частью большого и интенсивно развивающегося раздела математики " Исследование операций" - теории математических моделей принятия оптимальных (в определенном смысле) решений, Принятие решений осуществляется при различном уровне информированности принимающего решение субъекта о создавшейся ситуации, В полностью детерминированном случае при возможности количественной оценки результата принятия того или иного решения (т. е. при заданной целевой функция) задача сводится, как правило, к поиску экстремума функции нескольких переменных при заданных ограничениях. Типичным примером такого рода является классическая " транспортная задача" [1. 4]
В другом случае информированности субъекту необходимо принимать решение, когда имеется несколько вариантов условий, он не знает, какой из них может осуществиться в действительности, но ему известно априорное распределение вероятности появления каждого из вариантов. В этом случае дело сводится к поиску экстремума среднего значения (математического ожидания) целевой функции. При всей содержательной несхожести указанных случаев в принципе они сводятся к математически однотипным задачам.
|
|
|
В третьем случае информированности субъекту может быть известным только множество вариантов; а распределение вероятности на этом множестве неизвестно. Более того, выбор варианта может находиться во власти другого (других) разумного субъекта (игрока), интересы которого не обязаны совпадать с интересами первого субъекта. Именно этим третьим случаем занимается теория игр. Поэтому ее можно определить [5] как теорию математических моделей принятия оптимальных решений в условиях конфликта или неопределенности.
Понятие " конфликт" подразумевает задание множества то участников, их возможностей и интересов [5, 6]. " Оптимальность" предусматривает задание системы предпочтений, позволяющих сравнивать между собой решения. Включение в определение теории игр " неопределенности" отражает возможность применения ее (теории игр) методов к принятию решений в ситуации, когда разумный противоборствующий субъект отсутствует, но, когда ничего не известно о шансах появления того или иного варианта условий, в которых необходимо принимать решение, и приходится, например ввиду большого риска или осторожности, рассчитывать на осуществления наихудшего варианта. Такого рода задачи объединяются термином " игры против природы". С чисто качественной стороны все игры можно условно разбить на три группы: азартные, комбинаторные, стратегические [7]. (Хотя, конечно, многие реальные игры содержат в себе все три аспекта. )
С чисто качественной стороны все игры можно условно разбить на три группы: азартные, комбинаторные, стратегические [7]. (Хотя, конечно, многие реальные игры содержат в себе все три аспекта. )
Типичными азартными играми являются: " орлянка", рулетка, всевозможные варианты игры в " кости". Основным элементом этих игр является, то, что исход игры определяется исключительно случайным фактором и не зависит от умения игрока. Анализ азартных игр относится к теории вероятностей и не является объектом изучения собственно теории игр.
|
|
|
Основным объектом изучения теории игр являются стратегические игры. Простейшим примером стратегической игры, в которой, тем не менее, проглядывается вся суть игр этого класса, является игра типа чет-нечет. В игре участвуют два игрока. Первый игрок зажимает в кулаке несколько предметов, а второй пытается угадать: четное или нечетное число предметов находится у первого игрока. Если он угадал, то он выиграл, в противном случае выигрывает первый игрок. В другой разновидности этой игры игроки независимо друг от друга одновременно кладут на стол по монете. Если оказалось, что монеты выложены оной стороной, то выигрывает один игрок, в противном случае выигрывает другой игрок.
Стратегическими являются большинство карточных игр, всевозможные игры на " пальцах" (например, " two fingersMorra" [16]). Многие экономические, социальные, военные проблемы имеют характер именно стратегических игр (см. например, [17], [20] др. ).
Обычно в реальных условиях игры протекают в развернутой форме, когда игроки делают ходы поочередно. При этом различают личные ходы, когда игрок делает тот или иной выбор, н случайные ходы, когда выбор осуществляется некоторым случайным (рандомизирующим) механизмом (например, сдача карт). Игру развёрнутой форме можно представить в виде дерева (графа) игры, представляющего собой плоскую фигуру, состоящую из точек (вершин графа), обозначающих позиции в игре, и прямолинейных отрезков, обозначающих ходы, возможные в данной позиции. (Пример дерева игры будет дан ниже. ) В соответствии с правилами игры игрок может оказаться не в состоянии отличить друг от друга некоторые из вершин графа при своем ходе (например, после случайного хода). Множество таких вершин называется информационным множеством. Обычно на дереве игры вершины, принадлежащие одному информационному множеству, обводятся пунктирной линией. Если все информационные множества содержат только одну вершину, то игра называется игрой с полной информацией. После того как произведено разбиение всех вершин на информационные множества, стратегию игрока можно определить как функцию, определённую на классе его информационных множеств. Иными словами, стратегия — это набор правил, позволяющих осуществить вполне определенный выбор игроком при каждом своем холе. Выбор игроками определенных стратегий задает некоторую партию в игре, в которой каждый игрок получает полагающийся ему по правилам выигрыш. Итак, игру можно представить происходящей таким образом: каждый игрок предъявляет свою стратегию и получает соответствующий выигрыш. Представленная в таком виде игра называется игрой в нормальной форме. Ввиду важности этого понятия дадим его формальное определение
|
|
|
 Бескоалиционной игрой в нормальной форме называется система
Бескоалиционной игрой в нормальной форме называется система
(1)
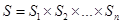 и который I={1, 2, …, n}-множество игроков, Si, i
и который I={1, 2, …, n}-множество игроков, Si, i 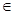 I, - множество стратегической i-го игрока, Hi, i
I, - множество стратегической i-го игрока, Hi, i 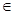 J, - функция выигрыша i-го игрока, определенная на декартовом произведении
J, - функция выигрыша i-го игрока, определенная на декартовом произведении
(2)
 Элемент s=(s1, s2, …, sn), si
Элемент s=(s1, s2, …, sn), si 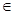 Si, i
Si, i 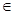 I, декартова производная (2) называется ситуацией. Таким образом, выигрыш каждого игрока является функцией, определенной на множестве всех ситуаций:
I, декартова производная (2) называется ситуацией. Таким образом, выигрыш каждого игрока является функцией, определенной на множестве всех ситуаций:
Термин " бескоалиционная" подчеркивает, что усилия каждого игрока направлены на получение по возможности большего индивидуального выигрыша, а не на максимизацию выигрышей коалиций (коллективов) с последующим разделением между игроками.
Представление игр в нормальной форме удобно точки зрения их общего теоретического анализа. Однако при рассмотрении конкретной игры удобнее ее представление в развернутой форме.
В зависимости от структуры входящих в (1) элементов можно осуществить примерную классификацию игр. По числу участников: различают игры 2 лиц и игры n(n> 2) лиц. По числу стратегий у каждого игрока: если каждое из множеств Si, i 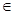 I, - конечное, то игра называется конечной, в противном случае - бесконечной. По интересам игроков: если
I, - конечное, то игра называется конечной, в противном случае - бесконечной. По интересам игроков: если
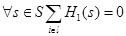 (3)
(3)
то игра называется игрой с нулевой суммой, в противном случае - играй с ненулевой суммой.
Игра 2 лиц с нулевой суммой называется антагонистической, в ней

Поэтому обычно выигрыш первого игрока обозначают просто H(s) тогда выигрыш второго есть -H(s). (Иначе говоря, H(s) есть проигрыш
второго игрока. )
Если в антагонистической игре 2 ниц множества S1, S2, конечны, то- игра называется матричной. Название объясняется тем, что игру можно представить таким образом: элементы множеств S1, S2. занумеровываются, например
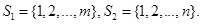
Ситуацией в этом случае является пара (i, j); i= 1, 2, m; j= 1, 2, …, n. Выигрыш первого игрока H(i, j) рассматривается как элемент а, матрицы А размером п п. А называется матрицей игры. Игра протекает следующим образом: игроки одновременно н независимо друг от друга называют номер строки (первый игрок) и номер столбца (второй игрок): Элементу матрицы, расположенный на пересечении выбранных строки и столбца, есть выигрыш первого игрока и соответственно проигрыш второго.
|
|
|
Приведенная классификация далеко не исчерпывает всего многообразия игр. Более подробно об этом см. [5].
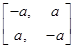 Дадим несколько примеров игр.
Дадим несколько примеров игр.
Пример 1. Чет-нечет. Это пример простейшей матричной игры с матрицей
Стратегии первого игрока:
i=1- взять четное число предметов,
i=2- взять нечетное число предметов;
стратегии второго игрока:
j=1- назвать " чет",
j=2- назвать " нечет",
а - положительное число, ставка в агрессора.
Пример 2. Проблема полковника Блотто [11], [20]
Две воюющие армии ведут борьбу за два пункта. Первая армия под
командованием полковника Блотто состоит из 4 полков, вторая под командованием капитана Киже - из 3 полков. Армия, которая посылает больше полков на тот кли иной пункт; занимает его н уничтожает все натравленные на этот пункт силы противоположной стороны, получая 1 балл как за занятый пункт, так за каждый уничтоженный полк противника. Требуется распределить силы так, чтобы получить максимальное количество баллов.
Это матричная игра с матрицей
Киже
 |
Слева и сверху указаны стратегии игроков. Стратегия (а, b) обозначает, что игрок посылает (а) полков на первый пункт и (b) полков на второй.
Пример 3. " Веришь - не веришь" [1]
Имеется две карты: туз (T) и двойка(Д). Первый игрок случайным образом берет одну из них. Если у него оказался Т., то он, не показывая карты, объявляет " у меня туз". Второй игрок может сказать " верю" и, не глядя на карту, отдать первому і у. е. (единицу ставки в игре). Но он может сказать " не верю" и потребовать показать карту. Поскольку первый игрок действительно имеет туза, то в этом случае второй игрок уплачивает первому 2 yе.
Если у первого игрока оказалась двойка, то он имеет две возможности: не показывая карты, объявить " у меня туз" или " у меня двойка". Если он сказал " у меня туз", то второй игрок может сказать " верю" и, не глядя на карту, отдать первому 1 у. е но может сказать " не верке' и потребовать показать карту. Поскольку у первого игрока действительности не туз, то второй игрок получает от первого 2 у. е. И, наконец, если первый игрок, имея двойку, говорит " у меня двойка", то он уплачивает первому 1 у. е., которую тот и берет. Изобразим дерево этой игры (см. рис. 1).
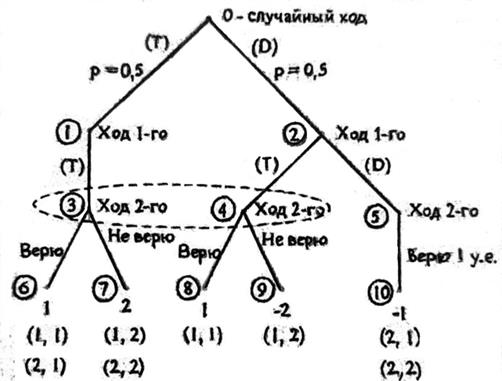
Рис. 1
Цифры 1, 2, …, 10 обозначают номер позиции. Позиции 3, 4 составляют информационное множество 2-го игрока. Цифры в скобках обозначают стратегии игроков:
для первого игрока:
i = 1- в позиции он говорит " у меня туз";
в позиции 2 он тоже говорит " у меня туз";
i = 2 - в позиции 1 он говорит " у меня туз";
в позиции 2 он говорит " у меня двойка";
для второго игрока:
j= 1 - в информационном множестве {3, 4} он говорит " верю";
в позиции 5 берет балл;
j= 2- в информационном множестве {3, 4} он говорит " не верю";
в позиция 5 берет 1 балл.
Позиции 6-10 являются окончательными. Около них записаны выигкрыши первого игрока (пронтрыши второго) и ситуация, приводящие игру в каждую из этих позиций.
Подсчитаем выигрыши в каждой из ситуаций.
 В ситуации (1, 1) игра может закончиться с вероятностью 0. 5 в позиции6 и с вероятностью 0. 5 в познин 8. В каждой яз них выигрыш первого игрока равен единице Поэтому среднее вынгрын (математическое ожидание) вычисляется по
В ситуации (1, 1) игра может закончиться с вероятностью 0. 5 в позиции6 и с вероятностью 0. 5 в познин 8. В каждой яз них выигрыш первого игрока равен единице Поэтому среднее вынгрын (математическое ожидание) вычисляется по
формуле:
В ситуации (1, 2) игра может закончиться с вероятностью 0. 5 в позиции 7 и
стакой же неронтностыо в позиции 9. Для среднего выигрыша имеем:
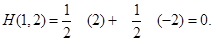 |
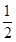
В ситуации (2. 1) игра может закончиться с вероятностью в позиции 6 и
такой же вероятностью в позиция 10. Для среднего выигрыша имеем:
 |
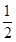
 |
В снтуацяи (2, 2) ра ножет закончиться с вероятностью в позяции 7 и стакой же вероягностью в позиция 10. Позтому
Таким образом, получаем матричную игру с матрицей
j=1 j=2
 |
Пример 4. " Поиск на отрезке" [20]
Игрок 1 (ищущий) выбирает точку х 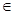 [0; 1]. Игрок 2 (прячущийся) выбирает одновременно и независимую точку у
[0; 1]. Игрок 2 (прячущийся) выбирает одновременно и независимую точку у 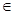 [0, 1]. Задано некоторое положительное число τ. Если х-у≤ τ, то игрок 2 считается обнаруженным этом случае полагает
[0, 1]. Задано некоторое положительное число τ. Если х-у≤ τ, то игрок 2 считается обнаруженным этом случае полагает
 |
Если |x-y|> τ, то
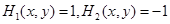 |
Это пример бесконечной антагонистической игры, так называемой" игры на сливочном квадрите".
Если интепретировать x, y как моменты времени, которые игроки прибывают в заданное место, а так время, и течение которого они там находятся, то данная задача может рассматриваться, как " задача о встрече",
в которой игрок 1 стремится к встрече, а игрок 2 стремится избежать ее
Пример 5. " Семейный спор" [15]
Муж, игрок 1, и жена, игрок 2, могут выбирать одно из двух вечерних развлечений: посещение матча по бутову (стратегии 1=1, j=1) или послещение балета (стратегии i=2, j=2) Согласно обычному стандарту, мунчща предпочитает футбол, а женщина - балет, однако обоим торнадо важнее инти вместе, чем поодиночке смотреть предпочитаемое зрелище, Выдрыши игроков можно записать (в условных единицах полезности) в виде следующих матриц:
j=1 j=2 j=1 j=2
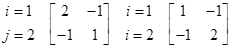 |
H1(. ) H2(. )
это пример антагонистической (биматричной) игры. Бе анализ дается в §2 главы " Кооперативные игры".
Пример 6. " Дилемма фермера" [15]
Дна фармера, обеспечивающие рынок пшеницы в заданном регионе, имеют возможность засеять одно на два разных по площади поля пшеницей. Урожайность на всех волях одинакова Затраты на получение урожая с одного поля равны а (у. е. ). Если оба фермера засеют по одному полю (стратегии і=1, j1), то стоимость урожая, собранного с одного поля, равная S(у. е. ). Если один из фермеров засеять одно поле, упругой - да, то стоимость урожая, собранного с одного поля, понизится, но незначительно составит S- с (у. е). Если оба фермера засеют по два поля (стратегии i=2, j=2), то стоимость урожая,
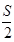 |
собранного с одного поля, понизится в два раза. и составит (y. е. ).
Вычислим выигрыная каждого из фермеров
H1(1, 1)=S·1 - a; H2(1, 1)=S·1 - a;
H1(1, 2)=(S - ε )·1 - a; H2(1, 2)=(S - ε )·2 - 2a;
H1(2, 1)=(S - ε )·2 - 2a; H2(2, 1)=(S - ε )·1 - a;
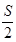

H1(2, 2)= ·2 - 2a; H2(2, 2)= ·2 - 2a;
Полагая, для примера, S= 20, a= 5, с = 4, получаем матричную игру с матрицами:
j=1 j=2 j=1 j=2
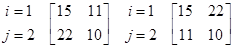
H1(. ) H2(. )
Любопытно отметить своеобразное обстоятельство, присуще играм такого типа. Фермерам, с одной стороны, выгодно действовать согласованно и, выбрав стратегий (1, 1), получать по 15 у. е. Но, договорившись об этом, каждому из них выгодно (если не учитывать угрызений совести или страха от нарушения договора) отклонить от договора и получить 22 у. е. вместо 15. Однако если так поступят оба игрока, то они окажутся оба в проигрыше, получив 10 у. е. вместо 15. Эта игра анализируется в §2 главы " Кооператив-
вые игры".
Пример 7. " Охрана окружающей среды" [20]
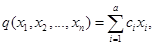 В промышленном районе расположено п предприятий, каждое из которых выбрасывает в атмосферу вредную смесь: Объем выброса і-го предприятия i=1, в обозначены через хi, 0 ≤ хi ≤ a, где а - заданная величина. В районе имеется экологически значимая зона, уровень загрязнений в которой не должен превышать предельно допустимого значения. Предположим, что средний уровень концентрации вредной смеси в данной зоне может быть вычислен по формуле
В промышленном районе расположено п предприятий, каждое из которых выбрасывает в атмосферу вредную смесь: Объем выброса і-го предприятия i=1, в обозначены через хi, 0 ≤ хi ≤ a, где а - заданная величина. В районе имеется экологически значимая зона, уровень загрязнений в которой не должен превышать предельно допустимого значения. Предположим, что средний уровень концентрации вредной смеси в данной зоне может быть вычислен по формуле
(4)
| l, n |
где сi, i =, - заданные коэффициенты.
Пусть Ɵ - значение предельно допустимой концентрации (ДК) вредной смеси. Предположим, что каждое предприятие может снижать свои эксплуатационные расходы, увеличивая объем выброса, но если уровень загрязнения в зоне превышает ПДК, то на предприятие накладывается штраф Si > 0.
Пусть игрок і (предприятие) имеет возможность выбирать значения хi
из знакомства [0; а]. Функция выигрыша і-го игрока и мест вид
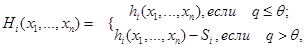 |
где h (х, …, х) - непрерывная и возрастающая по аргументу х, функция. Это пример игры n лиц ненулевой суммой.
МАТРИЧНЫЕ ИГРЫ
1. Экстреумы
В этом параграфе даны некоторые сведения об экстремумах функций одной и нескольких переменных, которые будут использоваться в дальнейшем изложении.
Пусть R - множество вещественных чисел. Множество 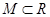 называется ограниченным сверку, еcли (и только если)
называется ограниченным сверку, еcли (и только если)
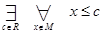
Любое число c, удовлетворяющее (1), называется верхней гранью (границы) множества M.
Наименьшая верхняя грань называется точной верхней гранью и обозначается sup M(supremum). Всякое ограниченное сверху множество имеет точную верхнюю грань, которая может как принадлежать, так и не принадлежать ему. Например, sup 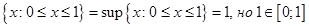
 . По определению для множества, не ограниченного сверху полагают sup M
. По определению для множества, не ограниченного сверху полагают sup M  . Заменив в (1) знак
. Заменив в (1) знак 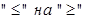 , получим определения множества, ограниченного снизу. Наибольшая нижняя грань называется точной нижней гранью и обознается inf M (infimum). Всякое ограниченное снизу множество имеет точную нижнюю грань. Для множества, не ограниченного снизу, по определению полагают inf M
, получим определения множества, ограниченного снизу. Наибольшая нижняя грань называется точной нижней гранью и обознается inf M (infimum). Всякое ограниченное снизу множество имеет точную нижнюю грань. Для множества, не ограниченного снизу, по определению полагают inf M 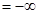 . Очевидно, что
. Очевидно, что
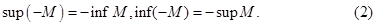
где обозначено  , а также
, а также
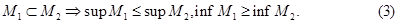
Рассмотрим функцию f(x), определенную на множестве 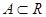 , и
, и
пусть f(A) – множество ее значений
Супремумом функции f(x) на А называется sup f(A) и обозначается 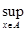 f(x).
f(x).
Если супремум функции достигается на A, т. е если существует такое 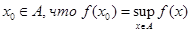 , то он называется максимумом (наибольшим значением) и обозначается
, то он называется максимумом (наибольшим значением) и обозначается 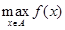 . Аналогично, если достигается инфимум, то он называется минимимом (наименьшим значением) и обозначается
. Аналогично, если достигается инфимум, то он называется минимимом (наименьшим значением) и обозначается  . Супремум и инфимум имеют любые функции, чего нельзя сказать о максимуме и минимуме. Например, функция
. Супремум и инфимум имеют любые функции, чего нельзя сказать о максимуме и минимуме. Например, функция  - дробная часть числа x – не имеет наибольшего значения. Существования максимума и минимума гарантируется теоремой Вейерштрасса, согласно которой функции непрерывные на замкнутом ограниченном множестве, имеют максимум и минимум. В этом пособии предполагается, что все рассматриваемые функции имеют максимум и минимум.
- дробная часть числа x – не имеет наибольшего значения. Существования максимума и минимума гарантируется теоремой Вейерштрасса, согласно которой функции непрерывные на замкнутом ограниченном множестве, имеют максимум и минимум. В этом пособии предполагается, что все рассматриваемые функции имеют максимум и минимум.
Из определения непосредственно следует, что
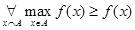 , (4)
, (4)
 , (5)
, (5)
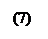
 , (6)
, (6)
, 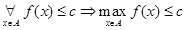

 ,
,
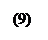
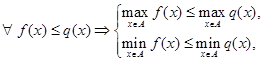

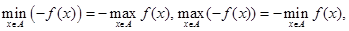
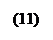
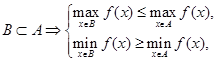
Таким образом, операции 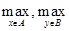 , а также
, а также  коммутативны. Иначе дело обстоит с коммутативностью операций
коммутативны. Иначе дело обстоит с коммутативностью операций 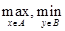 . В общем случае они не коммутативны.
. В общем случае они не коммутативны.
Лемма 1 (неравенство для минимаксов)
Для любой функции f(x, y), определённой на A x B: 0


Определение. Точка 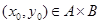 называется седловой точкой функции f (x, y), если
называется седловой точкой функции f (x, y), если


Заметим, что переменные x, y в определении седловой точки входят не симметрично и точка 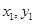 , для которой
, для которой
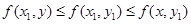 ,
,
седловой не является. Этим понятие седловой точки игр отличается от аналогичного понятия в геометрии, где седлообразность точки не зависит от направлений, в которых функция двух переменных возрастает или убывает. В теории игр, напротив, чтобы точка была седловой, необходимо, чтобы в ней достигался максимум именно по первой координате и минимум – во второй. Функция может иметь много седловых точек.
Так, например, для функции  каждая из точек вида
каждая из точек вида 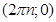
 является седловой.
является седловой.
Теорема 1. Если 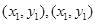 – две седловые точки функции f(x, y), то точки
– две седловые точки функции f(x, y), то точки  тоже будут седловыми и
тоже будут седловыми и
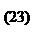

Теорема 2 (о седловой точке) Пусть f(x, y) – вещественная функция определённая на
 , и существует
, и существует
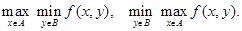
Для того чтобы
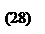
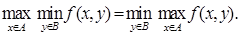
необходимо и достаточно, чтобы f(x, y) имела хотя бы одну седловую точку.
Следствие 1. Если 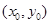 – седловая точка функции f(x, y) на
– седловая точка функции f(x, y) на  ,
,
то
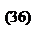
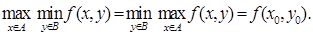
Следствие 2. Если точка 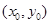 является седловой точкой функции f(x, y) на
является седловой точкой функции f(x, y) на  ,
,
то 
Итак, при равенстве максимина и минимакса (и только в этом случае) функция имеет хотя бы одну седловую точку и все множества седловых точек есть 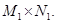 Если же максимин не равен минимаксу, то несмотря на то, что множество
Если же максимин не равен минимаксу, то несмотря на то, что множество 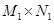 не пусто, ни одна из его точек не является седловой, поскольку их вообще нет.
не пусто, ни одна из его точек не является седловой, поскольку их вообще нет.
2. Принцип минимакса
Рассмотрим матричную антагонистическую игру  с матрицей
с матрицей 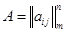 . Первый (максимизирующий) игрок выбирает строку, второй (минимизирующий) игрок выбирает столбец, на пересечении выбранных строки и столбца записан выигрыш 1-го игрока (проигрыш 2-го игрока). Каждый игрок стремится к увеличению своего выигрыша. Но его выигрыш зависит не только от его выбора, но и от того, какая стратегия будет выбрана противником. Поэтому, стремясь получить максимальный выигрыш, каждый игрок должен учитывать поведение противника. В теории игр выбор оптимальной стратегии предлагается осуществлять, основываясь на принципе минимакса (максимина), который иногда еще называют «принципом осторожной игры против умного партнера».
. Первый (максимизирующий) игрок выбирает строку, второй (минимизирующий) игрок выбирает столбец, на пересечении выбранных строки и столбца записан выигрыш 1-го игрока (проигрыш 2-го игрока). Каждый игрок стремится к увеличению своего выигрыша. Но его выигрыш зависит не только от его выбора, но и от того, какая стратегия будет выбрана противником. Поэтому, стремясь получить максимальный выигрыш, каждый игрок должен учитывать поведение противника. В теории игр выбор оптимальной стратегии предлагается осуществлять, основываясь на принципе минимакса (максимина), который иногда еще называют «принципом осторожной игры против умного партнера».
Вот рассуждения 1-го игрока, основанные на указанном принципе. «Пусть я выбрал і-ю строку. Тогда самое менышее, на что я могу рассчитывать будет 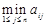 . Поэтому естественно выбрать такую строку
. Поэтому естественно выбрать такую строку  , чтобы этот минимальный выигрыш был наибольшим, т. е. чтобы
, чтобы этот минимальный выигрыш был наибольшим, т. е. чтобы
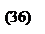
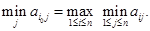
Таким образом, я могу гарантировать, что меньше, чем (38), мой выигрыш быть не может».
Величина (38) называется нижним значением игры и обозначается
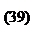
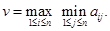
Значение  называется максиминной стратегией 1-го игрока. В терминах предыдущего параграфа
называется максиминной стратегией 1-го игрока. В терминах предыдущего параграфа 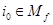 , если положить по определению
, если положить по определению
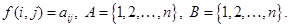
Рассуждения 2-го игрока, основанные на принципе минимакса. «Пусть я выбрал j-й столбец. Тогда самое большее, что я могу проиграть, – это

Поэтому естественно выбрать такой столбец 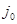 , чтобы этот максимальный проигрыш был наименьшим, т. е. чтобы
, чтобы этот максимальный проигрыш был наименьшим, т. е. чтобы
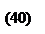

Таким образом, я могу гарантировать, что больше, чем (40), мой проигрыш быть не может.
Величина (40) называется верхним значением игры и обозначается

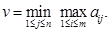
Значение 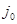 называется минимаксной стратегией 2-го игрока. В терминах первого параграфа
называется минимаксной стратегией 2-го игрока. В терминах первого параграфа 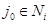 , где f(i, j) =
, где f(i, j) = 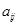 . Из (20) следует, что для любой матрицы А нижнее значение игры не превосходит верхнего
. Из (20) следует, что для любой матрицы А нижнее значение игры не превосходит верхнего

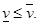
Впрочем, этот результат очевиден из предыдущих рассуждений.
Максимин и минимакс могут быть найдены по следующей схеме:
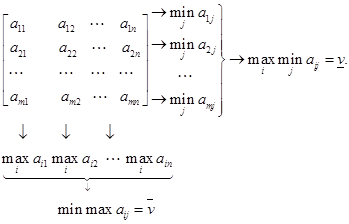
Пример 1. Рассмотрим игру  с матрицей
с матрицей
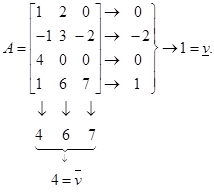
Нижнее значение игры 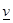 равно 1, верхнее значение
равно 1, верхнее значение  равно 4. Максиминная стратегия
равно 4. Максиминная стратегия
1-го игрока есть  = 4, минимаксная стратегия 2-го игрока есть
= 4, минимаксная стратегия 2-го игрока есть 
Пример 2. Проблема полковника Блотто

Здесь 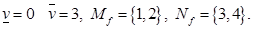
Максиминная стратегия 1-го игрока есть 1 или 2, минимаксная стратегия 2-го игрока есть 3 или 4.
3. Матричные игры с седловыми точками
Рассмотрим матричную игру  , в которой
, в которой

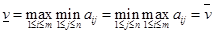
Равенство (43 возможно в том и только том случае, когда матрица A имеет седловую точку. Все множество седловых точек представляет собой прямое произведение 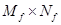 , где
, где 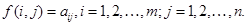
Пусть  – одна из точек этого множества, т. е для любых
– одна из точек этого множества, т. е для любых 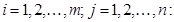

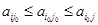
что означает, что элемент 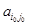 является наибольшим в столбце и наименьшим в строке.
является наибольшим в столбце и наименьшим в строке.
Первый игрок, применяя максиминную стратегию  , гарантирует, что он выиграет не меньше, чем
, гарантирует, что он выиграет не меньше, чем  Второй игрок, применяя минимаксную стратегию
Второй игрок, применяя минимаксную стратегию 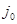 , гарантирует, что больше, чем это же значение v, он не проиграет. Более того, если 1-й игрок применяет стратегию
, гарантирует, что больше, чем это же значение v, он не проиграет. Более того, если 1-й игрок применяет стратегию  , то ввиду правой части неравенства (44) 2-му игроку не выгодно отклоняться от стратегии
, то ввиду правой части неравенства (44) 2-му игроку не выгодно отклоняться от стратегии 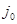 , так как это может увеличить его проигрыш и, наоборот, если 2-й игрок применяет стратегию
, так как это может увеличить его проигрыш и, наоборот, если 2-й игрок применяет стратегию 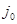 , то ввиду левой части неравенства (44)
, то ввиду левой части неравенства (44)
1-му игроку не выгодно отклоняться от стратегии  , так как это может уменьшить его выигрыш. Таким образом, ситуация (
, так как это может уменьшить его выигрыш. Таким образом, ситуация (  ,
, 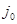 ) является равновесной ситуацией, от которой не выгодно отклоняться каждому из игроков.
) является равновесной ситуацией, от которой не выгодно отклоняться каждому из игроков.
Определение. Ситуация (  ,
, 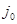 ) называется ситуацией равновесия в чистых стратегиях в игре
) называется ситуацией равновесия в чистых стратегиях в игре  ; стратегии
; стратегии  ,
, 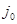 , называются оптимальными стратегиями соответственно 1-го и 2-го игроков; величина
, называются оптимальными стратегиями соответственно 1-го и 2-го игроков; величина
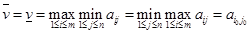
называется значением игры  и обычно обозначается
и обычно обозначается 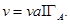
Игра, в которой матрица имеет седловую точку и, значит, существует ситуация равновесия в чистых стратегиях, называется вполне определенной (смысл термина «чистые стратегии» будет ясен из дальнейшего). Во вполне определенной игре нет смысла скрывать свои действия от противника, так как его знание вашей оптимальной стратегии не может увеличить его выигрыш. Заметим также, что поскольку матрица может иметь несколько седловых точек, то у каждого игрока, вообще говоря, может быть по нескольку оптимальных стратегий, которые он может применять по своему усмотрению, не изменяя при этом значения игры (см. формулу 24).
Пример.
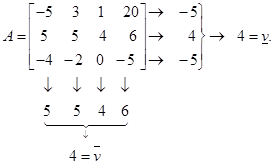
Значение игры  оптимальная стратегия 1-го игрока
оптимальная стратегия 1-го игрока 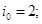
оптимальная стратегия 2-го игрока 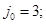 элемент матрицы 4 является наибольшим в третьем столбце и наименьшим во второй строке.
элемент матрицы 4 является наибольшим в третьем столбце и наименьшим во второй строке.
4. Смешанное расширение игры
Если матрица не имеет седловой точки, т. е

то ситуация резко отличается от рассмотренной в предыдущем параграфе. Обратимся к примеру 1 из §2. Максиминной стратегией 1-го игрока является четвертая строка. Если он действительно решил приме
|
|
|


