 |
9.2. Диагональные игры. 9.3. Симметричные игры.
|
|
|
|
9. 2. Диагональные игры
Диагональной называется игра, в которой матрица имеет вид

Где  для всех i = 1, 2, …, n.
для всех i = 1, 2, …, n.
Диагональная игра может рассматриваться как следующая игра поиска. Имеется n коробок. Игрок 2 выбирает одну из коробок и прячет в ней некоторый предмет стоимостью а. Номер выбранной коробки есть номер стратегии 2-го игрока. Этот номер, разумеется, 1-му игроку не сообщается. Затем 1-й игрок выбирает одну из этих n коробок и проверяет, есть ли там предмет. Номер выбранной ячейки есть номер стратегии 1-го игрока. Если в коробке нет предмета, то выигрыш первого игрока равен нулю.
Если в коробке есть предмет, то 1-й игрок получает часть стоимости предмета  - заданные числа.
- заданные числа.
Покажем, что значение диагональной игры положительно. Возьмем стратегию первого игрока  .
.
Тогда для всех 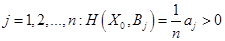 .
.
По лемме 2 (третье замечание к лемме), для любого  , в том числе для оптимальной стратегии
, в том числе для оптимальной стратегии  .
.
Но поскольку  , то
, то
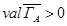 . (92)
. (92)
Теперь покажем, что все стратегии 1-го игрока – активные, т. е., если  - оптимальная стратегия игрока, то
- оптимальная стратегия игрока, то 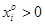 для всех I = 1, 2, …, n.
для всех I = 1, 2, …, n.
9. 3. Симметричные игры.
Напомним, что квадратная матрица А называется кососимметрической, если
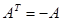 .
.
Матричная игра с кососимметрической матрицей выигрыша называется симметричной.
Теорема 12. В симметричной игре  множества оптимальных стратегий игроков
множества оптимальных стратегий игроков  ,
, 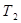 совпадают и значение игры равно нулю.
совпадают и значение игры равно нулю.
10. Итеративный метод решения матричных игр.
В этом параграфе описан весьма наглядный и простой метод приближённого решения матричных игр, известный как метод Брауна-Робинсона или метод фиктивного разыгрывания. Подчеркнём, что в действительности игра не проводится и с помощью фиктивного (мысленного) разыгрывания игроки пытаются найти её решение.
|
|
|
И так, пусть разыгрывается игра  с (m × n)-матрицей
с (m × n)-матрицей 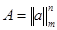 . В первой (фиктивной) партии игроки выбирают свой чистые стратегии совершенно произвольно.
. В первой (фиктивной) партии игроки выбирают свой чистые стратегии совершенно произвольно.
Пусть в первых k фиктивных партиях 1-й игрок свою i-ю чистую стратегию  раз, а 2-й игрок свою j-ю чистую стратегию
раз, а 2-й игрок свою j-ю чистую стратегию 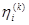 раз.
раз.
Кроме того, обозначим  ,
,  , i = 1, 2, …, m; j = 1, 2, …, n.
, i = 1, 2, …, m; j = 1, 2, …, n.
Очевидно, что для всех i = 1, 2, …, m; j = 1, 2, …, n и любого k = 1, 2, ….
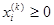 ,
, 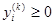 ,
, 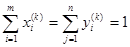 (99)
(99)
Формулы (99) показывают, что векторы  , …,
, …, 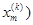 ,
,
 , …,
, …,  являются смешанными стратегиями игроков для любого k = 1, 2, …
являются смешанными стратегиями игроков для любого k = 1, 2, …
В (k + 1)-й партии 1-й игрок выбирает чистую стратегию 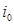 так, чтобы
так, чтобы
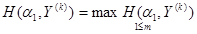 , 100)
, 100)
или в развёрнутом виде

Второй игрок в (k + 1)-й партии выбирает чистую стратегию  так, чтобы
так, чтобы
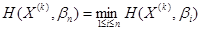 (101)
(101)
Таким образом, получаем некий итерационный процесс, в котором для каждого
k = 1, 2, … определены стратегии 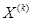 ,
, 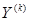 и величины
и величины
 ,
, 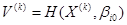 (102)
(102)
Покажем, что для любого k:
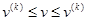 , (103)
, (103)
Где v – значение игры  .
.
Действительно, пусть  - оптимальная стратегия 2-го игрока. Тогда
- оптимальная стратегия 2-го игрока. Тогда 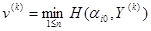 = (см. лемму 3) =
= (см. лемму 3) =  .
.
Левая часть неравенства (103) доказана. Правая часть доказывается аналогично.
Поскольку (103) верно для любого k, то после разыгрывания N партий можем написать:
 (104)
(104)
Иначе говоря, после N партий может быть найдено приближенное значение игры, лежащее в промежутке:
 . (105)
. (105)
Доказывается, (см. [21], с. 110), что
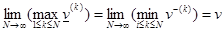 .
.
Таким образом, указанным способом значение игры может быть найдено с любой степенью точности.
Если 1-й игрок имеет единственную оптимальную стратегию, то эта последовательность может не иметь предела. Однако любая ее сходящаяся последовательность сходится к одной из оптимальных стратегий 1-го игрока. То же верно для последовательности стратегий  ,
, 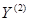 , ...,
, ...,  , … 2-го игрока.
, … 2-го игрока.
Достоинством метода является простота его реализации.
К недостаткам метода относится его медленная и, главное, немонотонная сходимость. Длина промежутка (105) убывает со скоростью, пропорциональной
|
|
|
 .
.
Для симметричных игр оценка скорости сходимости может быть улучшена (см. [21], с. 118) до 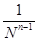 .
.
11. Матричные игры и линейное программирование.
Решение матричной игры может быть сведено к задаче линейного программирования.
Сначала будем считать, что все элементы матрицы игры  строго положительны. Рассмотрим задачу линейного программирования
строго положительны. Рассмотрим задачу линейного программирования
 (106)
(106)
И двойную задачу
 (107)
(107)
Из теоремы двойственности следует, что обе задачи (106), (107) имеют оптимальное решение
 ,
,
такое, что
 .
.
Покажем, что векторы
 ,
, 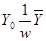
Являются оптимальными стратегиями игроков, а 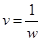 - значение игры
- значение игры  .
.
Так как все координаты векторов  ,
, 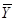 неотрицательны и
неотрицательны и  , то координаты векторов
, то координаты векторов 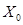 ,
,  неотрицательны. Следовательно,
неотрицательны. Следовательно,

А также
 .
.
Таким образом, 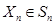 ,
,  .
.
Далее имеем
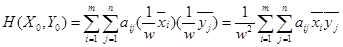 . (108)
. (108)
С другой стороны, из (106), (107) следует, что
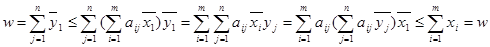
Таким образом,
 ,
,
и из (108) получаем, что
 (109)
(109)
Пусть  ,
,  - произвольные стратегии игроков. Тогда
- произвольные стратегии игроков. Тогда

 , (110)
, (110)
Формулы (109), (110) показывают, что
 .
.
Следовательно, 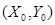 - ситуация равновесия в игре
- ситуация равновесия в игре  и (109) ее значение.
и (109) ее значение.
Если не все элементы матрицы А положительны, то можно ко всем ее элементам добавить достаточно большое число b так, чтобы 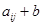 было положительным для всех i = 1, 2, …, n, и при этом получается игра с матрицей
было положительным для всех i = 1, 2, …, n, и при этом получается игра с матрицей  , стратегически эквивалентной исходной (см. §6). Оптимальные стратегии игроков в этих играх одинаковы, и если
, стратегически эквивалентной исходной (см. §6). Оптимальные стратегии игроков в этих играх одинаковы, и если
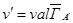 ,
,
то 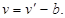
Сведение решения матричной игры в задаче линейного программирования позволяет использовать любой метод решения задач линейного программирования для решения матричных игр, например, симплекс-метод.
КООПЕРАТИВНЫЕ ИГРЫ
1. Смешанное расширение бескоалиционной игры
Замена в бесконечной игре 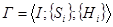 множества
множества  стратегий игрока i множеством
стратегий игрока i множеством  - распределением вероятностей (см. §4 раздела «Матричные игры») даст смешанное расширение игры
- распределением вероятностей (см. §4 раздела «Матричные игры») даст смешанное расширение игры  . Средний выигрыш игрока i равен
. Средний выигрыш игрока i равен 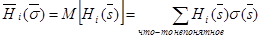 , где
, где 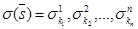 - вероятность ситуации
- вероятность ситуации  .
.  .
.
Обозначим через  - средний выигрыш игрока i при выборе игроком i стратегии
- средний выигрыш игрока i при выборе игроком i стратегии  . Тогда из
. Тогда из  ,
, 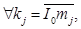 следует
следует 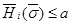 .
.
Лемма 1. 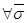 ,
,  :
:  ,
, 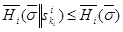 .
.
Определение 1. Ситуация  называется ситуацией равновесия, если для любого игрока i и любой его смешанной стратегии
называется ситуацией равновесия, если для любого игрока i и любой его смешанной стратегии  имеет место неравенство
имеет место неравенство 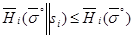 .
.
|
|
|
Теорема 1. Ситуация  называется ситуацией равновесия тогда и только тогда, когда для любого игрока i и любой его чистой стратегии
называется ситуацией равновесия тогда и только тогда, когда для любого игрока i и любой его чистой стратегии 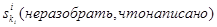 выполняется неравенство
выполняется неравенство  .
.
Теорема 2 (теорема Ноша). В каждой бескоалиционной игре Г существует ситуация равновесия в смешанных стратегиях.
2. Биматричные игры
 - биматричная игра, т. е. игра двух лиц, каждое из которых обладает набором стратегий
- биматричная игра, т. е. игра двух лиц, каждое из которых обладает набором стратегий  и
и  соответственно. В дальнейшем для краткости будем обозначать биматричную игру
соответственно. В дальнейшем для краткости будем обозначать биматричную игру  .
.
Решение 2× 2 биматричной игры. Пусть каждый из игроков располагает двумя стратегиями (m=n=2). Следовательно
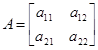 ;
;  - 2× 2 матрицы. Смешанные стратегии игроков 1 и 2 соответственно равны
- 2× 2 матрицы. Смешанные стратегии игроков 1 и 2 соответственно равны 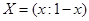 и
и 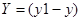 ,
,  . Находят средний выигрыш по формулам
. Находят средний выигрыш по формулам
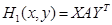 ;
;  ,
,
Получаем выражения:
 ,
,
 .
.
Ситуация (x, y) Является приемлемой для игрока 1, если

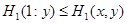
Одновременная реализация этих двух условий приводит к системе
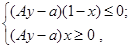
Где 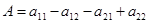 ;
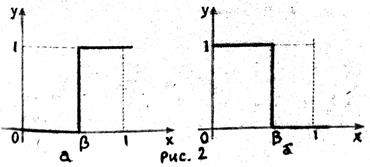
;  . Решение системы на координатной плоскости x, y изображено на рис. 1, а, б.
. Решение системы на координатной плоскости x, y изображено на рис. 1, а, б.
 На рис. 1
На рис. 1  - вероятность первой стратегии игрока 2. Для наглядности принято:
- вероятность первой стратегии игрока 2. Для наглядности принято:  .
.
Потребовав, чтобы ситуация (x; y) была приемлемой и для игрока 2, получим 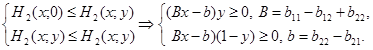
Решение системы изображено на рис. 2, а, б; 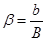 - вероятность первой стратеги игрока 1. В ситуациях, когда
- вероятность первой стратеги игрока 1. В ситуациях, когда 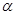 (или
(или 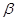 ) не принадлежат отрезку [0, 1], решением является прямая – одна из сторон единичного квадрата. В тех же ситуациях, когда
) не принадлежат отрезку [0, 1], решением является прямая – одна из сторон единичного квадрата. В тех же ситуациях, когда 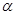 (
( 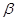 ) принадлежит указанному отрезку, этот параметр определяет y (x), т. е. смешанную стратегию противника.
) принадлежит указанному отрезку, этот параметр определяет y (x), т. е. смешанную стратегию противника.
Примеры 1 «Дилемма бандита». [15] (Сравнение с примером 6 введения. ) В предварительном заключении находятся два преступника (игрок 1 и 2), подозреваемые в совершении тяжкого преступления. Каждый из них имеет две стратегии: 1 – сознаться, 2 – не сознаваться. Если оба сознаются, то будут осуждены на длительный срок (например, 8 лет). Если оба не сознаются, то обвинение в тяжком преступлении будет снято, но каждого из них смогут осудить на незначительный срок (например, 1 год). В случае же, кода сознается лишь один, о будет освобождён, а его упорствующий партнёр будет осуждён, например, на 10 лет. Матрицы выигрышей в рассматриваемой игре равны:
|
|
|
 ;
;  .
.
 Кривые приемлемых ситуаций для игроков 1 и 2 [соответственно линии (1) и (2)] изображены на рис. 3. Имеется единственная точка пересечения (1; 1), т. е. единственная ситуация равновесия, когда каждый из игроков выбирает первую стратегию и теряет 8. Несмотря на то, что в ситуации (0; 0) каждый из них теряет лишь 1, эта ситуация является неустойчивой. Каждый игрок, изменяя свою стратегию (при неизменной стратегии другого), может увеличить свой выигрыш (с -1 до 0).
Кривые приемлемых ситуаций для игроков 1 и 2 [соответственно линии (1) и (2)] изображены на рис. 3. Имеется единственная точка пересечения (1; 1), т. е. единственная ситуация равновесия, когда каждый из игроков выбирает первую стратегию и теряет 8. Несмотря на то, что в ситуации (0; 0) каждый из них теряет лишь 1, эта ситуация является неустойчивой. Каждый игрок, изменяя свою стратегию (при неизменной стратегии другого), может увеличить свой выигрыш (с -1 до 0).
2. «Семейный спор» (пример 5 введения). Два партнера договариваются о совместно проводимых ими действиях 1 или 2. В случае совместного проведения действия 1 (выбор стратегии 1) первый игрок получает выигрыш 1, второй – 2. В случае совместного осуществления действия 2 первый игрок получает выигрыш 2, а второй – 1. При выполнении различных действий выигрыш каждого равен 0. Таким образом, матрицы выигрышей равны:
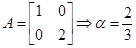 ;
;  .
.
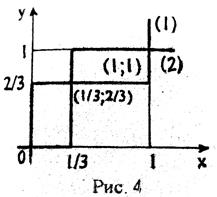
Кривые приемлемых ситуаций (1) и (2) представлены на рис. 4, из рассмотрения которого следует, что игра имеет три ситуации равновесия:
-(0; 0) и (1; 1), соответствующие выбору игроками 1 и 2 второй и первой стратегии (чистых) одновременно;
- 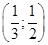 , соответствующая реализации игроками смешанных стратегий. Первые две ситуации характеризуются различными в каждой из них выигрышами игроков.
, соответствующая реализации игроками смешанных стратегий. Первые две ситуации характеризуются различными в каждой из них выигрышами игроков.
В третьей ситуации, как легко убедиться,  .
.
3. Характеристическая функция кооперативной игры
Любое подмножество множества игроков 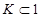 называется коалицией. Объединяясь в коалицию, игроки получают более богатый выбор стратегий и, как следствие, потенциально больший суммарный выигрыш. Очевидно, коалиция K оказывается в наихудшей ситуации, когда остальные игроки объединяются в антикоалицию 1\K и координируют свои действия с целью получения наибольшего выигрыша. Характеристической функцией
называется коалицией. Объединяясь в коалицию, игроки получают более богатый выбор стратегий и, как следствие, потенциально больший суммарный выигрыш. Очевидно, коалиция K оказывается в наихудшей ситуации, когда остальные игроки объединяются в антикоалицию 1\K и координируют свои действия с целью получения наибольшего выигрыша. Характеристической функцией  называется наибольший гарантированно получаемый коалицией K выигрыш в условиях противодействия со стороны антикоалиции.
называется наибольший гарантированно получаемый коалицией K выигрыш в условиях противодействия со стороны антикоалиции.
Примеры. 1. Игра с главным игроком. В игре участвуют n игроков из которых один (например, игрок a ) – главный. Коалиция K выигрывает 1, если она содержит главного игрока и еще хотя-бы одного из всех n-1 остальных («неглавных»):

2. «Помещик и батраки». В игре участвуют игроки 1; 2; …; n-1 – батраки и игрок n – помещик. Помещик, наняв k бараков, может получить доход f(k), а батраки в любом случае сами по себе (без помещика) дохода получить не могут.

3. В игре участвуют три игрока: 1, 2, 3, располагающие каждый тремя стратегиями соответственно: 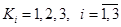 Всего такая игра имеет 27 ситуаций, выигрыши в которых сведены в три таблицы, содержащие значения (
Всего такая игра имеет 27 ситуаций, выигрыши в которых сведены в три таблицы, содержащие значения ( 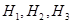 ).
).
|
|
|
 =1 =1
|  =2 =2
| ||
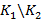
| 1 2 3 | 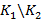
| 1 2 3 |
| (2; 1; -3)(3; 0; -3)(4; 1; -5) | (3; 1; -4)(3; 2; -5)(5; 0; -5) | ||
| (-1; -2; 3)(-1; 3; -2)(-2; -2; 4) | (-1; 2; -1)(-1; 3; -2)(-2; 1; 1) | ||
| (-2; 1; 1)(-1; 2; -1)(-2; 0; 2) | (0; 2; -2)(0; 3; -3)(-1; -2; 3) | ||
 =3 =3
| |||
| 1 2 3 | ||
| (4; 1; -5)(4; 2; -6)(5; 2; -7) | |||
| (-1; 3; -2)(-1; 4; -3)(-2; 2; 0) | |||
| (-2; -1; 3)(-2; 0; 2)(-3; -1; 4) | |||
Возможны коалиции: 
Подробно рассмотрим коалиции, объединяющие двух игроков. Каждая такая коалиция обладает 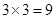 стратегиями и, реализуя совместно каждую из них, получает суммарный выигрыш, значения которого приведены в следующих таблицах.
стратегиями и, реализуя совместно каждую из них, получает суммарный выигрыш, значения которого приведены в следующих таблицах.
| {2, 3} против {1} | {1, 3} против {2} | ||||||

| 
| ||||||
| (1, 1) | -2 | +1 | +2 | (1, 1) | -1 | -1 | |
| (1, 2) | -3 | +1 | (1, 2) | -1 | -2 | ||
| (1, 3) | -4 | +1 | +2 | (1, 3) | -1 | -2 | -2 |
| (2, 1) | -3 | +1 | +1 | (2, 1) | -3 | ||
| (2, 2) | -3 | +1 | (2, 2) | -2 | -3 | -1 | |
| (2, 3) | -4 | +1 | +2 | (2, 3) | -3 | -4 | -2 |
| (3, 1) | -4 | +2 | +2 | (3, 1) | -1 | -2 | |
| (3, 2) | -5 | +2 | +1 | (3, 2) | -2 | -3 | -2 |
| (3, 3) | -5 | +2 | +3 | (3, 3) | |||
| {1, 2} против {3} | |||||||

| |||||||
| (1, 1) | |||||||
| (1, 2) | |||||||
| (1, 3) | |||||||
| (2, 1) | -3 | ||||||
| (2, 2) | |||||||
| (2, 3) | -4 | -1 | |||||
| (3, 1) | -1 | ||||||
| (3, 2) | -2 | ||||||
| (3, 3) | -2 | -3 | -4 | ||||
Так как каждая из этих трех таблиц описывает матричную игру, то легко найти её решение (см. §3 раздела «Матричные игры»), которое выделено в каждой из таблиц штриховкой. Таким образом,  Так как рассматривается игра с нулевой суммой, то
Так как рассматривается игра с нулевой суммой, то 
Система  называется классической кооперативной игрой.
называется классической кооперативной игрой.
|
|
|


