 |
С-ядро в общей игре третьих лиц
|
|
|
|
С-ядро в общей игре третьих лиц
Рассматривая игру в 0-1-редуцированной форме, имеем для коалиций из двух игроков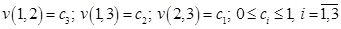 
. Следуя необходимому и достаточному условию принадлежности дележа С-ядру, получаем для компонентов дележа следующую систему неравенств: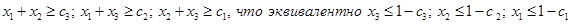 
Почленное сложение трех неравенств дает
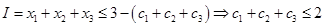- необходимое условие существования
С-ядра.
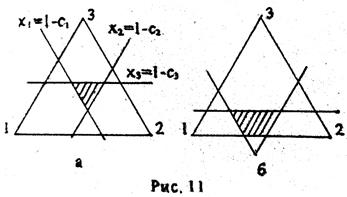Графическое изображение С-ядра представлено на рис. 11. В ситуации а все точки попарных пересечений прямых 
лежат в треугольнике 1, 2, 3. В ситуации б точки пересечения ; лежат за пределами этого треугольника и имеют координату 
. Отсюда 
- условие выхода этой вершины за пределы треугольника. Такую же роль играют неравенства 
для двух остальных вершин.
8. Решение кооперативной игры по Нейману-Моргенштерну
Решением по Нейману-Моргенштерну (Н-М решением) называется множество дележей R, удовлетворяющее условиям:
1)никакие два дележа из R не доминируют друг над другом;
2) 
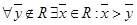
Эти два условия носят название условий соответственно внутренней и внешней устойчивости. Первое означает невозможность противопоставления двух дележей из R ни одной из коалиций. Второе – существование коалиции, стремящейся заменить дележ, не принадлежащий R, на дележ R (т. е. восстановить равновесие).
Свойства Н-М решения
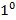. Если 
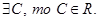Справедливость этого свойства вытекает из того, что если 
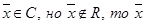- доминируемый дележ. Противоречие.
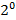. Если R состоит из единственного дележа, то игра – несущественна. Так как если 
- дележ игры в 0-1-редуцированной форме, то 
и может быть построен дележ 
, который не доминируется над дележом
(проверить! ). Следовательно, и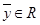 
Н-М решение в игре трех лиц с постоянной суммой
Так как не доминирующие друг на другом два дележа лежат на прямой, параллельной
|
|
|
одной из сторон треугольника дележей 1, 2, 3, то возможны две ситуации (рис. 12):
а) все 
лежат на одной прямой (на рис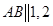 
)
б) дележи 
не лежат на одной прямой (легко убедиться, что это возможно лишь, если R = {A, B, C}, где A, B, C – середины соответствующих сторон треугольника) В ситуации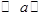 
дележ 
доминирует все дележи параллелограмма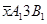 
по коалиции (1, 2), а все точки отрезка AB – дележи треугольника А3В. По коалиции (1, 3) дележ 
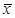доминирует дележи параллелограмма 
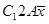, а все дележи отрезка АВ – дележи параллелограмма 
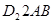. По коалиции (2, 3) дележ 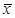доминирует дележи параллелограмма 
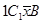. Из рассмотрения рис. 12, а следует: для того чтобы дележи отрезка АВ доминировали все дележи трапеции 12АВ, необходимо и достаточно, чтобы точка пересечения прямых 
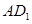и 
находилась ниже стороны 1, 2 (координата 
этой точки была отрицательна). Так как на прямой АВ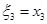 
, те координаты концов отрезка АВ: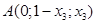 
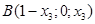. Следовательно, уравнение прямой 
; прямой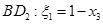 
. Условие 
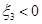эквивалентно 
– отрезок АВ лежит ниже средней линии треугольника. Поэтому 
. Такое решение называется дискриминирующим (игрока 3). Точно так же строятся Н-М-решения, дискриминирующие игроков 1 или 2.
В примере 3 раздела 3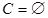 
(игра с постоянной суммой). Для построения R воспользуемся результатом, полученным для игры в 0-1-редуцированной форме (см. раздел 5) осуществляется по формуле 
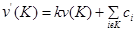, где 
. Подставив в эти формулы параметры рассматриваемого примера v(1) = 2; v(2) = 0; v(3) = -5; v(1, 2, 3) = 0, получим 
. Поэтому дележ игры 
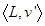связав с дележом исходной игры формулами: 
; 
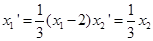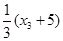Использование этих формул даёт возможность найти дележи Н-М-решения, дискриминирующего, например, игрока 2: 
9. Виктор Шепли
Игрок I в кооперативной игре 
называется болваном, если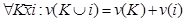 
Очевидно, болван – это игрок, не способный улучшить свойства коалиции, а лишь механически добавляющий к выигрышу уже существующей коалиции свой гарантированно получаемый выиграть.
|
|
|
Множество игроков не являющихся болванами в данной игре, называется носителем игры. Если N – носитель игры, то
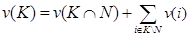
Сформулируем требования, которые позволили бы найти единственный несправедливый, с точки зрения этих требований, дележ в виде аксиом
Аксиома эффективности: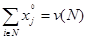 
То есть общий выигрыш носителя распределяется между его участниками
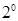Аксиома симметрии: 
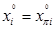где 
номер игрока i после перестановки игроков данной игры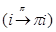 
, удовлетворяющей свойству автоморфизма характеристической функции: 
, где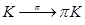 
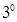Аксиома агрегации: есл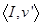и 
и 
– две игры с одним и тем же множеством игроков, то для игры 
Ниже будет доказано, что система этих трех аксиом является полной и непротиворечивой, т. е. для любой характеристической функции v существует единственный дележ 
, удовлетворяющий трём приведенным выше аксиомам.
Дележ называется вектором Шепли
|
|
|
