 |
Вектором Шепли и простейшая игра
|
|
|
|
Вектором Шепли и простейшая игра
Игра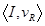 
называется простейшей если 
Таким образом, в простейшей игре коалиция К выигрывает, если она содержит некоторую минимальную выигрывающую коалицию R(т. е. R – носитель игры). Вектор Шепли для игры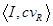 
(с > 0) определяется из системы сформулированных выше аксиом:
Аксиома эффективности: 
Аксиома симметрии: 
Для игроков не входящих в 
Лемма Для любой игры существует её единственное линейное представление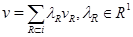 
Построение вектора Шепли. Воспользовавшись линейным представлением характеристической функции игры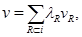 
для каждой из компонент вектора Шепли получим 
Подставив формулы для 
и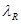 
из предыдущего раздела, получим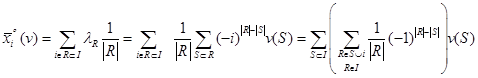 
Введем обозначение 
Если, 
то
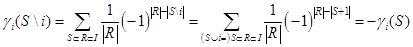
В результате
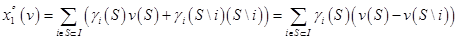
Для всех S, содержащих 
,
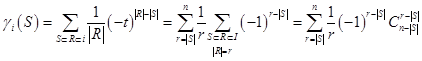
Вычисление последней суммы потребует ряда вспомогательных вычислений:
Интеграл I(n, t) находим, интегрируя по частям:
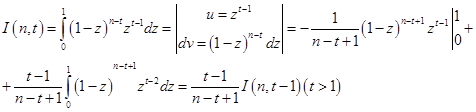
Следовательно,
Так как 
(проверить самостоятельно). Таким образом, 
, откуда
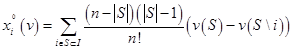
Замечание. Если все перестановки игроков равновероятностные, то вероятность каждой из них равна 
. Обозначим через 
множество игроков, предшествующих игроку i в данной перестановке. Тогда 
представляет собой приращение гарантированного выигрыша коалиции при присоединении к ней игрока i. Найдём математическое ожидание этого приращения в условиях равновероятности всех перестановок: 
Так как число перестановок, в которых игроку i предшествуют игроки из S и только они, равно 
, то вероятность появления такой перестановки равна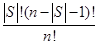 
.
Следовательно,
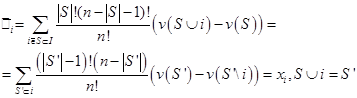
Таким образом i-я компонента вектора Шепли равна среднему приращению, получаемому предшествующей в перестановке коалицией от присоединения игрока i.
|
|
|
Полученный результат можно интегрировать следующим образом: игроки по очереди в случайном порядке включаются в игру; игрок i получает ту сумму, на которую его приход увеличивает выигрыш уже собравшейся коалиции. Математическое ожидание этой суммы и равно соответствующей компоненте вектора Шепли.
Примеры
1. Игра с главным игроком. Главный игрок (игрок n) увеличивает выигрыш любой предшествующей коалиции, если оказывается в ней не первым и не последним. Вероятность этого события равна 
. Следовательно,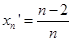 
. Все остальные (неглавные) игроки равноправны. Поэтому 
. В данной игре отношение выигрышей главного и рядового игроков равно
2. Помещик и батраки. Помещик (игрок n) с вероятностью, равной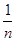 
, окажется на любом месте (с номером k) и увеличит тем самым значение характеристической функции на f(k - 1). Поэтому 
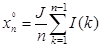. На долю всех остальных игроков (батраков) остаётся 
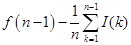. Поэтому из условия равноправия батраков получаем 
3. В примере 3 найдена характеристическая функция. Найдём компоненты вектора Шепли. Так, игрок 1 может отказаться на каждом из трёх возможных мест с вероятностью 
. Если он оказывается на первом месте, 
. Если на втором, то с вероятностью 
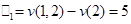или 
. Наконец, оказываясь на третьем месте, он присоединяется к коалиции (2, 3) и, следовательно, 
. Отсюда 
.
Расчет для игрока 2 оформим по-другому. Запишем 3! = 6 возможных перестановок трёх игроков; (2; 1; 3); (2; 3; 1); (1; 2; 3); (3; 2; 1); (1; 3; 2); (3; 1; 2).
Вероятность каждой из них равна 
. Вычислим для них значения 
Для первой и второй: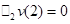 
Для третьей: 
Для четвертой: 
Для пятой и шестой: 
Следовательно, 
. Самостоятельно убедиться, что 
. Таким образом, вектор Шепли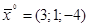 
|
|
|
