 |
Элементарные сведения из теории вероятностей
|
|
|
|
Элементарные сведения из теории вероятностей
Пусть в результате некоторого опыта происходит одно и только одно из событий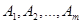 
. Предсказать появления какого-либо конкретного события 
на основании предыдущего опыта наблюдателя невозможно. Однако известно, что некоторые события появляются объективно чаще, чем другие. Для того чтобы количественно характеризовать степень уверенности объективного наблюдателя в том что данное событие произойдет, используется функция 
– вероятность события , обладающая следующими свойствами:
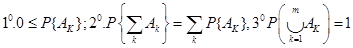
Здесь символ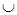 
используется в обычном теоретико-множественном смысле 
- происходит или событие 
, или событие 
. Событие 
– достоверное событие (событие, которое обязательно происходит). 
– невозможное событие. Наиболее просто расчетные соотношения выглядит, когда исходы опыта обладают свойством симметрии и поэтому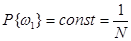 
. В этом случае событие А можно рассматривать как объединение влекущих его элементарных исходов 
, что приводит к формуле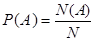 
, где N(A) – число элементарных исходов, благоприятствующих событию А.
Пример. Колесо рулетки разделено на 360 перенумерованных секторов с центральным углом 
. Красное поле содержит секторов, черное – N, а белое - 
. Колесо приводится во вращение и останавливается в случайном положении. Вероятности выпадения красного, черного и белого равны соответственно: 
.
Если каждому из событий 
поставлено в соответствие число: 
, то говорят что задана дискретная случайная величина 
с возможными значениями 
.
Вероятности 
, образуют ряд распределения с очевидными свойствами: 
. В рассмотренном выше примере каждому из трёх полей можно поставить в соответствие число, построив, таким образом, простейшую модель дискретной случайной величины.
|
|
|
Для того чтобы характеризовать среднее ожидаемое значение случайной величины, используется числовая характеристика (неслучайная) – математическое ожидание 
со следующими легко проверяемыми свойствами:
Аналогично 
В пособии используется случайная величина, принимающая лишь натуральные значения (номера чистых стратегий), а также случайная величина, значения которой равны выигрышу игрока в той или иной ситуации игры. Так как ситуация в игре определяется стратегиями всех её участников, то для её описания используется многомерная случайная величина 
со значениями 
, вероятности которых определяются правилом умножения вероятностей: . Математическое ожидание в этом случае вычисляется по формуле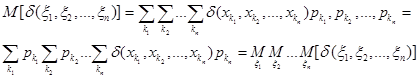 
представляющей собой суперпозицию операторов 
, обладающую свойством коммутативности.
Лемма. Если 
, то либо 
(неслучайная величина), либо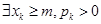 
.
Библиографический список
1. Вентцель Е. С. Элементы теории игр. М.: Физматгиз, 1961.
2. Вилкас Э. И. Оптимальности в играх и решениях. М.: Наука 1990.
3. Вильямс Д. Д. Совершенный стратег или …. М.: Сов. радио, 1960.
4. Волгин Л. Н. Принцип согласованного оптимума. М.: Сов. радио, 1977
5. Воробьев Н. Н. Современное состояние теории игр //Первая всесоюзная конф. По теории игр Ереван, 1968.
6. Воробьев Н. Н. Теории игр. Лекции для экономистов-кибернетиков. Изд-во ЛГУ. 1974.
7. Воробьев Н. Н. Теории игр. М.: Знание 1976.
8. Воробьев Н. Н. Основы теории игр. Бескоалиционные игры. М.: Наука 1981
9. Дрешер М. Стратегические игры. Теория и приложения. М.: Сов. радио, 1984.
10. Дюбин Г. Н., Суздаль В. Г. Введение в прикладную теорию игр. М.: Наука 1981.
11. Карлин С. Математические методы в теории игр, программирования и экономике М.: Мир 1964.
12. Костевич Л. С., Лалко А. А. Теория игр. Иследование операций. Минск: Вышейная школа, 1982
|
|
|
13. Льюе Р. Д., Райфа Х. Игры и решения. М.: ИИЛ, 1961.
14. Мак-Кинси Д. Введение в теорию игр. Физматгиз, 1959.
15. Мулен, Эрве. Теория игр с примерами из математической экономики М.: Мир 1985
16. Оуен Г. Теория игр М.: Мир 1971
17. Дж. Фон Нейман, Моргенштерн О. Теория игр и экономическое поведение М.: Наука 1970
18. Петросян Л. А. и др. Теория игр. М.: Высшая школа, 1998
19. Матричные игры. Сборник статей. М.: Физматгиз, 1961
|
|
|
