 |
Свойства характеристической функции
|
|
|
|
Свойства характеристической функции
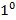. Персональность: 
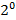. Супераддитивность: 
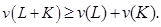т. е. объединение в коалицию дает дополнительные преимущества.
. Дополнительность: для игры с постоянной суммой 
.
4. Дележи в кооперативной игре
Необходимость распределения выигрыша коалиции между её членами приводит к понятию дележа, т. е. вектора 
описывающего выигрыши всех участников игры.
Свойства дележа
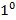. Свойство индивидуальной рациональности: 
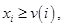т. е., вступая в коалицию, любой участник игры рассчитывает получить больше, чем мог бы выиграть индивидуально.
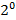. Свойство коллективной (групповой) рациональности: 
т. е. дележ реализует все потенциальные возможности данной игры.
Отсюда следует необходимое и достаточное условие дележа: 
дележ тогда и только тогда, когда 
.
Кооперативная игра 
, для которой свойство супераддитивности вырождается в аддитивность: 
называется несущественной.
Теорема. Для того чтобы игра была несущественной, необходимо и достаточно, чтобы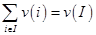 
.
Следствие. В несущественной игре имеется единственный дележ 
5. Стратегическая эквивалентность кооперативных игр
Игра стратегически эквивалентна игре 
Обладая свойствами рефлексивности 
и транзитивности 
, стратегическая эквивалентность является отношением, разбивающим множество кооперативных игр(характеристических функций) на непересекающиеся классы. Если 
, то дележу 
соответствует дележ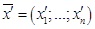 
, где 
.
Если 
нулевой.
Теорема. Любая несущественная игра эквивалентна нулевой игре.
Теорема. Любая существенная кооперативная игра стратегически эквивалентна одной и только одной игре в 0-1 редуцированной форме.
6. Доминирование дележей
Сравнивание дележей с точки зрения выгоды участников коалиции приводит к понятию доминирования дележей: дележ 
доминирует дележ 
по коалиции 
. Если
1) 
. То есть коалиция K отдает предпочтение дележу по сравнению с дележом .
|
|
|
Дележ доминирует дележ 
, если существует коалиция K, по которой доминирует . Это означает, что в данной игре найдется коалиция, которая дележу предпочитает дележ .
Свойства доминирования
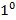. Доминирование невозможно по коалиции из одного игрока, так как в этом случае 
- противоречит индивидуальной рациональности.
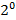. Доминирование невозможно по всему множеству игроков 1, так как 
- противоречит коллективной рациональности.
. Если 
, причем 
. Следовательно, отношения доминирования могут исследоваться для классов стратегической эквивалентности, и изучать их достаточно для несущественных игр по нулевой игре, для несущественных игр по нулевой игре, для существенных – по их 0-1-редуцированной форме.
Доминирование дележей в существенной игре третьих лиц
Рассмотрим 0-1-редуцированную форму игры с постоянной суммой.
Дележ 
обладает свойствами: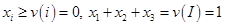 
.
В системе координат 
(рис. 5) множество делений представляет собой двумерный симплекс, который далее будем изображать в виде равностороннего треугольника(рис. 6) Линия 
представляет собой отрезок прямой, проходящей через точку параллельно стороне 1, 2. Увеличение 
приводит к смещению отрезка в сторону вершины 3.
Доминирование 
означает 
. Так как 
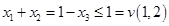, то первое неравенство выполняется автоматически. Область, в которой выполняются остальные два неравенства изображена на рис. 7 и имеет вид параллелограмма. Области доминирования по другим коалициям изображены на рис. 8.
.
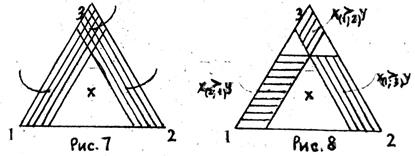
Для того чтобы ни один из двух данных дележей и не доминировал другой необходимо и достаточно, чтобы прямая, проходящая через точки , треугольника 1, 2, 3, была параллельна одной из его сторон.
|
|
|
Отказавшись от условия постоянства суммы, запишем условия доминирования по коалиции (1, 2) в виде:
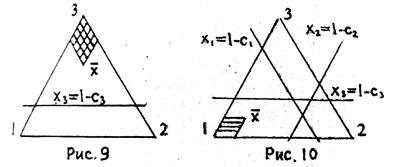
Так как 
, то первое условие может оказать существенное влияние на вид области доминирования (рис. 9). Заменив первое неравенство эквивалентным 
, отметим, что вид области доминирования коалиции (1, 2) не изменится, если прямая 
расположена дальше от вершины 3, чем точка . В противном случае доминирование невозможно, т. е. 
. Так, на рис. 10 изображена ситуация, когда доминирование возможно только по коалиции (2, 3).
7. С-ядро кооперативной игры
Множество дележей, не доминируемых над другими дележами, называется C-ядром кооперативной игры .
Теорема. Для того чтобы 
, необходимо и достаточно, чтобы
(*)
Следствия 1. Для того чтобы , необходимо и достаточно выполнения системы линейных неравенств (*). Отсюда следует, что С-выпуклое множество.
2. В случае несущественной игры единственный дележ совпадает с С-ядром.
3. В существенной игре с постоянной суммой С-ядро пусто. Действительно, если , то 
, тогда как известно, что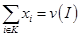 
. Поэтому 
, то есть игра - несущественная.
|
|
|
