 |
Второе начало термодинамики. Второе начало термостатики
|
|
|
|
Второе начало термодинамики
Как отмечалось выше, первое начало термодинамики представляет собой количественное выражение закона сохранения и превращения энергии, оно позволяет составить энергетический баланс исследуемых процессов, но не определяет направление их протекания. Условия осуществления и направленности протекания процессов определяются на основании второго начала термодинамики.
В совокупности первое и второе начало термодинамики являются фундаментом в построении теории тепловых машин и технической термодинамики в целом.
Второе начало классической термодинамики обычно формулируется как объединенный принцип существования и возрастания некоторой функции состояния тел и сложных систем, названной энтропией (термин энтропия предложен Р. Клаузиусом: еn – в, внутрь и trope или tropos – обращение, путь; в целом – обращение внутрь, мера обесценения энергии).
Математическое выражение второго начала классической термодинамики может быть представлено в виде следующего выражения:
.
Н. И. Белоконь справедливо заметил, что принципы существования и возрастании энтропии различны по содержанию и значимости и предложил рассматривать эти принципы раздельно.
Принцип существования энтропии справедлив для равновесных термодинамических систем и распространяется на любые процессы – обратимые и необратимые. Принцип существования энтропии и абсолютной температуры как термодинамических функций состояния равновесных систем, по терминологии проф. Н. И. Белоконь, был назван вторым началом термостатики.
Принцип возрастания энтропии характеризует только наиболее вероятное направление течения реальных процессов и, следовательно, имеет несомненно меньшую область применения, чем принцип существования энтропии. Принцип возрастания энтропии изолированных систем при протекании в них реальных процессов Н. И. Белоконь назвал вторым началом термодинамики.
|
|
|
Второе начало термостатики
В качестве постулата второго начала термостатики используется утверждение, что «температура есть единственная функция состояния, определяющая направление самопроизвольного теплообмена».
Для вывода математического выражения второго начала термостатики рассмотрим адиабатно изолированную систему, состоящую из термически сопряженных тел (рис. 4). Первое тело (I) - любое тело (например,
реальный газ), совершает произвольные процессы - обратимые и необратимые, второе тело (II) - контрольное тело - идеальный газ, совершает обратимый круговой процесс. Оба тела в каждый момент имеют одинаковую
температуру (tI = tII= t).
| Рис. 4.. Адиабатно изолированная система двух термически сопряженных тел |
Первое и второе тело осуществляют разнообразные процессы изменения состояния, к ним извне подводится (или отводится) работа, между телами происходит теплообмен, но для адиабатно изолированной системы выполняется обязательное условие
. (18)
Разделим уравнение (18) на некоторую функцию, зависящую только от температуры t(t). Для идеального газа эта функция равна абсолютной температуре t(tII) = TII. С учетом равенства температур двух тел получаем
. (19)
Так как тела I и II возвращаются в исходное состояние одновременно (согласно теореме теплового равновесия тел в равновесных круговых процессах) последнее уравнение можно интегрировать по замкнутому контуру
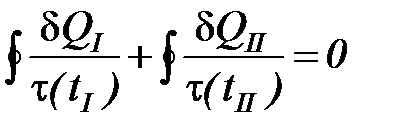. (20)
|
|
|
Второй интеграл по замкнутому контуру для идеального газа, как интеграл функции состояния, равен нулю
. (21)
Поэтому и первый круговой интеграл в уравнении (21) также равен нулю
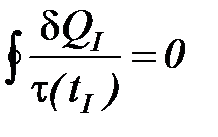. (22)
Если круговой интеграл равен нулю, то это значит, что подынтегральное выражение представляет из себя полный дифференциал некоторой функции состояния, названной энтропией ( 
), а функция t(tI) является интегрирующим делителем
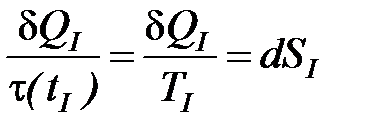. (23)
Так как тело I - любое тело и свойства тел I и II независимы, полученное выражение (23) распространяется на все равновесные процессы изменения состояния любых систем. Выбранная функция t(t), которая не зависит от вида тел, называется абсолютной температурой t(t)= Т, а температурная шкала называется абсолютной термодинамической.
Таким образом, получаем математическое выражение второго начала термостатики - принципа существования энтропии и абсолютной температуры для любых равновесных систем
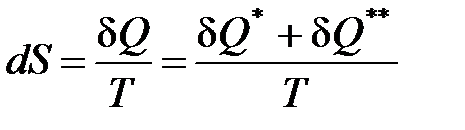(24)
и для 1 кг системы
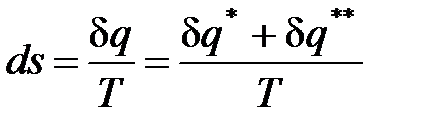. (25)
Второе начало термостатики утверждает принцип существования энтропии и абсолютной температуры как функции состояния любой равновесной термодинамической системы, совершающей обратимые или необратимые процессы.
|
|
|
