 |
Теплообмен при свободной конвекции на горизонтальной стенке
|
|
|
|
Теплообмен при свободной конвекции на горизонтальной стенке
Теплообмен на нагретых горизонтальных плитах в условиях свободной конвекции отличается особой организацией движущейся среды. Над нагретой поверхностью появляется восходящее и нисходящее струйное движение с возможными зонами циркуляции.
У поверхности, обращенной вниз, движение происходит лишь в тонком слое под поверхностью от центра к краям. Большая скорость движения достигается при обтекании краев. Чем больше размер пластины, тем меньше краевой эффект.
Для расчета теплообмена можно воспользоваться следующим уравнением:
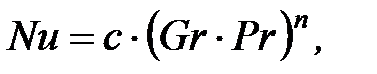(6)
где
при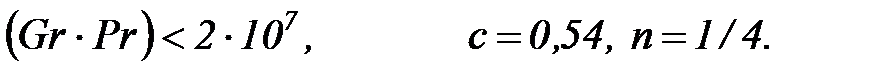 
при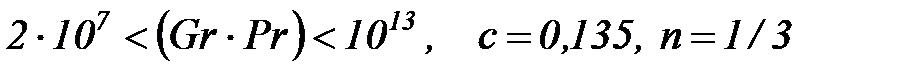 
;
За определяющий линейный размер принимается меньшая сторона, за определяющую температуру – температура пограничного слоя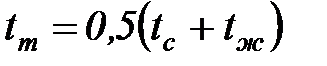 
.
Если теплоотдача направлена вверх, то результаты расчетов по формуле (124) необходимо увеличить на 30 %, если вниз – уменьшить на 30 %.
В практических расчетах для определения коэффициента теплоотдачи при свободной конвекции можно использовать уравнение (6) для тел любой формы и расположения в пространстве.
Теплообмен при свободной конвекции в ограниченном пространстве
В узких каналах и щелях восходящий (у нагретой поверхности) и нисходящий (у холодной) потоки взаимно затормаживаются и могут образововать несколько отдельных циркуляционных контуров (рис. 2).
а б в
| Рис. 2. Развитие свободной конвекции в ограниченном пространстве |
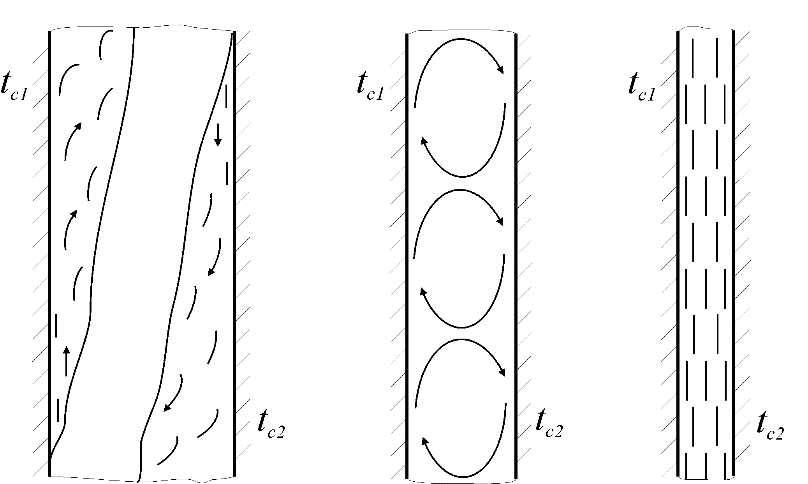
В вертикальных каналах, если расстояние между поверхностями велико, восходящее и нисходящее движение протекает без взаимных помех и имеет такой же характер, как и в неограниченном пространстве (рис. 2а).
|
|
|
Если же расстояние между поверхностями мало, то вследствие взаимных помех возникают внутренние циркуляционные контуры, высота которых определяется шириной щели, видом жидкости и интенсивностью процесса (рис. 2б).
Для упрощения расчетов переноса теплоты в ограниченном пространстве сложный процесс конвективного теплообмена заменяют эквивалентным процессом теплопроводности.
Тепловой поток, передаваемый через узкую щель, рассчитывают по закону Фурье. При этом коэффициент теплопроводности среды λ заменяется эквивалентным коэффициентом теплопроводностиλ э, который учитывает перенос теплоты теплопроводностью и конвекцией
. (7)
Коэффициент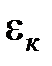 
в соотношении (7) определяется следующим образом:
при 
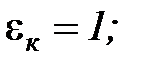
(8)
при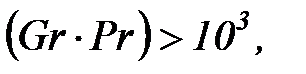 
.
В качестве определяющего линейного размера принимается толщина прослойки; определяющей температуры – средняя температура жидкости tж.
Для очень узких щелей (рис. 2в), в которых жидкость практически неподвижна, теплообмен осуществляется чистой теплопроводностью.
6. Теплообмен при вынужденном движении жидкости
По значению критерия Рейнольдса может быть определен режим течения жидкости - ламинарный, переходный или турбулентный.
Теплообмен при движении жидкости в трубе
При течении жидкости в трубах ламинарное движение наблюдается 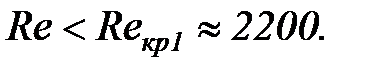при 
При 
возмущения потока необратимо нарушают ламинарный режим движения и способствуют турбулизации потока. Однако турбулентное движение устанавливается при 
При числах Рейнольдса от 
до 
движение жидкости является переходным от ламинарного к турбулентному.
Определяющим линейным размером при движении жидкости в трубах является внутренний диаметр трубы.
|
|
|
На рис. 10 схематично показано изменение скорости и температуры жидкости при течении в трубе. Здесь можно выделить начальный гидродинамический участок 1, где происходит образование пограничного слоя. Длина участка гидродинамической стабилизации увеличивается с ростом числа Re и уменьшается с усилением возмущения потока на входе в трубу.
При турбулентном течении распределение скорости имеет вид усеченной параболы 2 (рис. 3), форма которой зависит от значения числа Re. С увеличением значений критерия Рейнольдса наблюдается резкое изменение скорости вблизи стенки и ее пологое изменение в центральной части трубы.
Рис. 3. Развитие течения при вынужденном движении в трубе
Теплообмен в трубе существенно зависит от гидродинамической картины движения жидкости. В теплообмене участвует только пристенный пограничный слой, а остальная часть сечения, составляющая ядро потока, с температурой, равной температуре на оси, в теплообмене не участвует. До тех пор, пока тепловой пограничный слой не достигнет оси трубы, температура жидкости на оси трубы остается равной ее значению во входном сечении 3 (рис. 3). Изменение температуры на оси трубы вниз по потоку начинается с сечения, где тепловой пограничный слой достигает оси.
Длина участка тепловой стабилизации зависит от большого числа различных факторов, из которых главными факторами являются: число Рейнольдса, свойства жидкости, условия входа в трубу.
При ламинарном течении жидкости в трубах возможны два режима движения: вязкостный и вязкостно-гравитационный.
При вязкостном режиме силы вязкости преобладают над подъемными силами в жидкости. Такой режим наблюдается при ламинарном течении жидкостей с большой вязкостью в трубах малого диаметра и при малых температурных напорах.
При вязкостно-гравитационном режиме подъемные силы велики и заметное влияние на перенос теплоты оказывает свободная конвекция. На распределение скорости по сечению трубы значительное влияние оказывает изменение вязкости, а также интенсивность и направление свободного движения.
Вязкостный режим наблюдается при (Gr·Pr) < 8·105, средний коэффициент теплоотдачи при этом режиме определяется из уравнения
|
|
|
(9)
Формула действительна при 
; tс = idem и 
.
За определяющую температуру принята расчетная температура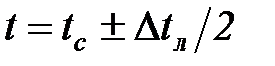 
(знак минус при нагревании и плюс при охлаждении); 
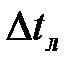– средний логарифмический температурный напор между поверхностью твердого тела и жидкостью.
Вязкостно-гравитационный режим имеет место при (Gr∙ Pr) > 8·105, средний коэффициент теплоотдачи в этом случае определяется по формуле
(10)
Значения среднего коэффициента теплоотдачи при переходном режиме движения можно рассчитать по формуле
Nu = (0, 563× Re0, 5 – 23, 346) ×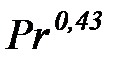 
Pr 0, 43 × 
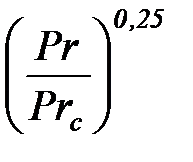. (11)
Для определения среднего коэффициента теплоотдачи при развитом турбулентном движении обычно используется формула М. А. Михеева
(12)
Формулы (10) – (12) действительны при l/d > 50; в них за определяющий линейный размер принят внутренний диаметр трубы; за определяющую температуру – средняя температура потока tж.
Если течение жидкости происходит по каналам некруглого сечения, то в качестве определяющего линейного размера принимается эквивалентный диаметр, определяемый по формуле dэ=4f/u, где f – площадь поперечного сечения канала (живое сечение); u – полный смоченный периметр канала.
Более интенсивно, чем в прямых трубах, процесс теплоотдачи протекает в изогнутых трубах (змеевиках). Для вычисления коэффициента теплоотдачи при турбулентном движении в змеевике можно использовать соотношение 
гдe α зм – коэффициент теплоотдачи в изогнутой трубе; α – коэффициент теплоотдачи в прямой трубе, вычисленный по формуле (12); d – диаметр трубы; R – радиус змеевика.
|
|
|
