 |
Теплообмен при поперечном обтекании труб жидкостью
|
|
|
|
Одиночные трубы. Теплообмен при поперечном обтеканиижидкостью трубы зависит от гидродинамической картины течения жидкости около поверхности (рис. 4. ). Обтекание трубы может быть плавным – безотрывным и отрывным. Плавное - безотрывное обтекание трубы наблюдается только при 
.
При Re> 5 пограничный слой, образующийся на передней части поверхности трубы, в кормовой части отрывается от поверхности; позади трубы образуются два симметричных вихря. В связи с этим коэффициент теплоотдачи меняется по периметру трубы.
В лобовой части коэффициент теплоотдачи имеет наибольшее значение при φ = 0, далее по периметру трубы α падает и достигает минимального значения в точке отрыва потока (точка а). В вихревой части коэффициент теплоотдачи увеличивается (рис. 4).
| Рис. 4. Схема движения и график изменения коэффициента теплоотдачи при поперечном обтекании трубы |
Для определения коэффициента теплоотдачи при поперечном обтекании одиночной трубы используют следующие уравнения подобия:
при Re = 5 ÷ 103 
(13)
при Re = 103 ÷ 2·105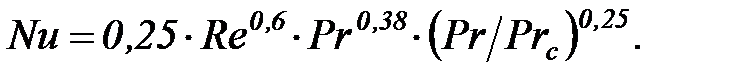 
(14)
За определяющий линейный размер принят внешний диаметр трубы; за определяющую температуру – температура набегающего потока; скорость жидкости отнесена к самому узкому сечению канала, в котором расположена труба.
Формулы (13) и (14) справедливы при условии, что угол между направлением потока и осью трубы, называемый углом атаки, равен 90º. При уменьшении угла атаки уменьшается интенсивность теплообмена и соответственно 
. Если угол атаки меньше 90º, то полученный коэффициент теплоотдачи необходимо умножить на поправочный коэффициент 
, приближенное значение которого можно определить по формуле
|
|
|
. (15)
Пучки труб. При поперечном обтекании потоком жидкости пучка труб интенсивность теплоотдачи зависит не только от факторов, влияющих на теплоотдачу одиночной трубы, но и от взаимного расположения труб в пучке, а также от плотности их расположения. Обычно применяют коридорное (по вершинам квадрата) и шахматное (по вершинам треугольника) расположение труб в пучке (рис. 5).
а б
Рис. 5. Схемы расположения труб в пучках:
а – шахматное; б – коридорное расположение
Плотность расположения труб в пучке характеризуется соотношениями между поперечным шагом S1, продольным шагом S2 и внешним диаметром труб d.
Исследованиями установлено, что коэффициент теплоотдачи на втором и третьем ряду труб выше, чем на первом ряду труб. Это объясняется увеличением турбулентности потока при прохождении его через пучок труб. Начиная с третьего ряда, поток практически стабилизируется, поэтому и коэффициент теплоотдачи для всех последующих рядов сохраняет постоянное значение. Если значение коэффициента теплоотдачи третьего ряда (и последующих рядов) α 3, то в коридорном пучке для первого и второго ряда труб коэффициент теплоотдачи α 1= 0, 6∙ α 3 и α 2 = 0, 9∙ α 3, а при шахматном расположении: α 1 = 0, 6∙ α 3 и α 2 = 0, 7∙ α 3.
Средний коэффициент теплоотдачи для третьего и последующих рядов определяется из уравнения подобия
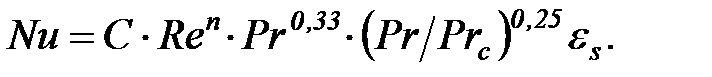(16)
Для шахматных пучков; С = 0, 41; n = 0, 6; для коридорных пучков:
С = 0, 26, n = 0, 65. Поправочный коэффициент ε s учитывает влияние относительных шагов. Для шахматного пучка: ε s = (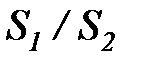 
)1/6 при 
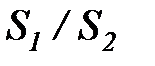< 2; и
ε s = 1, 12 при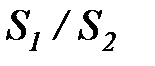 
≥ 2 ; для коридорного пучка ε s = ( 
)-0, 15.
Соотношение (16) рекомендуется использовать при Re =103 – 105. В качестве определяющего линейного размера принят наружный диаметр труб; в качестве определяющей температуры – средняя температура жидкости; скорость определяется в самом узком сечении пучка труб.
|
|
|
Среднее значение коэффициента теплоотдачи для всего пучка, состоящего из n рядов, можно найти из соотношения
, (17)
где F1 , F2, …, Fn – поверхности теплообмена в соответствующем ряду.
С учетом того, что F1 = F2 = F3, …, = Fn и α 3 = α 4= …= α n, соотношение (17) можно представить в виде
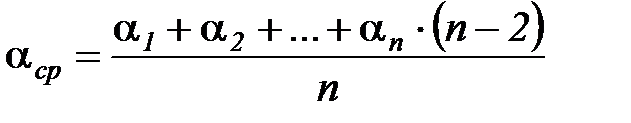. (18)
Принимая во внимание приближенные значения α 1 и α 2, получим следующие соотношения:
для коридорного пучка 
; (19)
для шахматного пучка 
. (20)
|
|
|
