ТЕМА 4. Полнодоступный пучок система с явными потерями. обслуживание простейшего потока вызовов модель m/m/v, к = v

ТЕМА 4. Полнодоступный пучок система с явными потерями. обслуживание простейшего потока вызовов модель m/m/v, к = v

 

 

Необходимые сведения по данной теме изложены в [1, стр. 50 - 58], [3, стр. 68 -84].

Контрольные вопросы

1. Дайте определение простейшего потока вызовов.

2. Что понимается под дисциплиной обслуживания - " явные потери"?

3. Как связан параметр простейшего потока вызовов с создаваемой ими нагрузкой?

4. Приведите первую формулу Эрланга. Дайте характеристику входящих в нее величин.

5. Как связаны между собой все виды потерь в данной модели обслуживания?

6. Как определяется нагрузка, обслуженная каждой линией пучка при упорядоченном и случайном режиме искания?

7. Охарактеризуйте область применения первой формулы Эрланга.

 

Пример решения задачи

задача

На однозвенную полнодоступную КС емкостью v = 10 линий поступает простейший поток вызовов с параметрами λ ₁= 180, λ ₂ = 300 вызовов в час. Среднее время обслуживания t = 90 сек. Вызовы обслуживаются в системе с явными потерями. Требуется определить:

Вероятность того, что в произвольный момент времени в системе занято точно i линий ( );

Среднее число занятых линий - М[i];

Построить графики зависимости P_i=f(i);

Потери по вызовам - Р_в, нагрузке - Р_н, времени - P_t;

Интенсивность нагрузки, обслуживаемой пучком линий.

решение

Вероятности Р, в данной модели определяются первой формулой Эрланга

,

где Y - интенсивность поступающей нагрузки, Y = λ t.

Определим величины Р_i для λ ₁ = 180 Выз/час. Для этого целесообразно воспользоваться рекуррентной формулой:

Поэтому сначала [можно провести расчет по первой формуле Эрланга] определяем вероятность занятости всех линий пучка , а далее по формуле (4. 1) все остальные значения P_i

Эрл

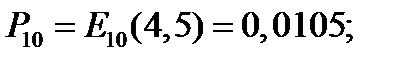
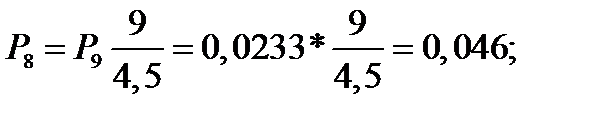
Аналогично:

Р₇ =0, 0828; P₆ =0, 128; Р₅ =0, 172; Р₄=0, 189; Р₃=0, 168; Р₂=0, 112; Р₁=0, 05; Р₀=0, 019;

 

Среднее число занятых линий:

,

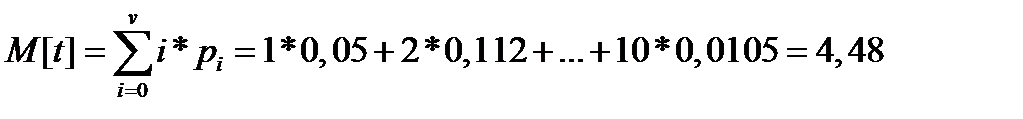т. е. чаще всего будут встречаться ситуации, когда в системе занято 4 или 5 линий.

Все виды потерь в этой модели равны между собой и равны P_v = Е_v( Y)

Р_в= Р_и=Р_t=Р_v=Е₁₀(4, 5)= 0, 0105 (10, 5%о).

Интенсивность обслуженной нагрузки:

Y₀=Y- Y_п=Y-YP_н= Y(1-P_н) = 4, 5 (1 -0, 0105)=4, 48 Эрл.

 На примере равенства M[i] = Y₀ пояснить смысл второго толкования телефонной нагрузки.

Аналогично проводятся расчеты при λ ₂ = 300. Для сравнения обе кривые зависимости Р_i= f(i) совместить на одном рисунке.

 

тема 5. Полнодоступный пучок система С явными потерями, обслуживание примитивного потока вызовов модель m/m/v, к = v, n

 

 

Перед решением задач рекомендуется изучить теоретический материал, изложенный в [1, стр. 69-76], [3, стр. 64-84].

Контрольные вопросы

1. Что понимается под примитивным потоком вызовов?

2. Как определяется параметр примитивного потока?

3. Приведите формулы Энгсета для вероятностей Р_i Р_в Р_и P_t.

4. Покажите, как из формулы Энгсета получить формулы Эрланга и Бернулли.

5. Приведите соотношение между вероятностями Р_в, Р_н, Р_t и P_v.

6. Поясните характер зависимости между интенсивностью поступающей нагрузки, емкостью пучка линий, числом источников нагрузки и вероятностью потерь.

7. Сравните пропускную способность полнодоступного пучка при простейшем и примитивном потоке вызовов. Проиллюстрируйте эту зависимость графически.

 

Пример решения задачи

ЗАДАЧА

Полнодоступный пучок из v=5 линий обслуживает поток вызовов. Определить нагрузку, которая может поступить на этот пучок при заданной вероятности потерь по вызовам Р_в = 5‰ в случае простейшего потока и примитивного потока от n₁=10 и n₂ =20 источников. По результатам решения задачи сделать выводы.

решение

В задаче предлагается сопоставить по пропускной способности при заданной вероятности потерь по вызовам - Р_в две модели обслуживания, которые характеризуются одинаковой дисциплиной обслуживания (явные потери), одинаковой структурой коммутационной системы (однозвенная), одинаковым способом объединения выходов групп коммутационных устройств (полнодоступные) и одинаковым законом распределения времени обслуживания вызовов (экспоненциальным). Отличие состоит только в классе входящего потока вызовов.

В случае простейшего потока, нагрузка, поступающая на КС при заданной емкости пучка и потерях определяем по таблицам [Приложение 2]. При v=5 и Р_в = 5‰.

Обслуженная нагрузка Y₀ = 1, 126 Эрл.

Процесс обслуживания примитивного потока однозвенным полнодоступным пучком в системе с явными потерями при экспоненциальном распределении времени обслуживания описывается формулой Энгсета. Для определения пропускной способности пучка целесообразно воспользоваться таблицами [13 или Приложением 3]. Откуда при n = 10, а =0, 15 Эрл:

Y= nа =10*0, 15 =1, 5 Эрл;

Y₀ = Y( 1 - 0, 005) = 1, 494 Эрл,

При n = 20 а = 0, 0642 Эрл;

Y= nа = 20*0, 0642 = 1, 284 Эрл;

Y₀= 1. 278 Эрл.

По результатам решения можно сделать следующие выводы:

Примитивный поток вызовов обслуживается лучше, чем простейший.

С увеличением числа источников нагрузки пропускная способность пучка уменьшается.

С увеличением числа источников нагрузки припускная способность пучка уменьшается, асимптотически стремясь при n → ∞ к пропускной способности простейшего потока.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: