 |
ТЕМА 8. Расчет пропускной способности многозвенных коммутационных схем
|
|
|
|
ТЕМА 8. Расчет пропускной способности многозвенных коммутационных схем
Необходимые сведения по теме содержатся в [1, стр. 147-172], [2, стр. 147-160], [3, стр. 128-149].
Контрольные вопросы
1. Перечислите методы расчета многозвенных коммутационных схем.
2. Дайте определение вероятностного графа применительно к звеньевой структуре.
3. Изобразите графы трех- и четырехзвенных схем в различных режимах искания.
4. Запишите выражения для потерь в параллельно-последовательном графе.
5. Поясните сущность методов КЛИГС и ППЛ для расчета многозвенных коммутационных схем.
6. В чем суть ограничений при определении доступности этими методами?
Пример решения задачи
ЗАДАЧА
Рассчитать вероятность внутренних блокировок в 4-х звеньевой коммутационной системе блочной структуры, работающей в режиме группового искания (Г). Задачу решить методом КЛИГС
Исходные данные:
1. ni=mi=8 (i= 
)- число входов (выходов) одного коммутатора на i-ом звене;
q=2 число выходов одного коммутатора последнего звена, которые объединяются в рассматриваемом направлении;
ki=8 (i= )- число коммутаторов на i-ом звене;
R =8 - число блоков в левой и правой части схемы;
α = 0, 6 Эрл - интенсивность нагрузки на один вход;
Yr=100 Эрл - интенсивность нагрузки поступающей на линии направления " r".
РЕШЕНИЕ
Определяем вторичные параметры схемы и нагрузку. Общее число входов N и выходов М схемы: 
Число линий в направлении г: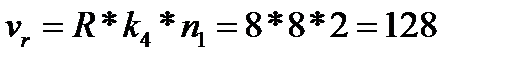 
Общая нагрузка, поступающая на все входы коммутационной системы Y=aN=0, 6*512=307, 2 Эрл.
Далее рассчитываем среднюю и максимальную доступность и среднюю недоступность исходной схемы.
Средняя доступность 
Максимальная доступность 
, где 
.
|
|
|
Следовательно, принимаем с учетом ограничения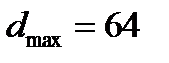 
.
Средняя недоступность 
Далее 4-х звеньевая исходная схема заменяется на однозвенную неполнодоступную схему с такой же пропускной способностью. Доступность этой схемы называется эффективной доступностью.
,
Где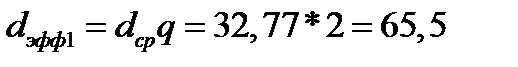 
;
Тогда 
Расчет однозвенной неполнодоступной схемы производим методом МПЯ. При этом учитывая, что Р< < 1, считаем Yф≈ Y
(или 1, 68‰)
ТЕМА 9. Расчет характеристик качества обслуживания в узкополосных цифровых сетях интегрального обслуживания (N-ISDN)
Необходимые сведения по теме содержатся в [19, 20].
Контрольные вопросы
1. Сформулируйте идею приближенного метода расчета потерь, распределенных систем обработки информации.
2. Дайте обоснование правомерности использования 1-ой формулы Эрланга в модели.
3. Какой класс входящих потоков предполагается в модели?
4. Проиллюстрируйте графически зависимость потерь от числа цифровых каналов для трех классов пользователей (В, 2В, 30В).
5. Поясните физический смысл понятия " нормированные средневзвешенные потери".
6. Приведите алгоритм расчета потерь и числа источников трех классов пользователей с помощью приближенного способа.
В предлагаемых задачах по данной теме используются следующие обозначения:
V - число стандартных цифровых каналов доступа (В) со скоростью 64 кБит/с;
n - число категорий источников вызовов;
Ai - параметр потока одного источника i-ой категории;
m i- число каналов, требующихся для обслуживания одного вызова i-ой категории;
hi - время обслуживания одного вызова (детерминированное) i-ой категории;
π - вероятность средних потерь для любого поступившего вызова;
π i- вероятность потерь для вызовов i-ой категории;
Ni -максимально допустимое число источников i-ой категории;
Ni' - относительная пропускная способность пучка для вызовов i-ой категории;
|
|
|
ki - числа, пропорциональные допустимому' числу источников i-ой категории (Ni);
х - коэффициент пропорциональности, определяемый из соотношения:
где
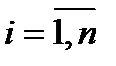- число категорий источников (вызовов);
А 1: А 2: А30- профиль трафика для доступов В1, В2, ВЗО - соответственно;
Ai - интенсивность нагрузки по вызовам для источников i-ой категории;
уi - интенсивность нагрузки на каналы для источников i-ой категории.
Пример решения задачи
ЗАДАЧА
Дано:
V = 30; n = 2;
A1 = 0, 2; A2 = 0, 1;
ml = 1; m2 = 4;
h1 =h2 = 1;
N1 =50; N2 = 25.
Определить: π -?; π 1 -?; π 2 -?.
РЕШЕНИЕ
1. Определяем общую нагрузку на каналы от источников двух категорий поформуле:
Эрл.
2. Дисперсия нагрузки:
Эрл2
3. Коэффициент скученности нагрузки:
Эрл.
4. Вероятность средних потерь для любого поступившего вызова определяется по формуле Хейворда с использованием таблиц Пальма:
5. Вероятность потерь вызовов для источников 1-ой и 2-ой категории соответственно:
‰;
‰
Из полученных результатов видно, что в наиболее " тяжелом" случае потери вызовов, требующие для обслуживания m2 = 4 канала не превышает 82, 2‰ Для вызовов, требующих для обслуживания ml = 1 канала, потери составляют 20, 5 ‰
|
|
|
