ТЕМА 6. Полнодоступный пучок. система с ожиданием. экспоненциальное время обслуживания вызовов простейшего потока. вторая формула Эрланга. модель M|M|V.

ТЕМА 6. Полнодоступный пучок. система с ожиданием. экспоненциальное время обслуживания вызовов простейшего потока. вторая формула Эрланга. модель M|M|V.

 

 

Необходимые сведения по теме содержатся в [1, стр. 79-88], [3, стр. 84-89].

Контрольные вопросы

1. Что представляет собой система обслуживания с ожиданием?

2. Назовите ограничение на величину поступающей нагрузки в системе с ожиданием?

3. Какие показатели качества обслуживания вызовов используются в системах с ожиданием?

4. Приведите вторую формулу Эрланга. От каких параметров зависят условные потери в этой модели?

5. Охарактеризуйте функцию распределения времени ожидания начала обслуживания.

6. Укажите рациональную область применения систем с ожиданием.

 

Пример решения задачи

задача

На полнодоступный пучок емкостью V=10 линий поступает простейший поток вызовов с параметром λ ₁=180^выз/_чac и λ ₂=300^выз/_чac. Время обслуживания распределено по экспоненциальному закону, средняя величина которого t = 90с. Постоянная обслуживания β =1. Допустимое время ожидания начала обслуживания t_∂ =90c. Требуется определить:

Вероятность потерь по времени – Р_t;

Вероятность занятия всех линий пучка - Р_у;

Вероятность потерь по вызовам - Р_в;

Вероятность того, что время ожидания начала обслуживания превысит t-P(γ > t);

Среднее время ожидания начала обслуживания по отношению к любому вызову М[γ ];

Среднее время ожидания начала обслуживания по отношению к задержанному вызову – M[γ _з];

Среднюю длину очереди - М[ j];

Вероятность того, что длина очереди превысит один вызов - P(j > 1).

решение

Вероятность потерь по времени - P_t можно определить по формуле

 

 

где Y - интенсивность поступающей нагрузки

 (Эрл)

 

 

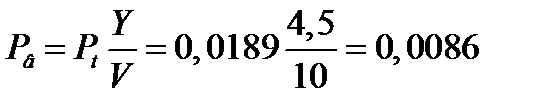
Значение функции распределения начала обслуживания Р(у > t) по формуле (5. 13) [1]:

,

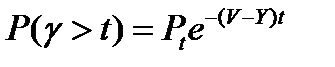где t - допустимое время ожидания начала обслуживания в относительных единицах

;

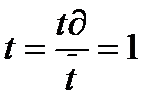Тогда 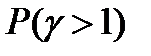 = 0, 0189е^{-(10-4, 5)} = 0, 000237= 0, 237 * 10^-3

Следовательно, из миллиона обслуженных вызовов 273 вызова будут ждать начала обслуживания время большее одной относительной единицы (90с).

Среднее время ожидания начала обслуживания в относительных единицах для любого вызова

;

В абсолютных единицах c.

Среднее время ожидания начала обслуживания в относительных единицах для задержанных вызовов

;

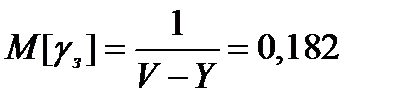В абсолютных единицах  с.

Средняя длина очереди

Вероятность того, что в очереди более n вызовов, определяется по формуле:

Тогда

Расчет характеристики системы обслуживания при λ ₂=300 ^выз/_час проводится аналогично. По результатам решения задачи провести сравнение показателей качества обслуживания при λ ₁=180 ^выз/_час и λ ₂=300 ^выз/_час.

 

ТЕМА 7. Полнодоступный пучок. Система с ожиданием. Постоянное время обслуживания вызовов простейшего потока. Теория Кроммелина. Формула Полячека-Хинчина модели M|D|V, M|D|1

 

 

Необходимые сведения по теме содержатся в [1] стр. 88-98, [2] стр. 175-180, [3] стр. 90-93.

Контрольные вопросы

1. В чем заключается сущность теории Кроммелина?

2. Сопоставьте характер распределения времени ожидания и пропускную способность систем с ожиданием для двух распределений длительности занятия: постоянного и показательного.

3. Приведите формулу Полячека-Хинчина и поясните физический смысл входящих в нее величин.

4. Преобразуйте формулу Полячека-Хинчина применительно к моделям М|М|1 иМР|1.

5. Проиллюстрируйте графически зависимость Р(у > t) = f(t) для модели обслуживания М|М|1 и M|D|1.

 

Пример решения задачи

ЗАДАЧА

На блок ГИ АТСКУ, обслуживаемый одним маркером (V=1), поступает нагрузка Y=40 Эрл. Средняя длительность занятия входа блока составляет t_вх=120с. Длительность обслуживания маркером одного вызова постоянна и составляет h = 0, 6с. Допустимое время ожидания начала обслуживания t_d=1, 2c. Определить:

Вероятность того, что вызов будет задержан Р(γ > 0);

Вероятность того, что время ожидания начала обслуживания превысит t-P(γ > t);

Среднее время ожидания начала обслуживания для любого вызова -М[γ ];

Среднее время ожидания начала обслуживания для задержанного вызова -М[γ _з];

 

РЕШЕНИЕ

Процесс обслуживания маркером поступающих вызовов можно рассматривать как математическую модель обслуживания простейшего потока однолинейным пучком, работающим по системе с ожиданием при случайной выборке вызовов из очереди. Эта модель исследована Берком и получены результаты в виде функции распределения времени ожидания Р(γ > t) в зависимости от нагрузки поступающей на маркер - η и допустимого времени ожидания начала обслуживания.

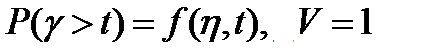
По полученной зависимости построены кривые (кривые Берка) [2, стр. 178 или Приложение 4]. Для определения величины η воспользуемся следующей формулой

Эрл.

Нагрузка, поступающая на маркер, меньше 1 Эрл, следовательно, маркер с обслуживанием такой нагрузки справится. Допустимое время ожидания выражается в относительных единицах:

 

 

По кривым Берка определяем Р(γ > 0) = 0, 2; Р(γ > 2) = 0, 002, т. е. 20% всех поступивших вызовов обслуживается с ожиданием; 0, 2% вызовов обслуживаются с временем ожидания свыше 1, 2 с.

Среднее время ожидания начала обслуживания определяется по формуле Полячека-Хинчина. Применительно к данной модели они имеют следующий вид:

; ;

Тогда эта величина в относительных единицах:

; ;

В абсолютных единицах М[γ ] = 0, 125 · 0, 6 = 0, 075 с;

М[γ ₃] = 0, 625 · 0, 6 = 0, 375 с.

Такое время ожидания начала обслуживания для абонента является вполне приемлемым.

 

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: