 |
тема 10. Измерение и распределение нагрузки и потерь в сетях связи 2 страница
|
|
|
|
 (11. 16)
(11. 16)
Пример расчета распределенной и остаточной емкости сети при загрузке 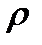 = 0, 1:
= 0, 1:

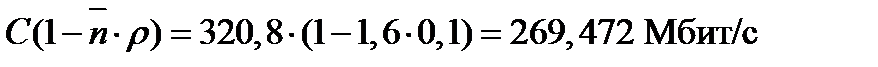
Результаты расчета общей распределенной и остаточной емкостей сети для ряда коэффициентов загрузки 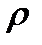 , равных 0, 1; 0, 2; 0, 3; …. 0, 9 приведены в таблице 11. 12.
, равных 0, 1; 0, 2; 0, 3; …. 0, 9 приведены в таблице 11. 12.
Таблица 11. 12– Распределенная и остаточная емкость сети при различной загрузке
| P | 0, 1 | 0, 2 | 0, 3 | 0, 4 | 0, 5 | 0, 6 | 0, 7 | 0, 8 | 0, 9 |
| C, Mбит/с | 320, 8 | 160, 4 | 106, 93 | 80, 2 | 64, 16 | 53, 47 | 45, 83 | 40, 1 | 35, 64 |
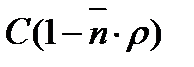 , Mбит/с , Mбит/с
| 269, 48 | 109, 1 | 55, 60 | 28, 87 | 12, 83 | 2, 14 | -5, 5 | -11, 23 | -15, 68 |
На основании полученных данных рассчитаем по формуле (11. 15) распределение общей емкости по каналам сети.
Пример расчета емкости сети в первом канале при загрузке 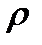 = 0, 1:
= 0, 1:
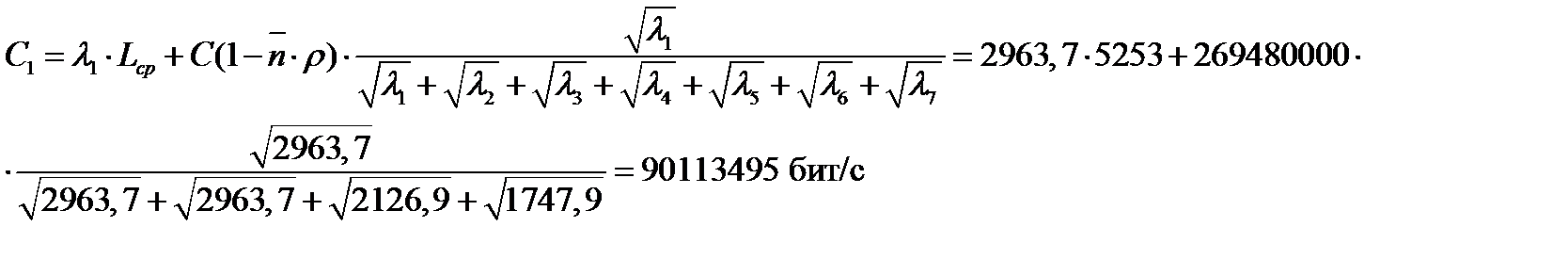
Результаты расчета приведены в таблице 11. 13.
Таблица 11. 13 – Распределение общей емкости сети по каналам
| p | 0, 1 | 0, 2 | 0, 3 | 0, 4 | 0, 5 | 0, 6 | |
| Емкость канал, Мбит/с | 90, 113 | 45, 748 | 30, 95 | 23, 554 | 19, 117 | 16, 16 | |
| 90, 113 | 45, 748 | 30, 95 | 23, 554 | 19, 117 | 16, 16 | ||
| 74, 323 | 36, 739 | 24, 202 | 17, 938 | 14, 179 | 11, 674 | ||
| 66, 43 | 32, 359 | 20, 993 | 15, 315 | 11, 907 | 9, 636 |
Для выбора необходимой емкости для каждого канала, требуется определить время задержки распространения пакетов в каналах и в сети в целом при различных коэффициентах загрузки. Данный расчет осуществляется по следующим формулам:
 (11. 17)
(11. 17)
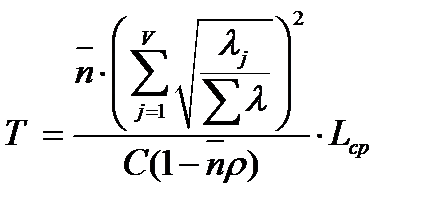 (11. 18)
(11. 18)
Пример расчета времени задержки распространения пакетов в первом канале и в сети в целом при загрузке 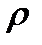 = 0, 1:
= 0, 1:


Результаты расчетов приведены в таблице 11. 14.
Таблица 11. 14 – Время задержки распространения пакетов в каналах в секундах
|
|
|
| p | 0, 1 | 0, 2 | 0, 3 | 0, 4 | 0, 5 | 0, 6 | |
| Задержка в канале, с | 0, 00007047 | 0, 00017406 | 0, 0003415 | 0, 0006578 | 0, 00148 | 0, 008874 | |
| 0, 00007047 | 0, 00017406 | 0, 0003415 | 0, 0006578 | 0, 00148 | 0, 008874 | ||
| 0, 00008318 | 0, 00020546 | 0, 0004032 | 0, 0007764 | 0, 001747 | 0, 010475 | ||
| 0, 00009176 | 0, 00022665 | 0, 0004447 | 0, 0008565 | 0, 001927 | 0, 011555 | ||
| В сети | 0, 00007859 | 0, 00019413 | 0, 0003809 | 0, 0007336 | 0, 001651 | 0, 009897 | |
Критерием выбора значения требуемой емкости для того или иного канала является максимально допустимое время задержки, определяемое используемыми в сети службами. Из рассмотренных в проекте служб, наиболее критичной к данному параметру является IP-телефония. Требования к каналам службы IP-телефонии зависят от используемого кодека голосового сигнала. В настоящее время наибольшее распространение получили кодеки G. 711, G. 729A, G. 723. 1. Их параметры приведены в таблице 11. 15.
Таблица 11. 15 – Параметры голосовых кодеков IP-телефонии.
| Тип кодека | Метод | Сложность алгоритма | Битовая скорость, Кбит/с | Размер отсчёта, байт | Длит. отсчёта, мс | Вносимая задержка, мс | Полоса пропускания, Кбит/с |
| G. 711 | PCM A-law | Средняя | 87, 2 | ||||
| G. 729A | CS-ACELP | Средняя | 31, 2 | ||||
| G. 723. 1 | MP-MLQ | Высокая | 6, 3 | 21, 9 | |||
| G. 723. 1 | ACELP | Высокая | 5, 3 | 20, 8 |
Из приведенных данных видно, что наиболее требовательным к полосе пропускания канала и задержке прохождения пакетов является кодек G. 711. Задержка передачи пакетов в сети для данного кодека не должна превышать 80 мс. При использовании других кодеков, требования к каналу будут меньше. Реальная задержка передачи пакетов IP-телефонии будет еще ниже, за счет поддержки всем коммуникационным оборудованием стандартов QoS, обеспечивающих приоритезацию голосового трафика, и меньшим размеров самих голосовых пакетов.
Рисунок 2 – Распределение трафика службы FTP
Рисунок 3 – Распределение трафика службы IP
|
|
|
Рисунок 4 – Распределение трафика службы IP АТС
2 ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ.
Курсовая работа состоит из одиннадцати задач. Перед выполнением каждой задачи необходимо изучить ту часть курса, которая относится к этой задаче.
Задача 1. На коммутационную систему поступает примитивный и простейший потоки вызовов с параметром от одного свободного источника α выз/час. Определить вероятность поступления ровно К вызовов Рk на единичном интервале времени (t=1), (k=0, 1, 2... N) при числе источников нагрузки N. Значения N и а приведены в таблице 2. 1.
Таблица 2. 1
| Номер варианта | ||||||||||||
| α, выз/час | 0, 6 | 0, 62 | 0, 64 | 0, 66 | 0, 68 | 0, 7 | 0, 6 | 0, 62 | 0, 64 | 0, 65 | 0, 68 | 0, 7 |
| N |
| Номер варианта | ||||||||||||
| α, выз/час | 0, 72 | 0, 65 | 0, 63 | 0, 61 | 0, 64 | 0, 69 | 0, 71 | 0, 61 | 0, 63 | 0, 65 | 0, 67 | 0, 69 |
| N |
| Номер варианта | |||||||
| α, выз/час | 0, 72 | 0, 65 | 0, 63 | 0, 61 | 0, 64 | 0, 69 | 0, 71 |
| N |
Задача 2. Цифровая станция DX-200 обслуживает 1000-ю абонентскую группу АТС. Рассчитать поступающую на цифровую станцию нагрузку, если известен структурный состав 1000-ой группы: Nки, и Nнх, среднее число вызовов от одного абонента С, среднее время разговора Т, доля вызовов закончившихся разговором Рр. Значения Nки, Nнх, и Рр приведены в таблице 2. 2. Значения Ски=1, 14 выз/час, Снх=4 выз/час, Тки=110 с, Тнх=85 с
Таблица 2. 2
| Номер варианта | |||||||||||
| Nки | |||||||||||
| Nнх | |||||||||||
| Р ‰ | 0, 5 | 0, 55 | 0, 6 | 0, 65 | 0, 7 | 0, 5 | 0, 55 | 0, 6 | 0, 65 | 0, 7 | 0, 5 |
| Номер варианта | |||||||||||
| Nки | |||||||||||
| Nнх | |||||||||||
| Р ‰ | 0, 55 | 0, 6 | 0, 5 | 0, 55 | 0, 6 | 0, 65 | 0, 7 | 0, 5 | 0, 55 | 0, 6 | 0, 65 |
| Номер варианта | |||||||||
| Nки | |||||||||
| Nнх | |||||||||
| Р ‰ | 0, 7 | 0, 6 | 0, 65 | 0, 7 | 0, 5 | 0, 55 | 0, 6 | 0, 65 | 0, 7 |
Задача 3. Рассчитать величину возникающей на цифровой АТС нагрузки от абонентов следующих категорий:
Индивидуального пользования Nu; народно - хозяйственного сектора " делового" Nнд; народно -хозяйственного сектора " спального" Nнс; таксофонов местной связи Nт. мест. ; таксофонов междугородных (исходящая связь) Nт. межд. ; районных переговорных пунктов (РПП) Nрпп; исходящих СП от УАТС (на правах абонентов)Nсл; факсимильных аппаратов (соединения по телефонному алгоритму) Nф; абонентов ЦСИО с числом доступов: типа 2B+D и 30B+D.
|
|
|
При определении возникающей нагрузки следует учесть нагрузку на ЗСЛ и УСС. Нумерация на сети шестизначная. Значения Nu, Nнд, Nнс, Nт. мест, Nт. межд, Nрпп, Nсл, Nф, 2B+D и 30B+D приведены в таблице 2. 3.
Таблица 2. 3
| Номер варианта | ||||||||||
| Nu | ||||||||||
| Nнд | ||||||||||
| Nнс | ||||||||||
| Nт. мест | ||||||||||
| Nт. межд | ||||||||||
| Nрпп | ||||||||||
| Nсл | ||||||||||
| Nф | ||||||||||
| 2B+D | ||||||||||
| 30B+D |
| Номер варианта | |||||||||||
| Nu | |||||||||||
| Nнд | |||||||||||
| Nнс | |||||||||||
| Nт. мест | |||||||||||
| Nт. межд | |||||||||||
| Nрпп | |||||||||||
| Nсл | |||||||||||
| Nф | |||||||||||
| 2B+D | |||||||||||
| 30B+D |
| Номер варианта | ||||||||||
| Nu | ||||||||||
| Nнд | ||||||||||
| Nнс | ||||||||||
| Nт. мест | ||||||||||
| Nт. межд | ||||||||||
| Nрпп | ||||||||||
| Nсл | ||||||||||
| Nф | ||||||||||
| 2B+D | ||||||||||
| 30B+D |
Задача 4. На однозвенную полнодоступную КС емкостью V линий поступает простейший поток вызовов с параметрами λ 1, λ 2 вызовов в час. Среднее время обслуживания t сек. Вызовы обслуживаются в системе с явными потерями. Значения V, λ 1 и λ 2 приведены в таблице 2. 4. Требуется определить:
Вероятность того, что в произвольный момент времени в системе занято точно i линий (  );
);
Среднее число занятых линий - М[i];
Построить графики зависимости Pi=f(i);
Потери по вызовам - Рв, нагрузке - Рн, времени - Pt;
Интенсивность нагрузки, обслуживаемой пучком линий.
|
|
|
Таблица 2. 4
| Номер варианта | ||||||||||||
| V | ||||||||||||
| λ 1, вызовов в час | ||||||||||||
| λ 2, вызовов в час | ||||||||||||
| t, c |
| Номер варианта | ||||||||||||
| V | ||||||||||||
| λ 1, вызовов в час | ||||||||||||
| λ 2, вызовов в час | ||||||||||||
| t, c |
| Номер варианта | |||||||
| V | |||||||
| λ 1, вызовов в час | |||||||
| λ 2, вызовов в час | |||||||
| t, c |
Задача 5. Полнодоступный пучок из V линий обслуживает поток вызовов. Определить нагрузку, которая может поступить на этот пучок при заданной вероятности потерь по вызовам Рв‰ в случае простейшего потока и примитивного потока от n1 и n2 источников. Значения V, Рв, n1 и n2 приведены в таблице 2. 5. По результатам решения задачи сделать выводы.
Таблица 2. 5
| Номер варианта | |||||||||||
| V | |||||||||||
| Рв‰ | |||||||||||
| n1 | |||||||||||
| n2 |
| Номер варианта | |||||||||||
| V | |||||||||||
| Рв‰ | |||||||||||
| n1 | |||||||||||
| n2 |
| Номер варианта | |||||||||
| V | |||||||||
| Рв‰ | |||||||||
| n1 | |||||||||
| n2 |
Задача 6. На полнодоступный пучок емкостью V линий поступает простейший поток вызовов с параметром λ 1выз/чac и λ 2выз/чac. Время обслуживания распределено по экспоненциальному закону, средняя величина которого t с. Постоянная обслуживания β =1. Допустимое время ожидания начала обслуживания t∂ c. Значения V, λ 1, λ 2, t и t∂ приведены в таблице 2. 6. Требуется определить:
Вероятность потерь по времени – Рt;
Вероятность занятия всех линий пучка - Ру;
Вероятность потерь по вызовам - Рв;
Вероятность того, что время ожидания начала обслуживания превысит t-P(γ > t);
Среднее время ожидания начала обслуживания по отношению к любому вызову М[γ ];
Среднее время ожидания начала обслуживания по отношению к задержанному вызову – M[γ з];
Среднюю длину очереди - М[ j];
Вероятность того, что длина очереди превысит один вызов - P(j > 1).
Таблица 2. 6
| Номер варианта | |||||||||||
| V | |||||||||||
| λ 1, вызовов в час | |||||||||||
| λ 2, вызовов в час | |||||||||||
| t, c | |||||||||||
| t∂ , c |
| Номер варианта | |||||||||||
| V | |||||||||||
| λ 1, вызовов в час | |||||||||||
| λ 2, вызовов в час | |||||||||||
| t, c | |||||||||||
| t∂ , c |
|
|
|
| Номер варианта | |||||||||
| V | |||||||||
| λ 1, вызовов в час | |||||||||
| λ 2, вызовов в час | |||||||||
| t, c | |||||||||
| t∂ , c |
|
|
|


