Рис. 2.1. Распределение Гаусса

Геометрически величина σ совпадает с расстоянием от  до точек перегиба кривой f(x) Гаусса, т. е. в точках x= ±σ функция плотности имеет точки перегиба, в которых кривая меняется с выпуклой на вогнутую.

Графическая интерпретация связи между этими величинами имеет тот смысл, что для распределения Гаусса не зависимо от значений параметров  и σ площадь под кривой составляет:

0, 68	для интервала	±σ;
0, 95	для интервала	±1, 96σ;
0, 99	для интервала	±2, 58σ;
0, 9974	для интервала	±3σ.

Широкое применение распределения Гаусса на практике объясняется тем фактом, что при нормальном распределении случайных величин, вероятность попадания значений за пределы довольно узкого интервала, с границами ±3σ, составляет всего 0, 0026, т. е. менее 0, 3 %.

Использование распределения Гаусса и его свойств позволяет обрабатывать результаты санитарно-экологических наблюдений и за состоянием здоровья населения и за состоянием окружающей среды, определять степень их взаимосвязи и оценивать достоверность полученных                                результатов.

На основе полученных данных в соответствии с формулами 1. 1 – 1. 26, приведёнными в работе 1 «Расчёт показателей заболеваемости взрослого населения», производится расчёт тех показателей, для расчёта которых имеются соответствующие данные, например: суммарный показатель заболеваемости, доля (удельный вес) различных форм и групп болезней и структура заболеваемости, число детей с врождёнными аномалиями, число посещений по поводу заболеваний и др.

Итак, мы вычислили ряд показателей. Теперь надо убедиться, что они не случайны и отражают реальную картину состояния заболеваемости, другими словами, надо убедиться в их достоверности. Оценка достоверности полученных показателей осуществляется с использованием методов статистической обработки.

Для любого полученного показателя, прежде всего, необходимо вычислить стандартную среднюю ошибку. Стандартную среднюю ошибку m вычисляют по формуле (2. 5):

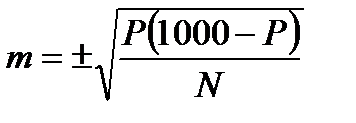,                                               (2. 5)

где m –величина стандартной средней ошибки; P– показатель заболеваемости;  N – число наблюдений.

Следует обратить внимание на то, что формула (2. 5) справедлива только для значений P< 1 000.

Если величина утроенной стандартной средней ошибки превышает величину показателя заболеваемости, то такой показатель считают статистически не достоверным и он исключается из дальнейшей обработки.

Для оценки достоверности различия сравниваемых показателей заболеваемости по выбранным территориям или когортами используют критерий Стьюдента-Фишера.

При использовании этого критерия оценка достоверности производится по формуле (2. 6):

,                                                        (2. 6)

где: t – коэффициент достоверности; P₁ и P₂ – показатели заболеваемости в первой и второй когортах; m₁ и m₂ – стандартная средняя ошибка в первой и второй когортах.

В табл. 2. 4 приведены значения коэффициентов достоверности и доверительного интервала. Значения коэффициента достоверности t сравнивают с табличным значением (табл. 2. 4).

В большинстве случаев в медицинской практике, также как и в практике биологических и экологических исследований считают результаты приемлемо точными, если они попадают в доверительный интервал 0, 95. Это означает, что истинное значение изучаемого параметра с вероятностью 95 % находится в его пределах.