 |
Таблица 2.9. Результаты анализа образцов воды на содержание свинца. 95– ю процентиль определим, используя формулу, отбросив при этом последнее 50– е значение ряда, как «аномальное»
|
|
|
|
Таблица 2. 9
Результаты анализа образцов воды на содержание свинца
| № пробы | Pb мг/кг | № пробы | Pb мг/кг | № пробы | Pb мг/кг | № пробы | Pb мг/кг | № пробы | Pb мг/кг |
| 0, 17 | 0, 23 | 0, 34 | 1. 28 | ||||||
| 0, 17 | 0, 23. | 0, 41 | 1, 39 | ||||||
| 0, 18 | 0, 24 | 0, 44 | 1, 62 | ||||||
| 0, 19 | 0, 24 | 0, 47 | 1, 80 | ||||||
| 0, 05 | 0, 21 | 0, 24 | 0, 48 | 2, 19 | |||||
| 0, 05 | 0, 21 | 0, 25 | 0, 70 | 2, 21 | |||||
| 0, 1 | 0, 21 | 0, 28 | 0, 74 | 2, 41 | |||||
| 0, 1 | 0, 21 | 0, 30 | 0, 76 | 2, 63 | |||||
| 0, 1 | 0, 22 | 0, 31 | 0, 77 | 2, 76 | |||||
| 0, 1 | 0, 22 | 0, 32 | 0, 80 | 27, 80 |
Разобьём вариационный ряд на 5 интервалов в соответствии с уровнями превышения. Результаты поместим в табл. 2. 10.
95– ю процентиль определим, используя формулу, отбросив при этом последнее 50– е значение ряда, как «аномальное».
В нашем примере вариационный ряд содержит 50 проб.
95– й уровень =  = 47, 5.
= 47, 5.
Таблица 2. 10
Группировка загрязнения воды по величине превышения
концентрации свинца над ПДК
| Величина превышения концентраций | Количество анализов | Середина интервала, xi | Накопленные | Плотность распределения в интервале,
| ||
| Единиц mi | % или частость, wi | Частоты, Fi | Частости, pi | |||
| От 0 до 1, 0 | 0, 5 | |||||
| 1, 1– 2, 0 | 1, 55 | 8, 89 | ||||
| 2, 1– 3, 0 | 2, 55 | 31, 1 | ||||
| 3, 1– 5, 0 | 4, 05 | 7, 36 | ||||
| > 5, 0 | – | – | ||||
| Итого: | – | – | ||||
Полученное число округляем до целого, таким образом 47– я проба будет нижней границей 95– го процентиля. Величина 95– го процентиля будет:
 = 2, 41 + 0, 35
= 2, 41 + 0, 35 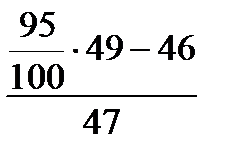 = 2, 421.
= 2, 421.
Характеристиками вариационного ряда являются: являются дисперсия и среднее квадратическое отклонение.
|
|
|
Дисперсию называют мерой вариации вариационного ряда. Дисперсию для не сгруппированного ряда вычисляют по формуле:
 , (2. 18)
, (2. 18)
Для сгруппированного ряда дисперсию вычисляют по формуле:
 , (2. 19)
, (2. 19)
Среднее квадратическое отклонение измеряется в тех же единицах, что и варьируемый признак, и исчисляется путём извлечения квадратного корня из дисперсии:
для несгруппированных данных:
 , (2. 20)
, (2. 20)
для сгруппированных данных:
 , (2. 21)
, (2. 21)
Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются конкретные варианты признака от его среднего значения. Отклонение, выраженное в σ , называется нормированным или стандартизованным.
Обоснование наличия взаимосвязи между показателями состояния здоровья и вредными факторами
При изучении влияния факторов окружающей среды на здоровье населения не достаточно убедиться в достоверности полученных данных, как по оценке здоровья населения, так и по оценке самих вредных факторов. Одной из самых трудных задач является доказательство того, что влияние изучаемого фактора на здоровье населения, на появление того или иного заболевания, на самом деле существует. В числе методов, используемых для доказательства, можно упомянуть экспертные оценки, графоаналитические методы и статистические методы, включающие также вероятностный анализ. Нисколько не сомневаясь в полезности и экспертных оценок и графоаналитических методов, мы не станем задерживать на них внимания в силу ограниченного объёма данного пособия и остановимся лишь на статистических методах, поскольку они при всех допущениях всё же дают какие то количественные оценки. При хорошем владении и знании возможностей, с помощью этих методов можно получить вполне достоверные и убедительные доказательства существования влияния того или иного фактора на определённый вид заболеваемости населения. Тем более что эти методы в настоящее время достаточно хорошо компьютеризированы. Мы остановим наше внимание лишь на основных понятиях статистических методов, которые, тем не менее, должны дать основы для понимания существа и возможностей применения таких методов.
|
|
|
При анализе причинно-следственных связей между факторами воздействия и показателями состояния здоровья наиболее часто используется корреляционно регрессионный метод.
Корреляция характеризует степень взаимосвязи между вариационными рядами. Степень и характер взаимосвязи между двумя корреляционными рядами x и y определяет коэффициент корреляции rxy, который вычисляется по формуле:
 , (2. 22)
, (2. 22)
где: rxy – коэффициент корреляции между параметрами x и y; xi и yi– значение параметров x и y в i– м наблюдении;  и
и  – средние арифметические значения параметров x и y для n проведенных опытов или наблюдений.
– средние арифметические значения параметров x и y для n проведенных опытов или наблюдений.
Величина коэффициента корреляции всегда находится в пределах
– 1  rxy
rxy  +1. (2. 23)
+1. (2. 23)
Если rxy=0, то это означает, что параметры x и y совершенно не зависимы друг от друга. Если rxy< 0, то это означает, что с увеличением в вариационном ряду наблюдаемых величин x соответствующие им значения величин y уменьшаются, т. е. между вариационными рядами существует обратная взаимосвязь.
Если rxy=1, то это означает, что между параметрами x и y существует прямо пропорциональная функциональная зависимость. Если rxy> 0, то с увеличением в вариационном ряду наблюдаемых величин x соответствующие им значения величин y увеличиваются, т. е. между вариационными рядами существует прямая взаимосвязь.
Чем больше абсолютная величина коэффициента корреляции, тем больше доверительная вероятность наличия взаимосвязи между исследуемыми явлениями.
Поскольку и показатели загрязнения окружающей среды и показатели здоровья населения являются величинами случайными и показатели загрязнения не зависят от здоровья, полагают, что они подчиняются закону распределения Гаусса. Для распределения Гаусса все случайные величины укладываются с доверительной вероятностью 0, 99 в интервал 3σ.
|
|
|
Среднеквадратическое отклонение σ для нормального распределения определяют по формуле (2. 20).
Для распределения Гаусса доверительный интервал коэффициента r корреляции определяют через доверительный интервал коэффициента z. Коэффициент r корреляции связан с коэффициентом z соотношением:
 . (2. 24)
. (2. 24)
Среднюю ошибку mr коэффициента корреляции рассчитывают по формуле:
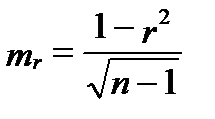 , (2. 25)
, (2. 25)
Если между показателем состояния здоровья и исследуемыми факторами загрязнения окружающей среды действительно существует взаимосвязь и это подтверждается с одной стороны достоверностью определения самих показателей и факторов, и с другой большим значением коэффициента корреляции, то можно говорить не только и наличии взаимосвязи, но и о существовании функциональной связи.
Для описания такой связи предложена математическая модель в виде уравнения регрессии (2. 26):

 , (2. 26)
, (2. 26)
где  – теоретическое значение (математическое ожидание) показателя состояния здоровья; b0 – фоновое значение показателя состояния здоровья; n– число данных о величинах исследуемого фактора состояния окружающей среды; Xi, – исследуемый вредный фактор (загрязнитель окружающей среды: физический, химический или биологический), обуславливающий изменение показателя состояния здоровья на исследуемой территории; bi – коэффициент регрессии, характеризующий силу и направленность влияния вредного фактора.
– теоретическое значение (математическое ожидание) показателя состояния здоровья; b0 – фоновое значение показателя состояния здоровья; n– число данных о величинах исследуемого фактора состояния окружающей среды; Xi, – исследуемый вредный фактор (загрязнитель окружающей среды: физический, химический или биологический), обуславливающий изменение показателя состояния здоровья на исследуемой территории; bi – коэффициент регрессии, характеризующий силу и направленность влияния вредного фактора.
В уравнении (2. 26) первая сумма характеризует линейное влияние вредных факторов, вторая сумма – нелинейность зависимости, если такая имеет место.
В наиболее простом случае, когда между одним вредным фактором и одним показателем здоровья существует взаимосвязь, т. е. когда при увеличении величины фактора показатель здоровья увеличивается или уменьшается пропорционально изменению фактора, эта взаимосвязь может быть выражена функциональным уравнением:
|
|
|
 . (2. 27)
. (2. 27)
Коэффициент b линейной регрессии и коэффициент rxy корреляции связаны между собой уравнением:
 , (2. 28)
, (2. 28)
где σ ч и σ н – соответственно среднеквадратические отклонения показателя x здоровья и вредного фактора y, которые определяют по формулам:
 , (2. 29)
, (2. 29)
 , (2. 30)
, (2. 30)
где xi и yi – текущие значения величин x и y в каждом опыте,  и
и  – средние арифметические значения величин x и y.
– средние арифметические значения величин x и y.
До сих пор мы рассматривали лишь вопрос о взаимосвязи одного показателя здоровья и одного вредного фактора. На самом деле реальная ситуация требует анализа влияния нескольких вредных факторов на ряд показателей здоровья. В таких случаях пользуются уравнениями множественной регрессии.
В случае линейных зависимостей уравнение множественной регрессии принимает вид:
 = a0+a1x1+a2x2+…+anxn , (2. 31)
= a0+a1x1+a2x2+…+anxn , (2. 31)
где a1, a2,.... an – вредные факторы, влияющие на показатель здоровья.
На практике для решения этой задачи требуется определить множество величин для каждого вредного фактора и величины коэффициентов множественной регрессии. Для решения уравнения множественной регрессии используют метод наименьших квадратов. Для решения такой задачи необходимо составить систему из n+1 уравнений, т. е. число наблюдений должно быть на 1 больше числа анализируемых признаков. При рассмотрении взаимосвязи более чем между двумя признаками, находят коэффициенты множественной регрессии. Отличие коэффициента множественной регрессии состоит в том, что он всегда положителен и его величина лежит в пределах от 0 до 1.
В настоящее время для корреляционно регрессионного анализа, в том числе и для решения задач оценки воздействия вредных факторов на показатели здоровья населения разработаны хорошие компьютерные программы типа SAS, STATISTIСA и др.
|
|
|



