 |
Таблица 2.5. Данные по школе «А». Данные по школе «В». Данные по школе «В» Возрастная группа, лет Число учащихся, чел
|
|
|
|
Таблица 2. 5
Данные по школе «А»
| Возрастная группа, лет | Число учащихся, чел. | Число заболеваний физич. недостатками | Заболеваемость (число учащихся с физич. откл) на 1000 | Стандарт, человек | Ожидаемое число больных в группе стандарта |
| 6 – 14 | |||||
| 15 – 19 | 77, 52 | ||||
| Всего: | 251, 94 |
Распространённостьзаболеваний среди детей (заболеваемость) рассчитываем на 1 000 детей в соответствии с формулой (1. 11). Данные расчёта помещаем в 4– м столбце.
Таблица 2. 6
Данные по школе «В»
| Возрастная группа, лет | Число учащихся, чел. | Число заболеваний физич. недостатками | Заболеваемость (число учащихся с физич. откл) на 1000 | Стандарт, человек | Ожидаемое число больных в группе стандарта |
| 6 – 14 | 64, 29 | 109, 29 | |||
| 15 – 19 | 112, 5 | 57, 37 | |||
| Всего: | 73, 77 | 154, 91 |
За стандарт можно принять общую численность населения двух исследуемых групп или численность населения одной из изучаемых групп данного возрастного состава, или численность населения какой-либо третьей группы.
Мы принимаем за стандарт суммарную численность учащихся обеих школ и данные по численности стандарта помещаем в пятом столбце.
Далее составляется простая пропорция: в школе «А» в возрастной группе 6 – 14 лет заболеваемость составляет 64, 26 на 100 человек. Сколько было бы больных в этой возрастной группе при численности учащихся равной стандарту 1700 человек:
1000 – 4, 29
1700 – х (2. 11)
откуда  .
.
По аналогии рассчитываем стандартизованные показатели для других возрастных групп и для всех учащихся по обеим школам и помещаем данные в шестом столбце.
|
|
|
Сравнивая ожидаемые числа больных в группах стандарта, обнаруживаем, что в школе «В» заболеваемость учащихся была бы гораздо меньше по сравнению со школой «А».
При анализе когорт населения, проживающих на разных территориях, можно разбить всё население на такие возрастные категории, в которых заболеваемость примерно одинакова, например: 15 – 19 лет, 20 – 29, 30 – 39, 40 – 49, 50 – 59, 60 лет и старше.
Анализ вариационных рядов и определение процентиле
При исследовании проб на загрязнение объектов окружающей среды, также как и при исследовании заболеваемости населения, сопоставлении показателей с помощью статистических методов часто используют вариационные ряды.
Совокупность некоторых данных состоит из отдельных данных – единиц изучаемой совокупности. Единицы изучаемой совокупности обладают интересующим нас признаком в разной мере. Для каждой единицы совокупности данный признак принимает различные значения, т. е. имеет некоторую вариацию (Теория статистики, 2000).
Вариацией признака называется наличие различий в численных значениях признаков у отдельных единиц совокупности.
Для выявления характера распределения единиц совокупности по варьирующим признакам, определения закономерностей этого распределения, строят ряды распределения единиц совокупностей по какому– либо варьирующему признаку.
Ряды распределения, построенные по количественному признаку, называются вариационными.
Вариационные ряды по способу построения бывают двух видов: дискретные и интервальные.
Дискретный ряд распределения можно рассматривать как такое преобразование ранжированного (упорядоченного) ряда, при котором перечисляются отдельные значения признака и указывается их частота или частость.
По своей конструкции дискретный вариационный ряд состоит из двух столбцов: один столбец – значения варьирующего признака (x – варианты), другой – частоты (m – абсолютное число случаев данного варианта) или частости (w – относительная доля каждой частоты в общей сумме частот).
|
|
|
Для построения вариационного ряда значения признака ранжируют в порядке возрастания или в порядке убывания.
Общая схема вариационного ряда такова: в совокупности, состоящей из N единиц, некоторая переменная величина xi (т. е. какой– то варьирующий признак) принимает различные значения, а каждое из этих значений имеет частоту mi, или частость wi (табл. 2. 7).
Таблица 2. 7
Общий вид дискретного вариационного ряда
| Вариант xi | Частота mi | Частость wi |
| x1 | m1 | w1 |
| x2 | m2 | w2 |
| . . . | . . . | . . . |
| xn | mn | wn |
| Итого: | 
| 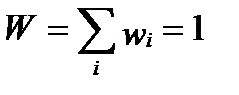
|
Приведённая схема вариационного ряда применяется для тех случаев, когда варьирующий признак принимает небольшое количество значений. Если же вариантов много, то невозможно образовать группы для каждого из них.
Примером дискретного ряда может служить распределение домашних хозяйств по числу членов семьи, представленное в табл. 2. 8.
Если число вариантов велико или признак имеет непрерывную вариацию, то объединение отдельных наблюдений в группы производят на базе интервала. Интервал – это такая группа, которая имеет определенные пределы значений варьирующего признака. Эти пределы обозначают двумя числами, которые указывают верхнюю и нижнюю границы интервала. При использовании интервалов образуются интервальные ряды распределения. Строя интервальный вариационный ряд, определяют, прежде всего, число групп, на которое хотят разбить всю совокупность.
|
|
|


