 |
Таблица 2.4. Значения коэффициента достоверности
|
|
|
|
Таблица 2. 4
Значения коэффициента достоверности
| Коэффициент достоверности t | 1, 28 | 1, 65 | 1, 96 | 2, 58 | 3, 03 | |
| Доверительный интервал, α | 0, 68 | 0, 8 | 0, 9 | 0, 95 | 0, 99 | 0, 999 |
| Доверительная вероятность, p | 0, 32 | 0, 20 | 0, 10 | 0, 05 | 0, 01 | 0, 001 |
Пример 1. На территории «А» с повышенным загрязнением атмосферного воздуха в течение 1 года диагностировано заболевание бронхиальной астмой у 1 527 мужчин, при общей численности мужского населения 8 760 человек. На контрольной территории «В» расположенной в зелёной зоне число мужчин, заболевших астмой в течение того же года составило 518, при численности мужского населения 7 780 человек. Необходимо определить суммарные показатели заболеваемости для территории «А» и зоны «В», оценить достоверность данных по каждой зоне и достоверность различия полученных показателей.
Показатель суммарной заболеваемости мужчин на территории «А» в соответствии с формулой (1. 7) из работы 1:
на 1 000 мужчин.
Стандартная средняя ошибка для территории «А» в соответствии с формулой (2. 5):
mA=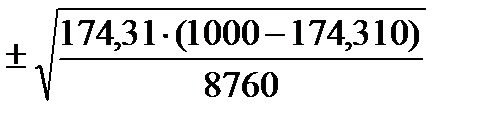 
=3, 72
Показатель суммарной заболеваемости мужчин на территории «А» в соответствии с формулой (1. 7):
на 1000 мужчин.
Стандартная средняя ошибка для территории «А» в соответствии с формулой (2. 5):
mB = 
=2, 82.
Утроенное значение стандартной средней ошибки не превышает показателя заболеваемости ни в первом, ни во втором случаях, так что данные по заболеваемости можно считать достоверными.
Достоверность различия сравниваемых показателей заболеваемости по выбранным территориям проверяем с помощью критерия Стьюдента– Фишера, используя формулу (2. 6):
= 25, 17.
Величина коэффициента достоверности намного превышает значения, приведённые в табл. 2. 4, что подтверждает различие между показателями заболеваемости на сравниваемых территориях.
|
|
|
Часто возникает вопрос о том, какое минимальное число наблюдений (случаев заболевания, больных пациентов и т. п. ) необходимо иметь, чтобы получить оценку с допустимой точностью, например, с ошибкой ±5 % или ±10 %. Чаще всего требуется определить показатели с ошибкой ±5 %.
Предельную ошибку показателя определяют по формуле (2. 7):
, (2. 7)
где Δ – ошибка показателя; t – коэффициент достоверности; P –величина показателя в % или относительных единицах; q=(1– P) или q=(100– P) в зависимости от того, в каких величинах определён показатель; n – число наблюдений.
Чтобы получить результат с 95 %– м доверительным интервалом (см. табл. 2. 4), коэффициент достоверности t принимают равным 2.
Тогда из формулы (2. 7) можно найти величину числа n наблюдений (2. 8):
. (2. 8)
Пример 2. По данным медицинского пункта школы в течение года за медицинской помощью обратились 90 % учеников. Какова должна быть минимальная численность группы наблюдения, чтобы оценка заболеваемости имела ошибку ±5 %?
В соответствии с формулой получим:
n= 
= 144.
Т. е., для получения показателя о заболеваемости с погрешностью ±5 % необходимо иметь группу учащихся не менее 144 человек.
Если численность населения, проживающего на изучаемой территории известна, то для расчёта необходимого числа наблюдений используют формулу (2. 9):
. (2. 10)
Расчёт стандартизованных показателей
Существенное влияние на уровень и структуру заболеваний оказывают не только факторы окружающей среды, но и состав населения: возраст, пол, группы повышенного риска, к которым обычно относят стариков, детей и беременных женщин. При сопоставлении заболеваемости по наблюдаемым территориям для исключения влияния структуры населения применяют метод стандартизации. Стандартизованные показатели, рассчитанные по данному методу, показывают, какими были бы показатели заболеваемости сравниваемых групп, если бы они имели одинаковый возрастной и половой состав.
|
|
|
Расчёт стандартизованных коэффициентов рассмотрим на простом примере.
Пример 3. Сравнить показатели заболеваемости по физическим недостаткам (искривление позвоночника, плоскостопие, и др. ) учащихся двух школ. Данные о численности учащихся по возрастным группам в школе «А» и в школе «В» приведены в таблицах 2. 5 и 2. 6.
|
|
|
