 |
Полная система уравнений электрических цепей
|
|
|
|
Законы Кирхгофа применительно к графу схемы или электрической цепи характеризуют систему в целом без учета характеристик ее элементов. Матричные уравнения
Ai =- A Á (или Di =- D Á) и Cu = Ce (3.10)
определяют систему из р отдельных уравнений. Такая система недостаточна для описания процессов в электрических цепях, так как не известны р токов и р напряжений.
Чтобы дополнить систему уравнений, необходимо определить (или задать) еще р уравнений. Эти уравнения должны отражать свойства элементов системы – ветвей электрической цепи. Очевидно, что такие связи должны быть записаны для р ветвей цепи. В матричной форме запишем эти уравнения в виде
i = f (u) или u = j (i),
т.е.
(3.11)
В зависимости от характера функций fk и j k (k =1… р) системы уравнений электрических цепей могут быть линейными – для линейных электрических цепей, т.е. для цепей, у которых r, L, С и М не зависят от значений и направлений токов и напряжений в цепи, и нелинейными – для нелинейных электрических цепей, т.е. для цепей, у которых r, L, С или М хотя бы одного из участков зависят от значений или от направлений токов и напряжений в этом участке цепи.
Каждая ветвь линейной цепи может содержать сопротивление, индуктивность, емкость, идеальный источник ЭДС и идеальный источник тока (рис. 3.9).
Рис. 3.9
Ток в сопротивлении ветви 
и падение напряжения ветви U связаны законом Ома.
U = Z × I,
где сопротивление ветви 
. Эти соотношения для всех ветвей можно записать в матричной форме:
или кратко
U = Z × I, (3.12)
где Z – диагональная матрица сопротивлений ветвей;
U, I, J, E – соответственно векторы напряжений и токов ветвей, токов источников тока и ЭДС ветвей.
|
|
|
Это матричная форма закона Ома.
Замечание: Матрица Z диагональна лишь в случае, когда ток k -ой ветви создает напряжение на сопротивлении Z, k -ой ветви. В цепях со взаимной индукцией Z имеет элементы вне главной диагонали Zij = Zji = ± sMij.
М -сопротивления индуктивной связи i -ой и j -ой ветвей. Они положительны (отрицательны), если ориентация i -ой и j -ой ветвей по отношению одноименных зажимов одинакова (противоположна).
Уравнения закона Ома можно представить в другой форме:
I = Y × U, (3.13)
где Y = Z - 1 – матрица проводимостей, обратная матрице сопротивлений ветвей.
Если в функции fk и j k входят производные токов и напряжений, то процессы в этой линейной или нелинейной электрической цепи будут характеризоваться системой, соответственно, линейных или нелинейных дифференциальных уравнений. При отсутствии производных в функциях fk и j k процессы в этой линейной или нелинейной электрической цепи будут характеризоваться системой, соответственно, линейных или нелинейных алгебраических уравнений.
Система из 2 р уравнений, включающая в себя уравнения, записанные согласно законам Кирхгофа, и уравнения, характеризующие связи между токами и напряжениями элементов электрической цепи, и есть полная система уравнений электрической цепи, или полная математическая модель этой цепи.
Узловые уравнения
Для формирования системы уравнений относительно узловых напряжений выразим 
через параметры пассивных и активных элементов обобщенных ветвей:
.
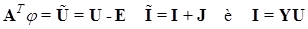Согласно первому закону Кирхгофа, для узлов графа
AI =- AJ или AYU =- AJ.
Теперь напряжение на ветвях определим через узловые потенциалы:
U = A T × j +Е.
Таким образом, получаются уравнения
AY × A T × j = AJ - AY × E, (3.14)
|
|
|
которые называют узловыми уравнениями.
Если ввести обозначения
– Y y = AY × AT – матрица узловых проводимостей,
– J y = AJ - AY × E – матрица узловых токов,
то узловые уравнения запишутся кратко:
Yy j = Jy. (3.14a)
При выполнении узлового анализа на ЭВМ обычно не строятся матрицы A и Y и не выполняют матричные умножения, а непосредственно пользуются правилами составления узловых уравнений:
1. Диагональные элементы матрицы Y у положительны и Yjj равны сумме проводимостей ветвей, подключенных к j -муузлу.
2. Внедиагональные элементы матрицы Yy отрицательны и Yjk равны сумме проводимостей ветвей, включенных между j -м и k -м узлами.
3. Произвольный элемент вектора тока Jy с номером jJ j равны суммеузловых токов, втекающих в j -узел.
Тогда l-я ветвь, направленная от узла j к узлу k, приводит к следующему вкладу в матрицы Yy и Jy:
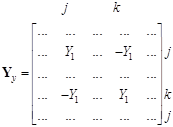
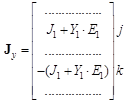
Так составляются уравнения по методу узловых потенциалов последовательным перебором топологического списка ветвей схемы.
Потенциалы узлов j k равны напряжениям Vk между q -1 узлом и опорным узлом.
Контурные уравнения
Уравнения на основе второго закона Кирхгофа
CU = CE,
уравнение закона Ома
U = Z × I
и соотношение
подставим в контурное уравнение и получим:
.
Токи в обобщенных ветвях определим через контурные токи:
.
Так получаются контурные уравнения:
. (3.15)
Если ввести обозначения
Zk =С Z × С T – матрица контурных сопротивлений,
Ek = С E -С Z × J – матрица контурных ЭДС, то контурные уравнения запишутся в виде:
. (3.15а)
В матричной форме решения для контурных токов
(3.16)
выражают принцип наложения.
|
|
|
